Derive Modified Gram Schmidt QR Decomposition Algorithm from Gram Schmidt Orthogonalisation (part 2)

Posted 2020-10-26 cxxszz

All rights reserved. Please don‘t share this article without notifying me. Email address: [email protected]

From eq. 10 in part 1 we can find the Classical Gram Schmidt Algorithm, which is numerically unstable or sensitive to perturbation:

Q=zeros((m,n))
R=zeros((n,n))
for k= 1 to n
    tmpk=cAk
    for i= 1 to k-1
        R[i][k]=cAk^T*cQi
        tmpk=tmpk-R[i][k]*cQi
    R[k][k]=||tmpk||
    cQk=tmpk/R[k][k]

Q calculated by Classical Gram Schmidt algorithm is not very orthogonal due to rounding errors. An example is provided by X. Jiao[1]

 

　　

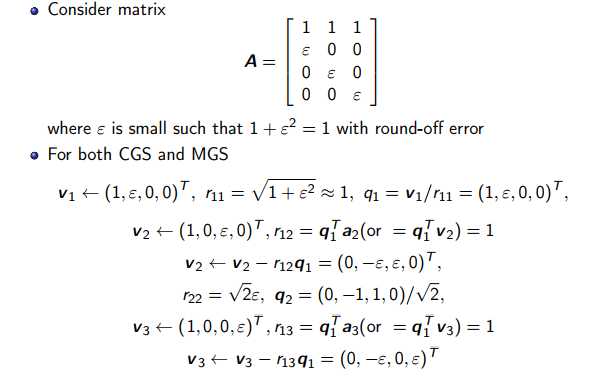
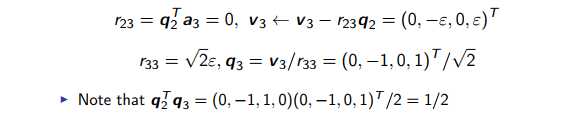
The error introduced in q1 also cause errors in q2 and q3. We will discuss how to avoid this in the next part.

[1] http://www.ams.sunysb.edu/~jiao/teaching/ams526_fall11/lectures/lecture06.pdf