这个问题我是在PAT大区赛题里遇见的。题目如下:
多项式A除以B(25 分)
这仍然是一道关于A/B的题,只不过A和B都换成了多项式。你需要计算两个多项式相除的商Q和余R,其中R的阶数必须小于B的阶数。
输入格式:
输入分两行,每行给出一个非零多项式,先给出A,再给出B。每行的格式如下:
N e[1] c[1] ... e[N] c[N]
其中N是该多项式非零项的个数,e[i]是第i个非零项的指数,c[i]是第i个非零项的系数。各项按照指数递减的顺序给出,保证所有指数是各不相同的非负整数,所有系数是非零整数,所有整数在整型范围内。
输出格式:
分两行先后输出商和余,输出格式与输入格式相同,输出的系数保留小数点后1位。同行数字间以1个空格分隔,行首尾不得有多余空格。注意:零多项式是一个特殊多项式,对应输出为0 0 0.0。但非零多项式不能输出零系数(包括舍入后为0.0)的项。在样例中,余多项式其实有常数项-1/27,但因其舍入后为0.0,故不输出。
输入样例:
4 4 1 2 -3 1 -1 0 -1
3 2 3 1 -2 0 1
输出样例:
3 2 0.3 1 0.2 0 -1.0 1 1 -3.1
题目的意思很明确,就是要求 anxn+an-1xn-1+an-2xn-2+。。。+a1x1+a0x0 除以amxm+am-1xm-1+am-2xm-2+。。。+a1x1+a0x0 的商和余数。这可以类比多项式除法进行。
这题的样例数据可表示为:x4-3x2-x-1 除以 3x2-2x+1 求其的商和余数。
手工计算步骤就是下图所示:
依次乘一个(1/3)x2,(2/9)x,(-26/27),很明显就是想办法消掉最高次项,知道所剩的余项最高次小于除数的最高次。
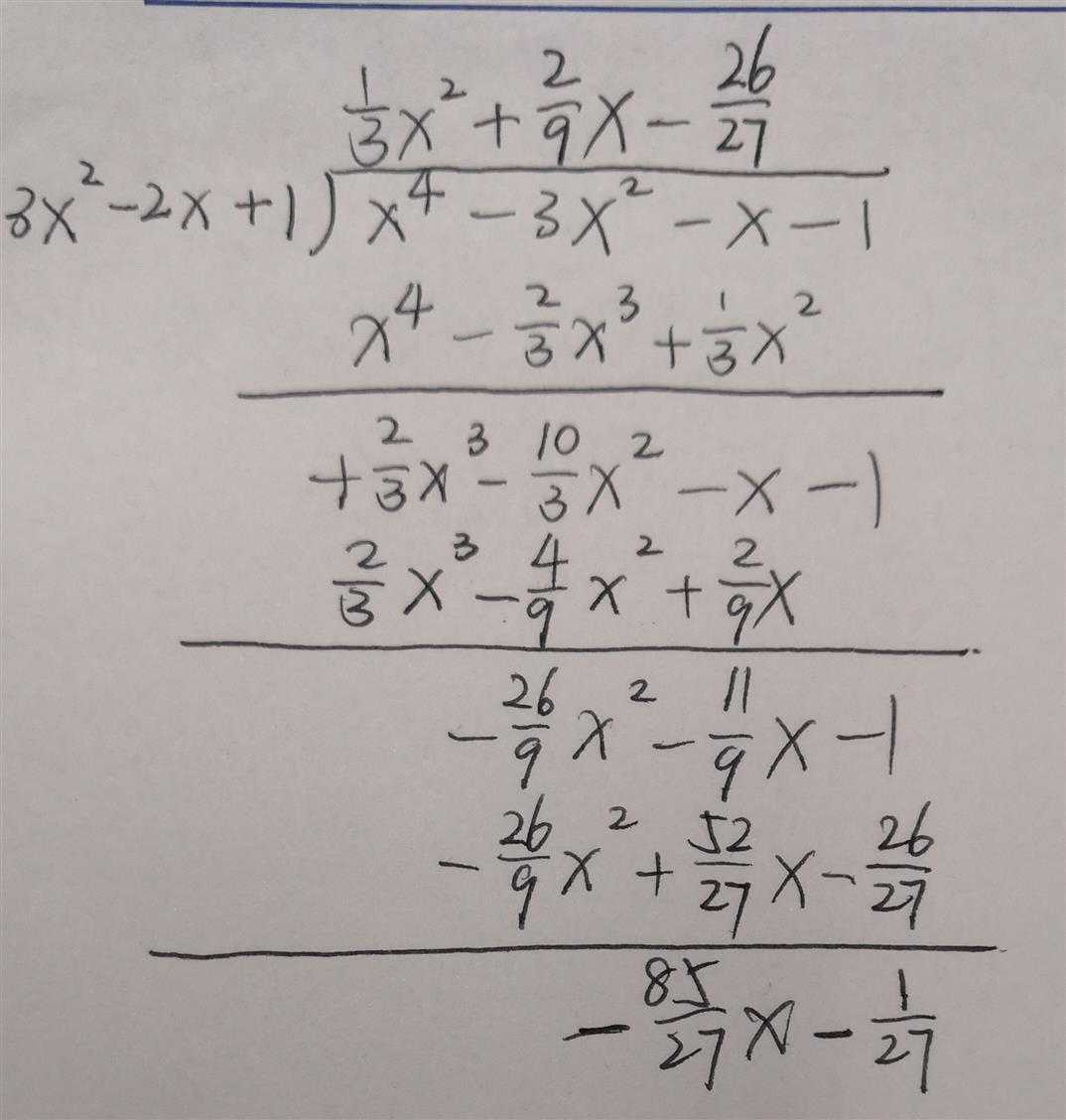
分数化简后就为答案。(上方为商,下方为余数)。
算法核心部分上面已经讲了,接下来讲一下数据结构的设置。
因为每一项都是指数、系数这两个变量,所以我们可以用STL中的map来存储这一个<指数,系数>键值对。
因此我在此设了三个map数组
map<int,double> a; //多项式A(最后的余数) map<int,double> b; //除数 map<int,double> c; //商
多项式A的初始化
1 cin>>lena; //A多项式的项数 2 for(int i=0;i<lena;i++){ 3 int e; 4 double c; 5 cin>e; 6 cin>>c; 7 maxe_a = max(maxe_a,e);//找到A的最高次指数 8 a[e] = a[e] + c; //相同系数即刻合并 9 }
多项式B同理,但要注意多求一个最小项次数。
接下来,最重要的来了,那就是除法运算的过程。首先我们先知道要进行几次除法的运算。由上面的示例步骤我们可以知道,运算次数为:( A的最高次幂 - B的最高次幂 )+ 1 次,也可理解为( i = max (eA); i >= max(eB); i --)这样的过程。
商的其中一项就是(当前A的最高次幂系数 / B的最高次幂系数)这是系数,指数为 (当前A的最高次幂 - B的最高次幂),为什么加一个当前呢?因为A每次最高项都会被(B的最高次项 * 相应商的一项)所消掉,直至A最终变为要求的余数项为止。
余数项,就是A每一项每次被 (B的每项 * 相应项的商)做差后系数没被削成0的项。
1 for(int i = maxe_a;i>=maxe_b;i--){ 2 if(b[maxe_b]!=0){ 3 div = 1.0*a[i]/b[maxe_b]; 4 //printf("div=%.1lf\\n",div); 5 sub = i - maxe_b; 6 c[sub] = div; 7 maxe_c = max(maxe_c,sub); //求商的最高次幂 8 //每次从剩余项的最高次开始,直到B的最低次,每项做差 9 for(int j=i;j>=mine_b;j--){ 10 if(j-sub >= 0){ 11 a[j] = a[j] - b[j-sub]*c[sub]; 12 } 13 } 14 } 15 }
之后c[ ] 就是商,a[ ] 就是余数项。
最后依据题意,为c[ ]数组 a[ ]数组做下四舍五入。接下来讲一下怎么做四舍五入。
因为题目要求保留一位有效数字,所以就先把这个数*10化为(int)+/-0.5,再除以10即可。今后碰见四舍五入问题一次类推!
for(int i=maxe_c;i>=0;i--){ //四舍五入处理 c[i] = (double)((int)(c[i]*10 + (c[i]<0?-0.5:0.5)))/10; if(c[i]){ cnt++; } }
最后奉上此题解的原码:

1 #include<cstdio> 2 #include<iostream> 3 #include<map> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 8 map<int,double> a; 9 map<int,double> b; 10 map<int,double> c; 11 int lena,lenb; 12 13 int main(){ 14 int maxe_a = 0,mine_b=32767,maxe_b=0,maxe_c=0; 15 double div; 16 int sub; 17 cin>>lena; 18 for(int i=0;i<lena;i++){ 19 int e; 20 double c; 21 cin>>e; 22 cin>>c; 23 maxe_a = max(maxe_a,e); //找到A的最高次指数 24 a[e] = a[e] + c; //相同系数即刻合并 25 } 26 cin>>lenb; 27 for(int i=0;i<lenb;i++){ 28 int e; 29 double c; 30 cin>>e; 31 cin>>c; 32 mine_b = min(mine_b,e); //找到B的最低次指数 33 maxe_b = max(maxe_b,e); //找到B的最高次指数 34 b[e] = b[e] + c; //相同系数即刻合并 35 } 36 for(int i = maxe_a;i>=maxe_b;i--){ 37 if(b[maxe_b]!=0){ 38 div = 1.0*a[i]/b[maxe_b]; 39 //printf("div=%.1lf\\n",div); 40 sub = i - maxe_b; 41 c[sub] = div; 42 maxe_c = max(maxe_c,sub); //求商的最高次幂 43 for(int j=i;j>=mine_b;j--){ //每次从剩余项的最高次开始,直到B的最低次,每项做差 44 if(j-sub >= 0){ 45 a[j] = a[j] - b[j-sub]*c[sub]; 46 } 47 } 48 } 49 } 50 int cnt=0; 51 for(int i=maxe_c;i>=0;i--){ 52 c[i] = (double)((int)(c[i]*10 + (c[i]<0?-0.5:0.5)))/10;//四舍五入处理 53 if(c[i]){ 54 cnt++; 55 } 56 } 57 if(cnt ==0){ 58 printf("0 0 0.0\\n"); 59 }else{ 60 printf("%d",cnt); 61 for(int i=maxe_c;i>=0;i--){ 62 if(c[i]){ 63 printf(" %d %.1lf",i,c[i]); 64 } 65 } 66 printf("\\n"); 67 } 68 cnt =0; 69 for(int i = maxe_a;i>=0;i--){ 70 a[i] = (double)((int)(a[i]*10 + (a[i]<0?-0.5:0.5)))/10;//四舍五入处理 71 if(a[i]){ 72 cnt++; 73 } 74 } 75 if(cnt ==0){ 76 printf("0 0 0.0"); 77 }else{ 78 printf("%d",cnt); 79 for(int i=maxe_a;i>=0;i--){ 80 if(a[i]){ 81 printf(" %d %.1lf",i,a[i]); 82 } 83 } 84 } 85 return 0; 86 }
最后总结一下,像这题可以作为多项式相除的模板题目。以后还可用于多项式的因式分解,求方程根等问题。
