序言
你可能早早就听说过这个故事:
在一家超市里,有一个有趣的现象:尿布和啤酒赫然摆在一起出售。但是这个奇怪的举措却使尿布和啤酒的销量双双增加了。这不是一个笑话,而是发生在美国沃尔玛连锁店超市的真实案例,并一直为商家所津津乐道。沃尔玛拥有世界上最大的数据仓库系统,为了能够准确了解顾客在其门店的购买习惯,沃尔玛对其顾客的购物行为进行购物篮分析,想知道顾客经常一起购买的商品有哪些。沃尔玛数据仓库里集中了其各门店的详细原始交易数据。在这些原始交易数据的基础上,沃尔玛利用数据挖掘方法对这些数据进行分析和挖掘。一个意外的发现是:"跟尿布一起购买最多的商品竟是啤酒!经过大量实际调查和分析,揭示了一个隐藏在"尿布与啤酒"背后的美国人的一种行为模式:在美国,一些年轻的父亲下班后经常要到超市去买婴儿尿布,而他们中有30%~40%的人同时也为自己买一些啤酒。产生这一现象的原因是:美国的太太们常叮嘱她们的丈夫下班后为小孩买尿布,而丈夫们在买尿布后又随手带回了他们喜欢的啤酒。
这背后的知识,简单来说,就是下面要讲的内容~
正文
从大规模数据集中寻找物品间的隐含关系被称作关联分析(association analysis)或者关联规则学习(association rule learning)。这里的主要问题在于,寻找物品的不同组合是一项十分耗时的任务,所需的计算代价很高,蛮力搜索方法并不能解决这个问题,所以需要用更智能的方法在合理的时间范围内找到频繁项集。
关联分析是在大规模数据集中寻找有趣关系的任务。这些关系可以有两种形式:
- 频繁项集
- 关联规则
频繁项集(frequent item sets)是经常出现在一块儿的物品的集合,
关联规则(association rules)暗示两种物品之间可能存在很强的关系。
借用一个《机器学习实战》里的例子:
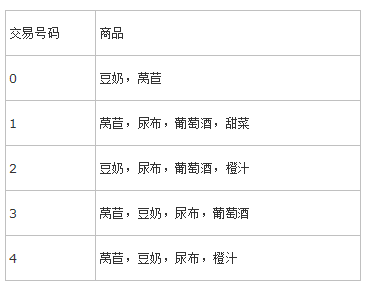
比如说 {尿布,豆奶} 就是一个频繁项集,因为这个组合在例子中经常出现;
然后我们从这个频繁项集出发分析,是不是买尿布的人就经常也买豆奶呢?
就得出了一个: 尿布 \(\rightarrow\) 豆奶 这样一个关联规则,或者
豆奶 \(\rightarrow\) 尿布, 但是两者不等价,后面会说
再来两个概念 支持度(support) 和 可信度(confidence)
支持度:数据集中包含该项集的记录所占的比例
可信度:比如有两个集合 P,H; 则关联规则P \(\rightarrow\) H 的可信度为: \(\frac{support(P \cup H)}{support(P)}\)
举几个简单的例子:
- {尿布,豆奶} 的 support 为 3/5,因为在 5 个交易中,{尿布,豆奶} 的组合出现了 3 次
- 那如果我们求 尿布 \(\rightarrow\) 豆奶 的 confidence 就是 \(\frac{support(\{尿布,豆奶\})}{support(\{尿布\})}=\frac{3/5}{4/5}=\frac{3}{4}\)
- 那么豆奶 \(\rightarrow\) 尿布 的 confidence 就是 \(\frac{support(\{尿布,豆奶\})}{support(\{豆奶\})}=\frac{3/5}{4/5}=\frac{3}{4}\) ,...还是 3/4 ,很不幸的巧合,但是我们还是可以看出来,其实计算过程是不一样的
Apriori原理
频繁项集
支持度和可信度是用来量化关联分析是否成功的方法,假设想找到支持度大于 0.8 的所有项集,应该如何去做?一个办法是生成一个物品所有可能组合的清单,然后对每一种组合统计它出现的频繁程度,但是当物品数量成千上万时,上述做法非常慢
我们可以这么想:
如果一个项集是频繁的, 那么它的所有子集也都是频繁的;
接着:如果一个项集是非频繁的,那么它的所有超集也都是非频繁的。
这条结论就在于,之前我们说,列出所有可能的组合很麻烦,有了这个结论,我们如果找到一些非频繁项集,那么他们的超集就可以全部不用考虑了,这样就简化了很大一部分计算;这就是 Apriori原理
基于这样的思想,我们可以设计一个这样的算法,目标就是找到 support 大于等于一个阈值的所有频繁项集;
那么
Input: 最小support, 数据集
Output: 满足条件的所有频繁项集
主体思想就是:我们先算比较小的集合的support(最小就是单个元素的集合), 把计算过程中不满足support的集合去掉,以留下来的集合和元素组合成新的集合,然后继续筛选,直到留下的项集都满足最小support,返回结果。
所以我们可以看到核心部分就是,如何在一轮迭代之后生成新的数据集;因为每次迭代,我们的频繁项集的元素个数都只加1,那么,我们生成新的候选的频繁项集的方法就是:用上一轮的项集中只相差1个元素的集合的并集作为新一轮候选的频繁项集。
关联规则
根据上述内容,规则就是出现一些物品,能够依此推出另一些物品出现的可能性。也即上述内容中所说的confidence(可信度)
那么其实挖掘关联规则也就是找到confidence 大于等于一个阈值的所有关联规则;
在这里也借助Apriori算法的思想:如果某条规则并不满足最小可信度要求,那么该规则的所有子集也不会满足最小可信度要求。
那么在上面的那句话中,怎么理解一条规则的子集?
假设项集为 {0,1,2,3},假设 0,1,2 -> 3 的 confidence 不满足最小可信度的要求,那么任意前件(条件)为 {0,1,2} 的子集,后件(结果)包含 3 的关联规则的 confidence 都不满足要求;就比如 0,1 -> 3 和 1,2 -> 0,3 都不会满足要求;
基于上面的思想,我们可以这样生成关联规则:
初始有 \(n\) 个元素,我们可以生成 \(n\) 个初始关联规则(分离出一个元素做后件,其余做前件);
然后对每个关联规则一次算confidence, 筛去不符合条件的规则;
然后对留下的关联规则再次分离元素做后件,生成新的一轮的规则,再进行筛选。
这样呢,每次只让后件的元素个数加 1,可以有效快速的剪枝
我们可以看如下这幅图:
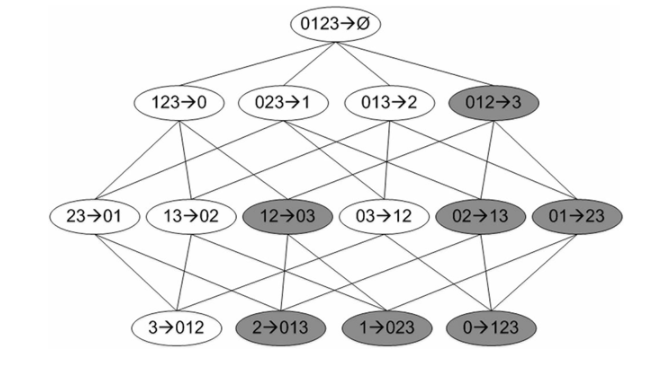
假设图中深色的关联规则为不符合要求的,那么我们在第二轮发现了一个不符合要求的规则,那么我们就可以把它的所有子节点(子孙节点)全部标为深色不用再考虑,意思就是,我们就不用在下一轮考虑这个结点生成的子节点了,这样就省掉了好多计算量。
这样一来,就得到了所有满足阈值的关联规则了~
(这里的话,阈值是一个人为设定的门限值,也就是我们只保留confidence大于这个门限值的关联规则)
我们可能会问,那频繁项集和关联规则有什么用呢?
可以举一个金融的例子:
比如在变化无常的股市中,如果一个行业的突然兴起,我们可以看到这个行业大部分相关的股票都会随之上涨。比如最近很火的区块链概念,有关股票在短时间内都相继上涨;如果我们能够通过挖掘关联规则,发现了一些股票经常同时上涨或者同时下跌,那么这对我们的分析决策将会大大帮助。
| 交易区间 | 股票变动 |
|---|---|
| 0~60 min | 股票a, 股票b, 股票c, 股票d |
| 60~120 min | 股票a, 股票b, 股票c, 股票d |
| 120~180 min | 股票a, 股票b, 股票c, 股票d, |
| 180~240 min | 股票a, 股票b, 股票c, 股票d, |
例如,金融高频数据包含了证券交易过程中更多的实时信息,能够更加准确地捕捉到证券市场发生的每一个细小的变化过程,所以利用高频数据研究股票价格比采用低频数据具有很多的优势。 如果将 Apriori 算法应用到实际的金融高频数据中,可以采用证券市场上几支具有代表性的股票数据,其频率包括五分钟、十五分钟、三十分钟、六十分钟和每日等。通过发现频繁项集,最终生成这几支股票之间的关联规则。它可以更清楚地挖掘出几支股票同涨同跌的相似性。
简单来说呢,就如上表中的4支股票,红色代表上涨,绿色代表下跌;
不难发现,在4个交易区间中,股票a 和 股票c 有三个交易区间都表现为同涨同跌。
所以对于同涨同跌这个问题: {股票a,股票c} 的支持度为 0.75;
{股票a,股票c} 对于 股票a 的可信度也为\(\frac{support(\{股票a,股票c\})}{support(\{股票a\})}=\frac{3/4}{4/4}=\frac{3}{4}\)
那么如果我们看到一顿区间内 股票a 的变动,就有0.75的把握断定 股票c 与股票a 同涨同跌~
总结来说,关联规则就是通过统计规律,发现数据之间的内在联系;
关联规则分析在零售、快消、电商、金融、搜索引擎、智能推荐等领域大有所为,如超市捆绑营销、银行客户交叉销售分析、搜索词推荐或者识别异常、基于兴趣的实时新闻推荐等。
如果能够挖掘到可信度较高的关联规则,加以利用,就能够产生很大的价值。
参考文献:
- https://baike.baidu.com/item/%E5%85%B3%E8%81%94%E8%A7%84%E5%88%99
- 《机器学习实战》人民邮电出版社, Peter Harrington
- 股市K线组合的关联规则挖掘,成都大学学报 第28卷 第三期,王伟钧等