数据结构c++语言描述——最大堆(MaxHeap)
Posted ql698214
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构c++语言描述——最大堆(MaxHeap)相关的知识,希望对你有一定的参考价值。
一、最大堆的插入
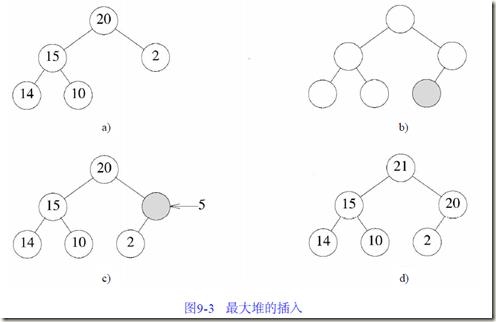
图9-3a 给出了一个具有5个元素的最大堆。由于堆是完全二叉树,当加入一个元素形成6元素堆时,其结构必如9-3b 所示。如果插入元素的值为1,则插入后该元素成为2的左孩子,相反,若新元素的值为5,则该元素不能成为2的左孩子(否则将改变最大树的特性),应把2下移为左孩子(如图9 - 3 c所示),同时还得决定在最大堆中5是否占据2原来的位置。由于父元素20大于等于新插入的元素5,因此可以在原2所在位置插入新的元素。假设新元素的值为21而不是5,这时,同图9-3c 一样,把2下移为左孩子,由于21比父元素值大,所以2 1不能插入原来2所在位置,因此把20移到它的右孩子所在位置, 21插入堆的根节点(如图9-3d所示)。
二、最大堆的删除
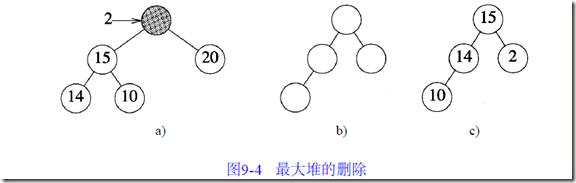
从最大堆中删除一个元素时,该元素从堆的根部移出。例如,对图9-3d的最大堆进行删除操作即是移去元素21,因此最大堆只剩下五个元素。此时,图9-3d中的二叉树需要重新构造,以便仍然为完全二叉树。为此可以移动位置6中的元素,即2。这样就得到了正确的结构(如图9-4a所示),但此时根节点为空且元素2不在堆中,如果2直接插入根节点,得到的二叉树不是最大树,根节点的元素应为2、根的左孩子、根的右孩子三者中的最大值。这个值是20,它被移到根节点,因此在位置3形成一个空位,由于这个位置没有孩子节点,2可以插入,最后形成的最大堆如图9-3a 所示。现在假设要删除20,在删除之后,堆的二叉树结构如图9-4b 所示,为得到这个结构,10从位置5移出,如果将10放在根节点,结果并不是最大堆。把根节点的两个孩子(15和2)中较大的一个移到根节点。假设将10插入位置2,结果仍不是最大堆。因此将14上移,10插入到位置4,最后结果如图9-4c 所示。
三、最大堆的初始化
使用数组初始化一个最大堆,先将数组的元素复制到最大堆中,然后对其进行重新排序,并初始化为最大堆
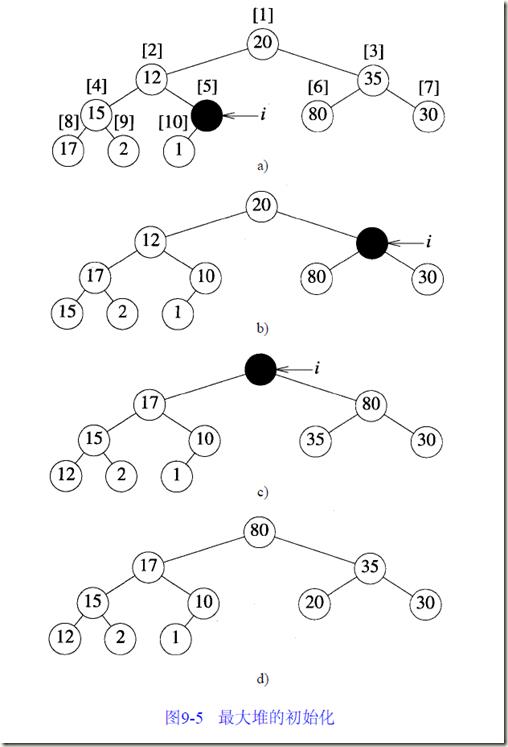
假设开始数组a 中有n 个元素,另有n= 10,a [ 1 : 1 0 ]中元素的关键值为[ 20,12,35,15,10,80,30,17,2,1 ],这个数组可以用来表示如图9-5a 所示的完全二叉树,这棵完全二叉树不是最大树。为了将图9-5a 的完全二叉树转化为最大堆,从第一个具有孩子的节点开始(即节点10),这个元素在数组中的位置为i = [n /2 ],如果以这个元素为根的子树已是最大堆,则此时不需调整,否则必须调整子树使之成为堆。随后,继续检查以i-1, i-2等节点为根的子树,直到检查到整个二叉树的根节点(其位置为1)。下面对图9-5 a中的二叉树完成这一系列工作。最初, i = 5,由于10 > 1,所以以位置i为根的子树已是最大堆。下一步,检查根节点在位置4的子树,由于15 < 17,因此它不是最大堆,为将其变为最大堆,可将15与17进行交换,得到的树如图9-5b 所示。然后检查以位置3为根的子树,为使其变为最大堆,将80与35进行交换。之后,检查根位于位置2的子树,通过重建过程使该子树成为最大堆。将该子树重构为最大堆时需确定孩子中较大的一个,因为12 < 17,所以17成为重构子树的根,下一步将12与位置4的两个孩子中较大的一个进行比较,由于12 < 15,15被移到位置4,空位8没有孩子,将12插入位置8,形成的二叉树如图9-5 c。最后,检查位置1,这时以位置2或位置3为根的子树已是最大堆了,然而20 < (m a x [ 17 , 80 ] ),因此80成为最大堆的根,当80移入根,位置3空出。由于20 <(m a x [ 35 , 30 ] ),位置3被35占据,最后20占据位置6。图9-5d 显示了最终形成的最大堆。
四、源码
1.MaxHeap.h
#pragma once
#include"MyException.h"
/*最大堆*/
template<class T>
class MaxHeap {
public:
MaxHeap(int maxSize=10);
~MaxHeap();
int Size()const;
T Max()const;
MaxHeap<T>& Insert(const T &x);
MaxHeap<T>& DeleteMax(T &x);
void Initialize(T* a, int size, int arraySize);
void Output(ostream& out)const;
private:
int curSize;
int maxSize;
T *heap;
};
template<class T>
MaxHeap<T>::MaxHeap(int maxSize) {
this->maxSize = maxSize;
heap = new T[this->maxSize+1];
curSize = 0;
}
template<class T>
MaxHeap<T>::~MaxHeap() {
delete[] heap;
}
template<class T>
int MaxHeap<T>::Size()const {
return curSize;
}
template<class T>
T MaxHeap<T>::Max()const {
if (curSize == 0)
throw OutOfBounds();
return heap[1];
}
template<class T>
MaxHeap<T>& MaxHeap<T>::Insert(const T &x) {
if (curSize == maxSize) //最大堆满
throw NoMem();
int i = ++curSize; //先增加尺寸,然后i就是要插入位置的坐标
while (i != 1 && x > heap[i / 2]) { //将待插入元素与其父节点进行比较,若大于父节点,则父节点下移,待插入位置移动到父节点
heap[i] = heap[i / 2]; //父节点下移
i = i / 2; //待插入位置移动到父节点
}
heap[i] = x; //最终要插入的位置
return *this;
}
template<class T>
MaxHeap<T>& MaxHeap<T>::DeleteMax(T &x) {
if (curSize == 0)
throw OutOfBounds();
x = heap[1];
//重构堆,并且y保存的是最后一个元素
T y = heap[curSize--];
int i = 1; //堆的当前节点
int ci = 2; //i的孩子
while (ci <= curSize) {
//使得ci为孩子节点中的最大值得坐标
if (ci < curSize && heap[ci] < heap[ci + 1]) {
ci++;
}
if (y >= heap[ci])
break;
//将子节点中的最大值移动到父节点
heap[i] = heap[ci];
i = ci; //父节点下移一层
ci = ci * 2; //子节点下移一层
}
heap[i] = y;
return *this;
}
/*初始化一个非空最大堆
a:输入的一个数组,用于初始化最大堆
size:数组中有效元素的个数(使用a[0]-a[size-1]初始化最大堆)
arraySize:数组的大小*/
template<class T>
void MaxHeap<T>::Initialize(T* a, int size, int arraySize) {
delete[] heap;
curSize = size;
maxSize = arraySize;
heap = new T[maxSize + 1];
for (int i = 1; i <= curSize; i++)
heap[i] = a[i - 1];
for (int i = curSize / 2; i > 0; i--) {
T parent = heap[i];
int childrenIndex = 2 * i;
while (childrenIndex <= curSize) {
//将children移到最大的孩子
if (childrenIndex < curSize && heap[childrenIndex] < heap[childrenIndex + 1]) {
childrenIndex++;
}
//父节点大,不用移动位置
if (parent > heap[childrenIndex])
break;
//父节点小,需要移动位置(此时其子树可能不满足最大堆的性质,因此要下移,通过while循环来使下移的节点成为新的父节点,直到其所有子树均满足最大堆的性质)
heap[childrenIndex / 2] = heap[childrenIndex];
childrenIndex = childrenIndex * 2;//下移一层
}
heap[childrenIndex / 2] = parent;
}
}
template<class T>
void MaxHeap<T>::Output(ostream& out)const {
for (int i = 1; i <= curSize; i++) {
out << heap[i] << " ";
}
}
template<class T>
ostream& operator<<(ostream& out,const MaxHeap<T>& maxHeap) {
maxHeap.Output(out);
return out;
}
2.MyException.h
#include<iostream> #include <string> using namespace std; class NoMem { public: NoMem() { this->message = "内存不足"; } NoMem(string msg) { this->message = msg; } void OutputMessage() { cout << message << endl; } private: string message; }; class OutOfBounds { public: OutOfBounds() { this->message = "输入超过了数组的界"; } OutOfBounds(string msg) { this->message = msg; } void OutputMessage() { cout << message << endl; } private: string message; }; class BadInput { public: BadInput() { this->message = "输入有误"; } BadInput(string msg) { this->message = msg; } void OutputMessage() { cout << message << endl; } private: string message; };
3.主函数
#include"MaxHeap.h"
#include"MyException.h"
#include<iostream>
using namespace std;
void main() {
try {
MaxHeap<int> heap;
int a[10] = { 4,5,2,1,7,3,9,0,6,8 };
heap.Initialize(a, 10, 10);
cout << heap << endl;
cout << "max:" << heap.Max() << endl;
int x = 0;
heap.DeleteMax(x);
cout << heap << endl;
heap.DeleteMax(x);
cout << heap << endl;
heap.DeleteMax(x);
cout << heap << endl;
heap.DeleteMax(x);
cout << heap << endl;
heap.DeleteMax(x);
cout << heap << endl;
cout << "size:" << heap.Size() << endl;
cout << "max:" << heap.Max() << endl;
heap.DeleteMax(x);
cout << heap << endl;
heap.DeleteMax(x);
cout << heap << endl;
heap.DeleteMax(x);
cout << heap << endl;
heap.DeleteMax(x);
cout << heap << endl;
cout << "size:" << heap.Size() << endl;
heap.DeleteMax(x);
cout << heap << endl;
cout << "size:" << heap.Size() << endl;
//heap.DeleteMax(x);
//cout << heap << endl;
//cout << "size:" << heap.Size() << endl;
heap.Insert(4).Insert(3);
cout << heap << endl;
cout << "size:" << heap.Size() << endl;
heap.Insert(6).Insert(100);
cout << heap << endl;
cout << "size:" << heap.Size() << endl;
heap.Insert(40);
cout << heap << endl;
}catch(OutOfBounds o){
o.OutputMessage();
}
system("pause");
}
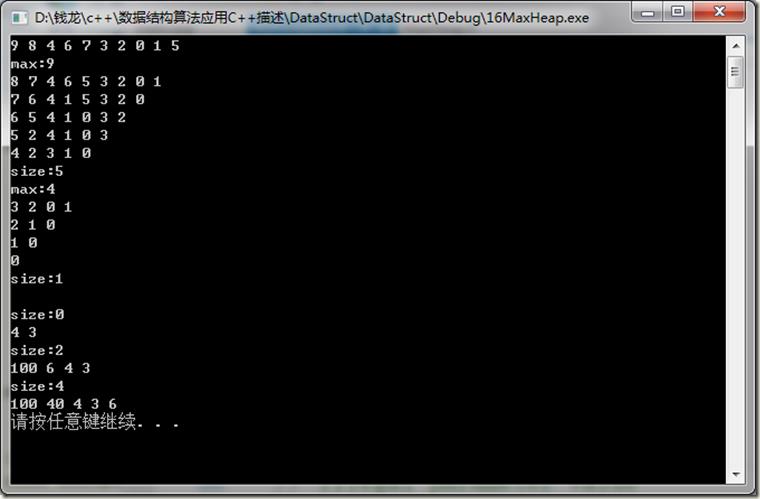
五、程序运行结果
以上是关于数据结构c++语言描述——最大堆(MaxHeap)的主要内容,如果未能解决你的问题,请参考以下文章