贪心算法-图的最短路径算法Dijkstra之证明

Posted 2020-10-26 ordi

一、问题：图的最短路径

　　定义图G=(V,E),而且每条边上的权值非负，求顶点s 到图中任意一点的最短距离。图中任意两点之间的距离定义为：路径上所有边的权值的和。

二、算法：Dijkstra算法

 　　设S是探查的顶点的集合，对每个,我们存储一个距离d(u)

 　　初始S={s},d(s)=0

　　　　While S != V

　　　　　　选择一个顶点使得从S到v至少有一条边并且

　　　　　　

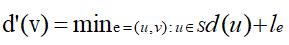
　　　　　　把v加入到S并且定义

　　　　End

三、证明算法的正确性：

　　只需证明，在算法执行中任意一点的集合S，对每个，路径是最短的s-u路径。

 　用数学归纳法证明算法的正确性：

1. |S|=1 时， S={s},d(s)=0 显然成立
2. 假设|S|=k时，命题成立

　　 既对每个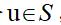，路径P_u是最短的s-u路径

　 3. |S|=k+1

　　 假设此时引入的顶点是v，令(u,v)是s-v路径上最后的一条边。

　　 现在我们证明是s-v的所有路径中最短的路径。

　　 s要到达v，必须首先离开S，然后到达y,最后y到达v

　　 该距离: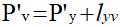

　　 而从Dijkstra算法知，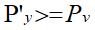

　　 又因为，图中所有边的权值非负，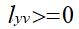

　　 所以有：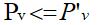

　　    故而P_v是s-v的所有路径中最短的路径。