1、算法概念
2、复习:递归
3、时间复杂度
4、空间复杂度
5、列表查找(顺序查找、二分查找)
6、列表排序
但:请读者了解,无论哪种算法来排序,都没有python自带的函数sort()排序快,因为其底层是c语言写的。
1、算法概念
算法(Algorithm):一个计算过程,解决问题的方法

2、复习:递归
递归的两个特点: 调用自身 结束条件
3、时间复杂度
时间复杂度是用来估计算法运行时间的一个式子(单位)。一般来说,时间复杂度高的算法比复杂度低的算法快。
常见的时间复杂度(按效率排序) O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n3)
不常见的时间复杂度(看看就好) O(n!) O(2n) O(nn) …
如何一眼判断时间复杂度? 循环减半的过程O(logn) 几次循环就是n的几次方的复杂度
1 while n > 1: 2 print(n) 3 n = n // 2 4 5 n=64输出: 6 7 64 8 32 9 16 10 8 11 4 12 2
2^6=64
log264=6
O(log2n) 或 O(logn) 此处2为角标,表示,以2为底n的对数
4、空间复杂度
空间复杂度:用来评估算法内存占用大小的一个式子 “空间换时间”
5、列表查找
列表查找:从列表中查找指定元素
输入:列表、待查找元素
输出:元素下标或未查找到元素
顺序查找 :从列表第一个元素开始,顺序进行搜索,直到找到为止。
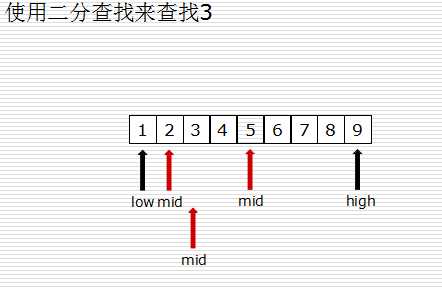
二分查找 :从有序列表的候选区data[0:n]开始,通过对待查找的值与候选区中间值的比较,可以使候选区减少一半。
import time
import random
def cal_time(func): #计时
def wrapper(*args, **kwargs):
t1 = time.time()
result = func(*args, **kwargs)
t2 = time.time()
print("%s running time: %s secs." % (func.__name__, t2 - t1))
return result
return wrapper
#对有序列表进行二分查找
@cal_time
def bin_search(data_set, val):
low = 0
high = len(data_set) - 1
while low <= high:
mid = (low+high)//2
if data_set[mid][‘id‘] == val:
return mid
elif data_set[mid][‘id‘] < val:
low = mid + 1
else:
high = mid - 1
return
‘‘‘
#不要直接放在递归上面
def binary_search(dataset, find_num):
if len(dataset) > 1:
mid = int(len(dataset) / 2)
if dataset[mid] == find_num:
#print("Find it")
return dataset[mid]
elif dataset[mid] > find_num:
return binary_search(dataset[0:mid], find_num)
else:
return binary_search(dataset[mid + 1:], find_num)
else:
if dataset[0] == find_num:
#print("Find it")
return dataset[0]
else:
pass
#print("Cannot find it.")
#不要直接放在递归上面,实在要放应该这样
@cal_time
def binary_search_alex(data_set, val):
return binary_search(data_set, val)
‘‘‘
def random_list(n):
result = []
ids = list(range(1001,1001+n))
a1 = [‘zhao‘,‘qian‘,‘sun‘,‘li‘]
a2 = [‘li‘,‘hao‘,‘‘,‘‘]
a3 = [‘qiang‘,‘guo‘]
for i in range(n):
age = random.randint(18,60)
id = ids[i]
name = random.choice(a1)+random.choice(a2)+random.choice(a3)
data = list(range(100000000))
print(bin_search(data, 173320))
print(binary_search_alex(data, 173320))
6、列表排序
列表排序 :将无序列表变为有序列表
应用场景: 各种榜单 、各种表格、 给二分排序用 、给其他算法用
输入:无序列表
输出:有序列表
排序:
排序low B三人组:冒泡排序 、选择排序 、插入排序
快速排序
排序NB二人组: 堆排序 、归并排序
没什么人用的排序: 基数排序、 希尔排序、 桶排序
冒泡排序:
def bubble_sort(li): for i in range(len(li) - 1): for j in range(len(li) - i - 1): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j] 时间复杂度:O(n^2)
冒泡优化,如果冒泡排序中执行一趟而没有交换,则列表已经是有序状态,可以直接结束算法。优化后的冒泡排序:
def bubble_sort_1(li):
for i in range(len(li) - 1):
exchange = False
for j in range(len(li) - i - 1):
if li[j] > li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
exchange = True
if not exchange:#如果这一趟都没有数字交换,则说明剩下的数字都已经排序好了,直接退出。
break
选择排序 :
一趟遍历记录最小的数,放到第一个位置; 再一趟遍历记录剩余列表中最小的数,继续放置; ……
def select_sort(li):
for i in range(len(li) - 1):
min_loc = i
for j in range(i+1,len(li)):
if li[j] < li[min_loc]:
min_loc = j
li[i], li[min_loc] = li[min_loc], li[i]
插入排序:
列表被分为有序区和无序区两个部分。最初有序区只有一个元素。 每次从无序区选择一个元素,插入到有序区的位置,直到无序区变空。
def insert_sort(li):
for i in range(1, len(li)):
tmp = li[i]
j = i - 1
while j >= 0 and li[j] > tmp:
li[j+1]=li[j]
j = j - 1
li[j + 1] = tmp