公共lcaTarjan

Posted 2020-10-25 dgklr

首先，我们先来了解LCA。

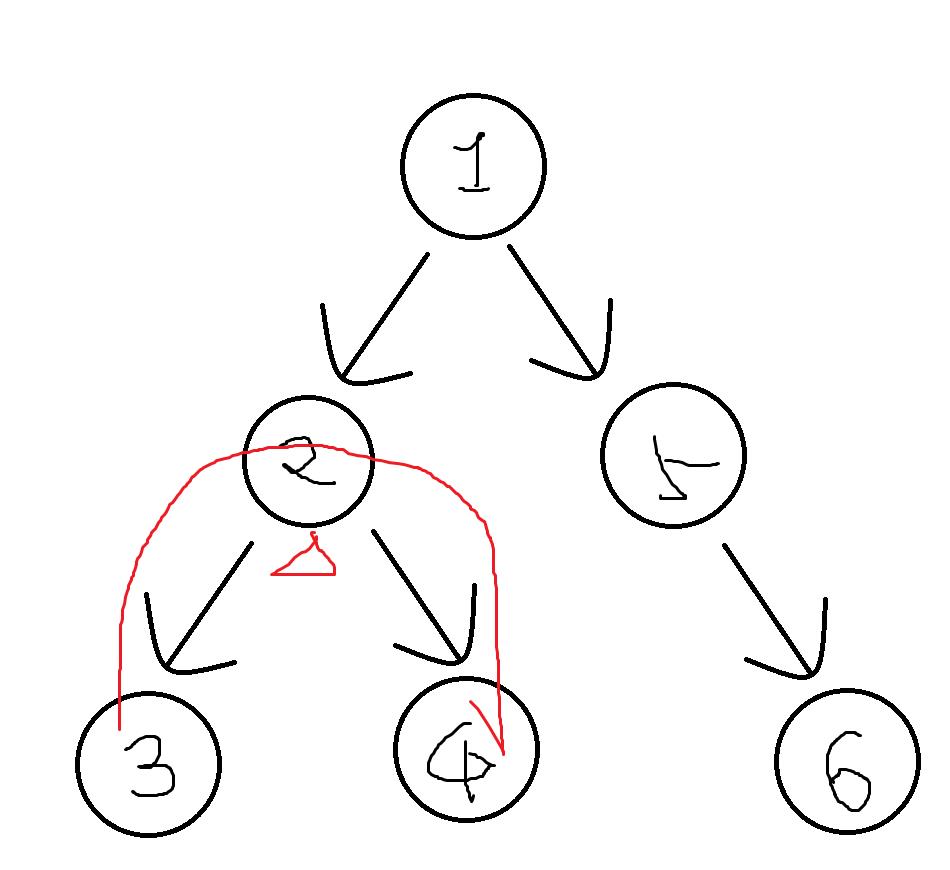
LCA 是树上两个点最近的公共祖先。

比如说，在如图的树中，3与4的公共祖先有“2”，“1”，但最近的祖先是“2”。

显然，暴力可以做O(n)，但是我们希望更快。

现在，有两种方法：

　　1）在线操作，但这需要“倍增”，再此不讨论。

　　2）离线操作，使用Tarjan与并查集。

先给出操作方法：

DFS (u)
   for i in u.son
      DFS(i)
      UNION(u,i)
   for i in u.e # e 表示 e 与访问所有和u有询问关系的i
      if i.vis
         (u,i).LCA = find(i)

可以发现，操作是在深搜中进行的。下面开始模拟。

初始值：

f[1]=1; vis[1]=0;
f[2]=2; vis[2]=0;
f[3]=3; vis[3]=0;
f[4]=4; vis[4]=0;
f[5]=5; vis[5]=0;
f[6]=6; vis[6]=0;

 

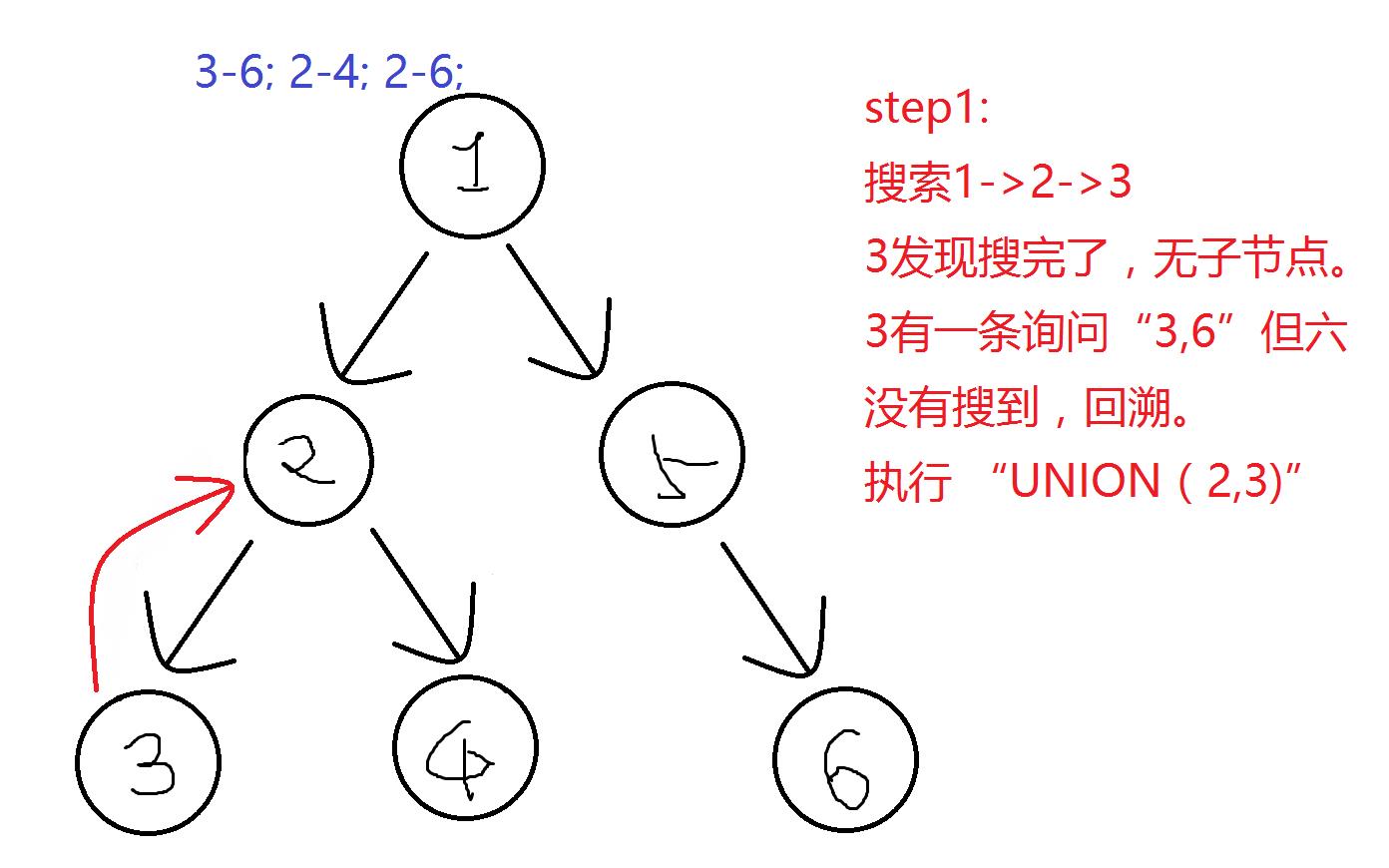
第一次操作后：

f[1]=1; vis[1]=0;
f[2]=2; vis[2]=0;
f[3]=2; vis[3]=1;
f[4]=4; vis[4]=0;
f[5]=5; vis[5]=0;
f[6]=6; vis[6]=0;

 

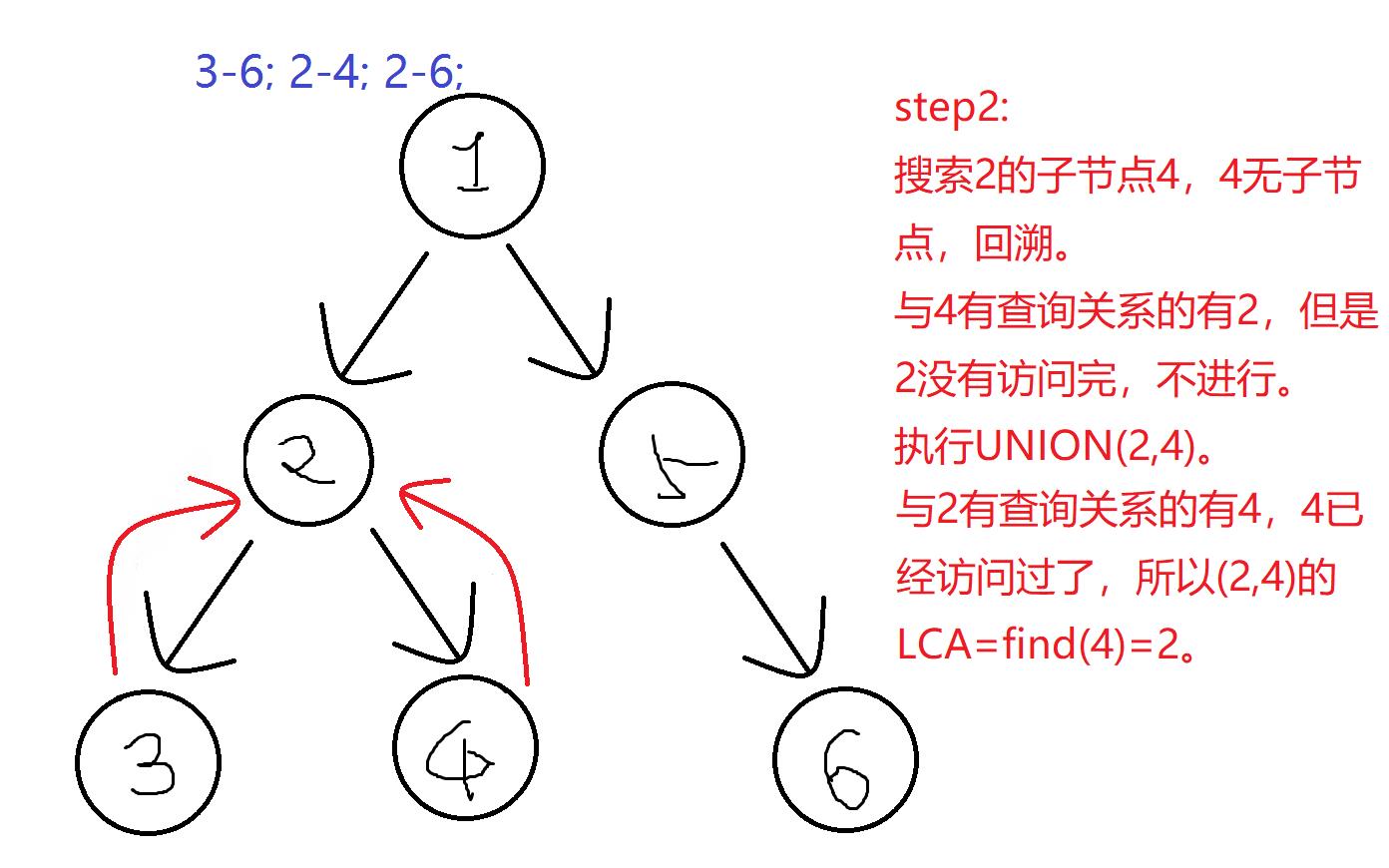
第二次操作后：

f[1]=1; vis[1]=0;
f[2]=2; vis[2]=1;
f[3]=2; vis[3]=1;
f[4]=2; vis[4]=1; 
f[5]=5; vis[5]=0;
f[6]=6; vis[6]=0;

 

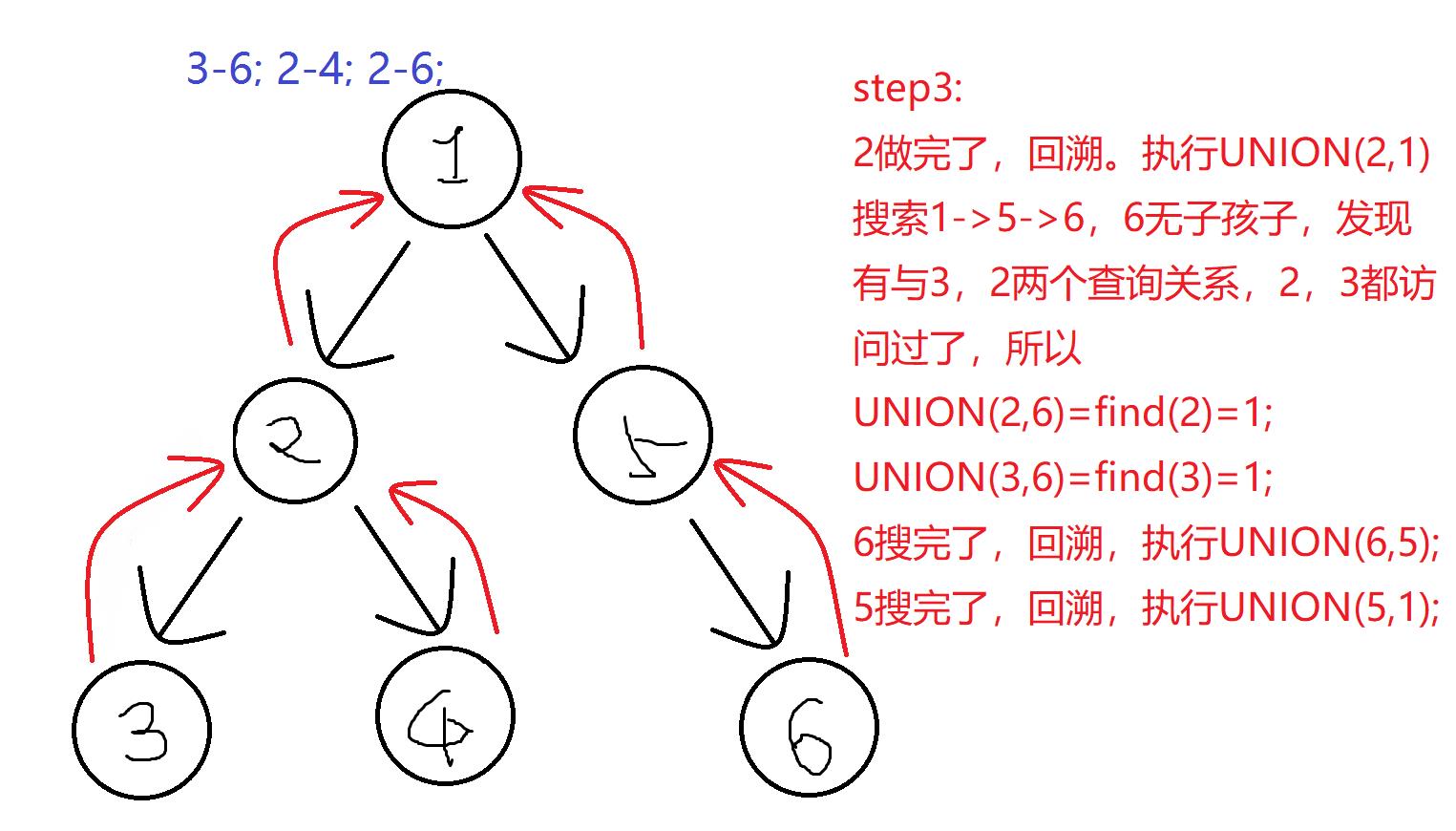
 第三次操作后：

f[1]=1; vis[1]=1;
f[2]=2; vis[2]=1;
f[3]=2; vis[3]=1;
f[4]=2; vis[4]=1;
f[5]=1; vis[5]=1;
f[6]=5; vis[6]=1;

 另附代码：

#include <iostream>  
#include <stdio.h>  
#include <algorithm>  
#include <string.h>  
using namespace std;  
  
const int maxn=10010;
const int maxq=100;   
int f[maxn];
int find(int x)  
{  
    if(f[x]==-1)  
        return x;  
    return f[x]=find(f[x]);  
}  
void unite(int u,int v)  
{  
    int x=find(u);  
    int y=find(v);  
    if(x!=y)  
        f[x]=y;  
}  
  
bool vis[maxn];
int ancestor[maxn];
struct Edge  
{  
    int to,next;  
}edge[maxn*2];  
int head[maxn],tot;  
void addedge(int u,int v)
{  
    edge[tot].to=v;  
    edge[tot].next=head[u];  
    head[u]=tot++;  
}  
  
struct Query  
{  
    int q,next;  
    int index; 
}query[maxq*2];  
int ans[maxn*2];
int h[maxn],tt;  
int Q;
  
void addquery(int u,int v,int index)
{  
    query[tt].q=v;  
    query[tt].next=h[u];  
    query[tt].index=index;  
    h[u]=tt++;  
    query[tt].q=u;
    query[tt].next=h[v];  
    query[tt].index=index;  
    h[v]=tt++;  
}  
  
void init()  
{  
    tot=0;  
    memset(head,-1,sizeof(head));  
    tt=0;  
    memset(h,以上是关于公共lcaTarjan的主要内容，如果未能解决你的问题，请参考以下文章

tarjan,树剖,倍增求lca

有关公共部门人力资源管理论文

最长公共子串和最长公共子序列

公共静态方法与公共方法

MATLAB 最长公共子序列

最长公共子序列与最长公共字串