贪心法_1 2016.5.16

Posted 2020-07-07 __AiR_H

所谓“贪心算法”是指：

在对问题求解时，总是作出在当前看来是最好的选择

也就是说，不从整体上加以考虑，它所作出的仅仅是在某种意义上的局部最优解（是否是全局最优，需要证明）

特别说明：

若要用贪心算法求解某问题的整体最优解，必须首先证明贪心思想在该问题的应用结果就是最优解！！

贪心算法不是对所有问题都能得到整体最优解

关键是贪心策略的选择，选择的贪心策略必须具备无后效性

即某个状态以前的过程不会影响以后的状态，只与当前状态有关

贪心算法的证明

贪心算法的正确性，必须有严格意义的证明，一般使用是归纳法，或者是反证法

但是在程序设计比赛中，只要程序正确运行就好了，严格意思上的算法证明并不是必须的
因此可以说，有足够的自信的话，是不需要证明的
但是有时候不是很确定，在头脑中简单证明一下还是好的

51Nod贪心入门教程_完美字符串

约翰认为字符串的完美度等于它里面所有字母的完美度之和

每个字母的完美度可以由你来分配，不同字母的完美度不同，分别对应一个1-26之间的整数

约翰不在乎字母大小写。（也就是说字母F和f）的完美度相同

给定一个字符串，输出它的最大可能的完美度

例如：dad，你可以将26分配给d，25分配给a，这样整个字符串完美度为77

分析： 由排序不等式，出现次数最多的字母显然应该给26

所以这个题目变成了统计每种字母出现的次数了，然后按照出现次数从大到小，依次分配从高到低的权值

这就是最朴素的贪心思想

输入
输入一个字符串S(S的长度 <= 10000)，S中没有除字母外的其他字符。

输出
由你将1-26分配给不同的字母，使得字符串S的完美度最大，输出这个完美度。

输入示例
dad

输出示例
77

//很久以前写的这个代码，当初还不知道有那些好用的库函数

#include <iostream>
#include <cstdio>
using namespace std;

typedef struct _scord {
    char s;
    int n;
}_Scord;

void Sort(int a[],int n)
{
    int i,j,t;
    for (i=0; i<n-1; i++) {
        for (j=i+1; j<n; j++) {
            if (a[i] < a[j]) {
                t = a[i];
                a[i] = a[j];
                a[j] = t;
            }
        }
    }
}

int main()
{
    char S[10000];
    _Scord scord[26];
    int num[26];
    int i,j;
    int sum = 0;
    int s_num = 0;
    int flag = 0;
    while (cin>>S) {
        scord[0].s = S[0];
        scord[0].n = 1;
        for (i=1,s_num=0; S[i]!='\\0'; i++) {
            for (j=0,flag=0; j<s_num+1; j++) {
                if (S[i]==scord[j].s || S[i]==scord[j].s-32 || S[i]==scord[j].s+32) {
                    scord[j].n++;
                    flag = 1;
                    break;
                }
            }
            if (0 == flag) {
                s_num++;
                scord[s_num].s = S[i];
                scord[s_num].n = 1;
            }
        }
        for (i=0; i<s_num+1; i++) {
            num[i] = scord[i].n;
        }
        Sort(num,(s_num+1));
        for (i=0,sum=0; i<s_num+1; i++) {
            sum += num[i] * (26 - i);
        }
        cout<<sum<<endl;
    }

    return 0;
}

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;

const int INF = 0x7fffffff;
const int maxn = 1e4 + 10;
char S[maxn];
int vis[30];

int cmp_num(const void* a, const void* b);

int main()
{
#ifdef __AiR_H
    freopen("in.txt", "r", stdin);
#endif // __AiR_H
    gets(S);
    strlwr(S);
    int len = strlen(S);
    memset(vis, 0, sizeof(vis));
    for (int i = 0; i < len; ++i) {
        int t = S[i] - 'a';
        ++vis[t];
    }
    qsort(vis, 26, sizeof(vis[0]), cmp_num);
    int ans = 0;
    for (int i = 0, j = 26; i < 26 && vis[i] != 0; ++i, --j) {
        ans += vis[i] * j;
    }
    printf("%d\\n", ans);
    return 0;
}

int cmp_num(const void* a, const void* b)
{
    return (*(int*)b - *(int*)a) > 0 ? 1 : -1;
}

51Nod贪心入门教程_独木舟问题

n个人，已知每个人体重，独木舟承重固定，每只独木舟最多坐两个人，可以坐一个人或者两个人

显然要求总重量不超过独木舟承重，假设每个人体重也不超过独木舟承重，问最少需要几只独木舟？

分析：

一个显然的策略是按照人的体重排序

极端化贪心策略，最重的人要上船——如果最重的人和最轻的人体重总和不超过船的承重，则他们两个占用一条船

否则（因为假设最重的人的体重也不超过船的承重了），最重的人单独占一条船

转变为(n – 1)或者(n – 2)的问题了

关键在于这种贪心策略是正确的

我们可以证明，最优解也可以变为这种策略

（1） 假设最重的人和最轻的人的体重和超过了船的承重，那么最优解中，显然也是最重的人单独占一条船，所以这种情况下最优解和贪心策略是相同的
（2） 假设最重的人和最轻的人的体重和没超过船的承重

（2.1）如果最优解中，最重的人单独占用一条船，则可以把最轻的人也放上去，这样最优解用的船数不增加

如果最轻的人占用一条船，同样我们可以把最重的人放上去，最优解船数不增

（2.2） 如果最优解中最重的人x和x’占用一只船(x, x’)，而最轻的人y和y’占用一只船(y, y’)
我们换成(x, y) (x’,y’)

(x, y)显然没超过船的承重——因为我们假设就是如此。关键看(x’, y’)

x’ + y’<= x’ + x 因为(x’, x)没超重，所以(x’,y’)也合法。所以换一下，最优解船数也不增

这样我们就证明了如果可能把最重的人和最轻的人放在一条船上，不会影响最优解

反复应用这个策略，就可以把n降低为(n – 1)或者(n – 2)个人的规模，从而解决这个问题

输入
第一行包含两个正整数n (0<n<=10000)和m (0<m<=2000000000)，表示人数和独木舟的承重
接下来n行，每行一个正整数，表示每个人的体重。体重不超过1000000000，并且每个人的体重不超过m

输出
一行一个整数表示最少需要的独木舟数。

输入示例
3 6
1
2
3

输出示例
2

#include <iostream>
using namespace std;

void Sort(int a[],int n)
{
    int i,j,t;
    for (i=0; i<n-1; i++) {
        for (j=i+1; j<n; j++) {
            if (a[i] > a[j]) {
                t = a[i];
                a[i] = a[j];
                a[j] = t;
            }
        }
    }
}

int main()
{
    int n,m;
    int i,j,k;
    int num = 0;
    int weight[10000] = {0};
    int f_num,s_num;
    while (cin>>n>>m) {
        for (i=0; i<n; i++) {
            cin>>weight[i];
        }

        Sort(weight,i);

        f_num = 0;
        s_num = i-1;

        for (j=0,num=0; j<i-1; j++) {

            if (weight[f_num]+weight[s_num] <= m) {
                num++;
                f_num++;
                s_num--;
            } else {
                num++;
                s_num--;
            }
            if (1 == f_num-s_num) {
                break;
            }
            if (f_num == s_num) {
                num++;
                break;
            }
        }

        cout<<num<<endl;
    }
    return 0;
}

51Nod贪心入门教程_活动安排问题

有若干个活动，第i个开始时间和结束时间是[Si,fi)，只有一个教室，活动之间不能交叠，求最多安排多少个活动？

分析： 我们就是想提高教室地利用率，尽可能多地安排活动
考虑容易想到的几种贪心策略：

（1） 开始最早的活动优先，目标是想尽早结束活动，让出教室
然而， 这个显然不行，因为最早的活动可能很长，影响我们进行后面的活动

例如活动开始和结束时间分别为[0, 100), [1,2) ,[2, 3), [3, 4),[4,5]，安排［0，100)的这个活动之后，其他活动无法安排，可是最优解是安排除它外的4个活动

（2） 短活动优先， 目标也是尽量空出教室

但是不难构造如下反例： [0,5) [5,10) [3, 7), 这里[3,7)最短，但如果我们安排了[3,7)，其它两个无法安排了

但是最优解显然是安排其它两个，而放弃[3,7)，可见这个贪心策略也是不行的

（3） 最少冲突的活动优先， 既然上面安排活动是想减少冲突，那么如果我们优先安排冲突最少的活动可以么？

至少从（1）和（2）看来，这个策略是有效的

真是对的么？ 尝试这个例子：

[0,2) [2,4) [4,6) [6,8)
[1,3) [1,3) [1,3) [3,5) [5,7) [5,7) [5,7)

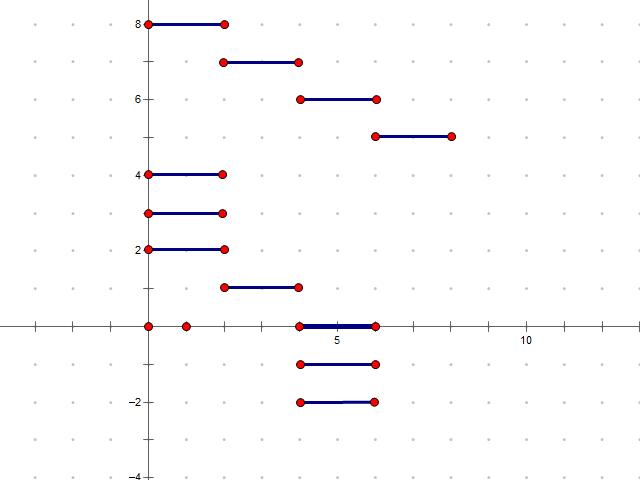
看一下[0,2) 和3个活动冲突——3个[1,3)

[2,4)和4个活动冲突3个[1,3)和一个[3,5)
[4,6)和也和4个活动冲突3个[5,7)和一个[3,5)
[6,8)和3个活动冲突——3个[5,7)

下面[1,3)和[5,7)每个都和5个活动冲突
而[3,5)只和两个活动冲突——[2,4)和[4,6)

那按照我们的策略应该先安排[3,5), 可是一旦选择了[3,5)，我们最多只可能安排3个活动
但明显第一行的4个活动都可以安排下来，所以这种策略也是不对的

（4） 看似最不对的策略——结束时间越早的活动优先

这个策略是有效的，我们可以证明

假设最优解OPT中安排了m个活动，我们把这些活动也按照结束时间由小到大排序，显然是不冲突的

假设排好顺序后，这些活动是a(1) , a(2), a(3)….am

假设按照我们的贪心策略，选出的活动自然是按照结束时间排好顺序的，并且也都是不冲突的，这些活动是b(1), b(2) …b(n)

问题关键是，假设a(1) = b(1), a(2) = b(2)…. a(k) = b(k)，但是a(k+1) != b(k+1)，回答几个问题：

(1)b(k+1)会在a(k+2), a(k+3), …. a(m)中出现么？
不会。

因为b(k+1)的结束时间是最早的，即f(b(k+1)) <= f(a(k+1)),而a(k+2), a(k+3), …. a(m)的开始时间和结束时间都在f(a(k+1))之后，所以b(k+1)不在其中

(2)b(k+1)和a(1), a(2), …. a(k) 冲突么？
不冲突，因为a(1), a(2), …. a(k)就是b(1), b(2), …. b(k)

(3)b(k+1)和a(k+2), a(k+3), …. a(m)冲突么？
不冲突，因为f(b(k+1)) <= f(a(k+1))，而a(k+2), a(k+3), …. a(m)的开始时间都在f(a(k+1))之后，更在f(b(k+1))之后。

因此我们可以把a(k+1) 换成b(k+1)， 从而最优解和我们贪心得到的解多了一个相同的

经过一个一个替换，我们可以把最优解完全替换成我们贪心策略得到的解

从而证明了这个贪心策略的最优性

输入
第1行：1个数N，线段的数量(2 <= N <= 10000)
第2 - N + 1行：每行2个数，线段的起点和终点(-10^9 <= S,E <= 10^9)

输出
输出最多可以选择的线段数量。

输入示例
3
1 5
2 3
3 6

输出示例
2

#include <iostream>
using namespace std;

void Sort(int a[],int b[],int n)
{
    int i,j,t;
    for (i=0; i<n-1; i++) {
        for (j=i+1; j<n; j++) {
            if (a[i] > a[j]) {
                t = a[i];
                a[i] = a[j];
                a[j] = t;
                t = b[i];
                b[i] = b[j];
                b[j] = t;
            }
        }
    }
}

int main()
{
    int n;
    int i,j;
    int left[10000] = {0};
    int right[10000] = {0};
    int right_val = 0;
    int num = 1;
    while (cin>>n) {
        for (i=0; i<n; i++) {
            cin>>left[i]>>right[i];
        }
        Sort(right,left,i);
        for (j=1,num=1,right_val=right[0]; j<i; j++) {
            if (left[j] >= right_val) {
                num++;
                right_val = right[j];
            }
        }
        cout<<num<<endl;
    }
    return 0;
}

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;

const int INF = 0x3f3f3f3f;
const int maxn = 10000 + 10;

struct Node {
    int s, e;
};

Node node[maxn];

int cmp_num(const void* a, const void* b);

int main()
{
#ifdef __AiR_H
    freopen("in.txt", "r", stdin);
#endif // __AiR_H
    int n;
    while (scanf("%d", &n) != EOF) {
        for (int i = 0; i < n; ++i) {
            scanf("%d%d", &node[i].s, &node[i].e);
        }
        qsort(node, n, sizeof(node[0]), cmp_num);
        int Count = 1;
        int now_e = node[0].e;
        for (int i = 1; i < n; ++i) {
            if (node[i].s >= now_e) {
                now_e = node[i].e;
                ++Count;
            }
        }
        printf("%d\\n", Count);
    }
    return 0;
}

int cmp_num(const void* a, const void* b)
{
    Node* x = (Node*)a;
    Node* y = (Node*)b;
    return (x->e - y->e) > 0 ? 1 : -1;
}

HDU 2037 今年暑假不AC

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;

const int INF = 0x3f3f3f3f;
const int maxn = 100 + 10;

struct Node {
    int s, e;
};

Node node[maxn];

int cmp_num(const void* a, const void* b);

int main()
{
#ifdef __AiR_H
    freopen("in.txt", "r", stdin);
#endif // __AiR_H
    int n;
    while (scanf("%d", &n) != EOF && n != 0) {
        for (int i = 0; i < n; ++i) {
            scanf("%d%d", &node[i].s, &node[i].e);
        }
        qsort(node, n, sizeof(node[0]), cmp_num);
        int Count = 1;
        int now_e = node[0].e;
        for (int i = 1; i < n; ++i) {
            if (node[i].s >= now_e) {
                now_e = node[i].e;
                ++Count;
            }
        }
        printf("%d\\n", Count);
    }
    return 0;
}

int cmp_num(const void* a, const void* b)
{
    Node* x = (Node*)a;
    Node* y = (Node*)b;
    return (x->e - y->e) > 0 ? 1 : -1;
}

51Nod贪心入门教程_活动安排问题之二

有若干个活动，第i个开始时间和结束时间是[Si,fi)，活动之间不能交叠，要把活动都安排完，至少需要几个教室？

分析：

能否按照之一问题的解法，每个教室安排尽可能多的活动

即按结束时间排序，再贪心选择不冲突的活动，安排一个教室之后，剩余的活动再分配一个教室，继续贪心选择……

反例： A：[1,2)  B：[1,4) C：[5,6) D：[3，7)

已经按结束时间排好顺序，我们会选择
教室1： A C
教室2:  B
教室3:  D
需要3个教室
但是如果换一种安排方法，我们可以安排AD在一个教室，而BC在另外一个教室，两个教室就够了

所以之前的贪心策略解决不了这个问题
怎么办？

之前的策略是用一个教室找所有它能安排下的活动，即用教室找活动，我们能不能用活动找教室呢？

策略：

按照开始时间排序优先安排活动，如果冲突，则加一个教室
简单地理解一下，策略是这样，我们把活动按照开始时间有小到大的顺序排序

假设目前已经分配了k个教室（显然k初始等于0），对于当前这个活动
（1） 如果它能安排在k个教室里的某一个，则把它安排在其中的任何一个教室里，k不变
（2） 否则它和每个教室里的活动都冲突，则增加一个教室，安排这个活动

这个策略是最优么？

我们想像一下k增加1的过程：

因为我们是按照开始时间排序的，意味着当前考虑的这个活动开始的时候，k个教室里都有活动没结束

（因为如果有一个教室的活动结束了，我们就可以安排这个活动进入那个教室而不冲突，从而不用增加k)

这就意味着在这个活动开始的时间点，算上目前考虑的这个活动，有(k + 1)个活动正在进行，同一时刻有(k + 1)个活动在进行

无论我们如何安排教室，都至少需要(k + 1)个教室

因为每个教室里不能同时进行两个活动。而我们的策略恰好需要(k + 1)个教室，所以是最优的

这个策略也告诉我们，如果从时间轴上“宏观”考虑这个问题

考虑每个时间点同时进行的活动个数，作为这个时间点的厚度

（把活动开始和结束时间想像成线段，那么每个时间点有多少条线段覆盖它，可以简单理解为“厚度”）

我们至少需要最大厚度那么多个教室——因为那时恰好有最大厚度那么多个活动同时进行

而我们这个贪心策略恰好给了我们一个用最大厚度那么多个教室安排全部活动的一个方案

如果只需要教室的个数，我们可以把所有开始时间和结束时间排序，遇到开始时间就把厚度加1，遇到结束时间就把厚度减1

显然最初始和最后结束时的厚度是0，在一系列厚度变化的过程中，峰值（最大值）就是最多同时进行的活动数，也是我们至少需要的教室数

输入
第一行一个正整数n (n <= 10000)代表活动的个数。
第二行到第(n + 1)行包含n个开始时间和结束时间。
开始时间严格小于结束时间，并且时间都是非负整数，小于1000000000

输出
一行包含一个整数表示最少教室的个数。

输入示例
3
1 2
3 4
2 9

输出示例
2

#include <iostream>
using namespace std;

void Sort(int a[],int b[],int n)
{
    int i,j,t;
    for (i=0; i<n-1; i++) {
        for (j=i+1; j<n; j++) {
            if (a[i] > a[j]) {
                t = a[i];
                a[i] = a[j];
                a[j] = t;
                t = b[i];
                b[i] = b[j];
                b[j] = t;
            }
        }
    }
}

int main()
{
    int n;
    int i,j,k;
    int left[10000] = {0};
    int right[10000] = {0};
    int Class[10000] = {0};
    int num = 0;
    int flag = 0;
    while (cin>>n) {
        for (i=0; i<n; i++) {
            cin>>left[i]>>right[i];
        }

        Sort(left,right,i);
        Class[0] = right[0];
        for (j=1,num=0; j<i; j++) {
            for (k=0,flag=0; k<num+1; k++) {
                if (left[j] >= Class[k]) {
                    Class[k] = right[j];
                    flag = 1;
                    break;
                }
            }
            if (0 == flag) {
                num++;
                Class[num] = right[j];
            }
        }
        cout<<num+1<<endl;
    }
    return 0;
}

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;

const int INF = 0x3f3f3f3f;
const int maxn = 10000 + 10;

struct Node {
    int s, e;
};

Node node[maxn];
int Class[maxn];

bool cmp_num(const Node a, const Node b);

int main()
{
#ifdef __AiR_H
    freopen("in.txt", "r", stdin);
#endif // __AiR_H
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        scanf("%d%d", &node[i].s, &node[i].e);
    }
    sort(node, node+n, cmp_num);
    int Count = 0;
    for (int i = 0; i < n; ++i) {
        bool flag = false;
        for (int j = 0; j < Count; ++j) {
            if (node[i].s >= Class[j]) {
                flag = true;
                Class[j] = node[i].e;
                break;
            }
        }
        if (!flag) {
            Class[Count] = node[i].e;
            ++Count;
        }
    }
    printf("%d\\n", Count);
    return 0;
}

bool cmp_num(const Node a, const Node b)
{
    return (a.s < b.s);
}