图片经过卷积、激活后的结果一般带有大量原图信息。
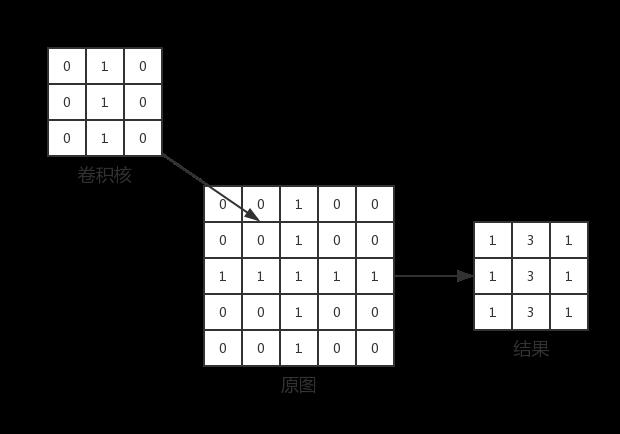
上图中卷积核提取的是竖直方向上的连续像素,但是,被增强的像素只占了结果的1/3,对于多层网络,其余重要性较低的信息也被传入了下一层网络,造成了不必要的浪费,因此需要用池化对卷基层得到的结果做聚合统计。池化的理论基础是:图像相邻位置的像素是相关的,即使间隔一段尺寸对图像进行采样,得到的结果依旧能保持大部分信息。常用的池化方式有最大池化和均值池化。池化的另一个重要作用是为卷积神经网络带来一定的平移、旋转和透视不变性。
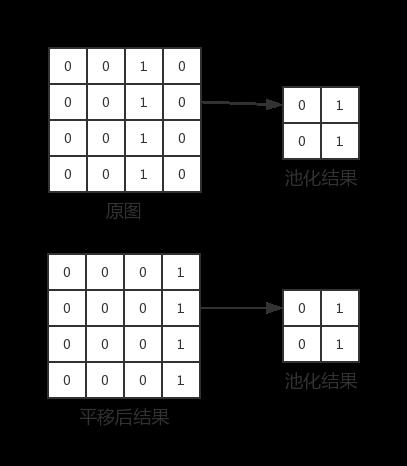
上图展示了池化如何为模型带来平移不变性。原图中垂直方向上的一段连续像素被右移了一个单位得到了平移后的图片,两者经过尺寸为2*2,步长为1的最大池化后,得到了相同的结果。对于旋转和透视,池化也可以达到类似的效果。但池化使模型具有对平移、旋转、透视的抗性并不是没有限制的,首先池化的效果依赖于卷积的结果,如果卷积没有捕捉到上述变换后的特征,池化也失去了抗平移、旋转、透视的能力,其次,池化对上述三种变换的抗性和池化的尺寸有关,池化尺寸越大,抗性越强,但信息丢失的也越多,其中利弊需要设计者权衡。