摘要
本章介绍了几种基本的数据结构,包括栈、队列、链表以及有根树,讨论了使用指针的简单数据结构来表示动态集合。本章的内容对于学过数据结构的人来说,没有什么难处,简单的总结一下。
1、栈和队列
栈和队列都是动态集合,元素的出入是规定好的。栈规定元素是先进后出(FILO),队列规定元素是先进先出(FIFO)。栈和队列的实现可以采用数组和链表进行实现。在标准模块库STL中有具体的应用,可以参考http://www.cplusplus.com/reference/。
栈的基本操作包括入栈push和出栈pop,栈有一个栈顶指针top,指向最新如栈的元素,入栈和出栈操作操作都是从栈顶端进行的。
队列的基本操作包括入队enqueue和出队dequeue,队列有队头head和队尾tail指针。元素总是从队头出,从队尾入。采用数组实现队列时候,为了合理利用空间,可以采用循环实现队列空间的有效利用。
关于栈和队列的基本操作如下图所示: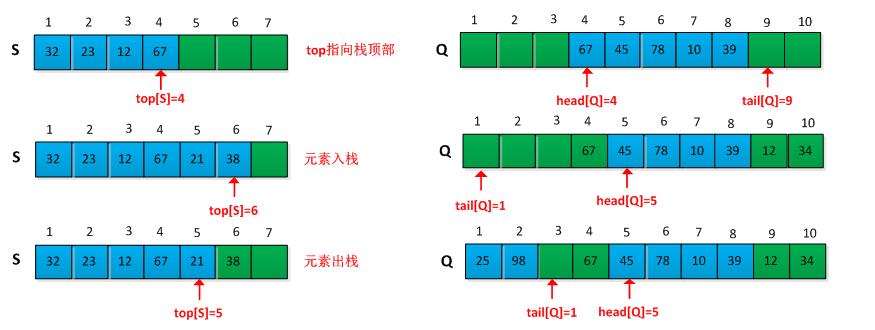
采用数组简单实现一下栈和队列,实现队列时候,长度为n的数组最多可以含有n-1个元素,循环利用,这样方便判断队列是空还是满。程序如下所示:
1 //stack.c
2
3 #include <stdio.h>
4 #include <stdlib.h>
5
6 typedef struct stack
7 {
8 int *s;
9 int stacksize;
10 int top;
11 }stack;
12
13 void init_stack(stack*s)
14 {
15 s->stacksize = 100;
16 s->s =(int*)malloc(sizeof(int)*s->stacksize);
17 s->top = -1;
18 }
19 int stack_empty(stack s)
20 {
21 return ((0 == s.stacksize) ? 1 : 0);
22 }
23
24 void push(stack *s,int x)
25 {
26 if(s->top == s->stacksize)
27 printf("up to overflow.\\n");
28 else
29 {
30 s->top++;
31 s->s[s->top] = x;
32 s->stacksize++;
33 }
34 }
35 void pop(stack *s)
36 {
37 if(0 == s->stacksize)
38 printf("down to overflow.\\n");
39 else
40 {
41 s->top--;
42 s->stacksize--;
43 }
44 }
45 int top(stack s)
46 {
47 return s.s[s.top];
48 }
49
50 int main()
51 {
52 stack s;
53 init_stack(&s);
54 push(&s,19);
55 push(&s,23);
56 push(&s,34);
57 push(&s,76);
58 push(&s,65);
59 printf("top is:%d\\n",top(s));
60 pop(&s);
61 printf("top is:%d\\n",top(s));
62 }
1 #include <stdio.h>
2 #include <stdlib.h>
3
4 typedef struct queue
5 {
6 int *q;
7 int queuesize;
8 int head;
9 int tail;
10 }queue;
11
12 void enqueue(queue* q,int x)
13 {
14 if(((q->tail+1) % q->queuesize) == q->head)
15 {
16 printf("queue is full.\\n");
17 }
18 else
19 {
20 q->q[q->tail] = x;
21 q->tail = (q->tail+1) % q->queuesize;
22 }
23 }
24
25 int dequeue(queue* q,int *value)
26 {
27 if(q->tail == q->head)
28 return -1;
29 else
30 {
31 *value = q->q[q->head];
32 q->head = ((q->head++) % q->queuesize);
33 }
34 }
35 int main()
36 {
37
38 int value;
39 queue q;
40 q.queuesize=10;
41 q.q = (int*)malloc(sizeof(int)*q.queuesize);
42 q.head=0;
43 q.tail=0;
44 enqueue(&q,10);
45 enqueue(&q,30);
46 printf("head=%d\\t tail=%d\\n",q.head,q.tail);
47 if(dequeue(&q,&value) == -1)
48 printf("queue is empty.\\n");
49 else
50 printf("value=%d\\n",value);
51 if(dequeue(&q,&value) == -1)
52 printf("queue is empty.\\n");
53 else
54 printf("value=%d\\n",value);
55 if(dequeue(&q,&value) == -1)
56 printf("queue is empty.\\n");
57 else
58 printf("value=%d\\n",value);
59 printf("head=%d\\t tail=%d\\n",q.head,q.tail);
60 enqueue(&q,10);
61 exit(0);
62 }
测试结果如下所示:

问题:
(1)说明如何用两个栈实现一个队列,并分析有关队列操作的运行时间。
解答:栈中的元素是先进后出,而队列中的元素是先进先出。现有栈s1和s2,s1中存放队列中的结果,s2辅助转换s1为队列。入队列操操作:当一个元素入队列时,先判断s1是否为空,如果为空则新元素直接入s1,如果非空则将s1中所有元素出栈并存放到s2中,然后在将元素入s1中,最后将s2中所有元素出栈并入s1中。此时s1中存放的即是队列入队的顺序。出队操作:如果s1为空,则说明队列为空,非空则s1出栈即可。入队过程需要在s1和s2来回交换,运行时间为O(n),出队操作直接是s1出栈运行时间为O(1)。举例说明转换过程,如下图示:
我采用C++语言实现整程序如下:
1 #include <iostream>
2 #include <stack>
3 #include <cstdlib>
4 using namespace std;
5
6 template <class T>
7 class MyQueue
8 {
9 public:
10 MyQueue();
11 ~MyQueue();
12 void enqueue(const T& data);
13 int queue_empty() const;
14 T dequeue();
15 private:
16 stack<T>s1;
17 stack<T>s2;
18 };
19
20 template<class T>
21 MyQueue<T>::MyQueue()
22 {
23
24 }
25 template<class T>
26 MyQueue<T>::~MyQueue()
27 {
28
29 }
30 template<class T>
31 void MyQueue<T>::enqueue(const T& data)
32 {
33 if(s1.empty())
34 s1.push(data);
35 else
36 {
37 while(!s1.empty(d))
38 {
39 s2.push(s1.top());
40 s1.pop();
41 }
42 s1.push(data);
43 }
44 while(!s2.empty())
45 {
46 s1.push(s2.top());
47 s2.pop();
48 }
49 }
50 template<class T>
51 int MyQueue<T>::queue_empty() const
52 {
53 return (s1.empty());
54 }
55 template<class T>
56 T MyQueue<T>::dequeue()
57 {
58 T ret;
59 if(!s1.empty())
60 {
61 ret = s1.top();
62 s1.pop();
63 }
64 return ret;
65
66 }
67
68 int main()
69 {
70 MyQueue<int> myqueue;
71 myqueue.enqueue(10);
72 myqueue.enqueue(20);
73 myqueue.enqueue(30);
74 cout<< myqueue.dequeue()<<endl;
75 myqueue.enqueue(40);
76 cout<< myqueue.dequeue()<<endl;
77 cout<< myqueue.dequeue()<<endl;
78 myqueue.enqueue(50);
79 cout<< myqueue.dequeue()<<endl;
80 cout<< myqueue.dequeue()<<endl;
81 exit(0);
82 }
(2)说明如何用两个队列实现一个栈,并分析有关栈操作的运行时间。
解答:类似上面的题目,队列是先进先出,而栈是先进后出。现有队列q1和q2,q1中存放的是栈的结果,q2辅助q1转换为栈。入栈操作:当一个元素如栈时,先判断q1是否为空,如果为空则该元素之间入队列q1,如果非空则将q1中的所有元素出队并入到q2中,然后将该元素入q1中,最后将q2中所有元素出队并入q1中。此时q1中存放的就是栈的如栈顺序。出栈操作:如果q1为空,则栈为空,否则直接q1出队操作。入栈操作需要在队列q1和q2直接来来回交换,运行时间为O(n),出栈操作是队列q1出队操作,运行时间为O(1)。我用C++语言实现完整程序如下:
1 #include <iostream>
2 #include <stack>
3 #include <cstdlib>
4 using namespace std;
5
6 template <class T>
7 class MyQueue
8 {
9 public:
10 MyQueue();
11 ~MyQueue();
12 void enqueue(const T& data);
13 int queue_empty() const;
14 T dequeue();
15 private:
16 stack<T>s1;
17 stack<T>s2;
18 };
19
20 template<class T>
21 MyQueue<T>::MyQueue()
22 {
23
24 }
25 template<class T>
26 MyQueue<T>::~MyQueue()
27 {
28
29 }
30 template<class T>
31 void MyQueue<T>::enqueue(const T& data)
32 {
33 if(s1.empty())
34 s1.push(data);
35 else
36 {
37 while(!s1.empty(d))
38 {
39 s2.push(s1.top());
40 s1.pop();
41 }
42 s1.push(data);
43 }
44 while(!s2.empty())
45 {
46 s1.push(s2.top());
47 s2.pop();
48 }
49 }
50 template<class T>
51 int MyQueue<T>::queue_empty() const
52 {
53 return (s1.empty());
54 }
55 template<class T>
56 T MyQueue<T>::dequeue()
57 {
58 T ret;
59 if(!s1.empty())
60 {
61 ret = s1.top();
62 s1.pop();
63 }
64 return ret;
65
66 }
67
68 int main()
69 {
70 MyQueue<int> myqueue;
71 myqueue.enqueue(10);
72 myqueue.enqueue(20);
73 myqueue.enqueue(30);
74 cout<< myqueue.dequeue()<<endl;
75 myqueue.enqueue(40);
76 cout<< myqueue.dequeue()<<endl;
77 cout<< myqueue.dequeue()<<endl;
78 myqueue.enqueue(50);
79 cout<< myqueue.dequeue()<<endl;
80 cout<< myqueue.dequeue()<<endl;
81 exit(0);
82 }
2、链表
链表与数组的区别是链表中的元素顺序是有各对象中的指针决定的,相邻元素之间在物理内存上不一定相邻。采用链表可以灵活地表示动态集合。链表有单链表和双链表及循环链表。书中着重介绍了双链表的概念及操作,双链表L的每一个元素是一个对象,每个对象包含一个关键字和两个指针:next和prev。链表的操作包括插入一个节点、删除一个节点和查找一个节点,重点来说一下双向链表的插入和删除节点操作,图例如下:

链表是最基本的数据结构,凡是学计算机的必须的掌握的,在面试的时候经常被问到,关于链表的实现,百度一下就知道了。在此可以讨论一下与链表相关的练习题。
(1)在单链表上插入一个元素,要求时间复杂度为O(1)。
解答:一般情况在链表中插入一元素是在末尾插入的,这样需要从头遍历一次链表,找到末尾,时间为O(n)。要在O(1)时间插入一个新节点,可以考虑每次在头节点后面插入,即每次插入的节点成为链表的第一个节点。
(2)在单链表上删除一个给定的节点p,要求时间复杂度为O(1)。
解答:一般情况删除一个节点时候,我们需要找到该节点p的前驱节点q,需要对链表进行遍历,运行时间为O(n-1)。我们可以考虑先将q的后继节点s的值替换q节点值,然后删除s即可。如下图删除节点q的操作过程:

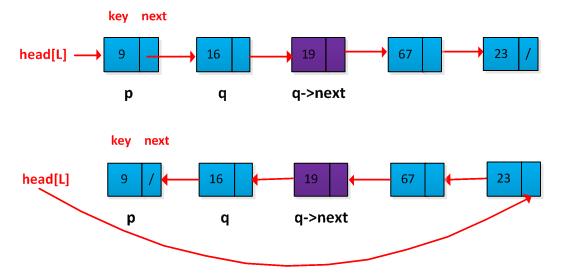
(3)单链表逆置,不允许额外分配存储空间,不允许递归,可以使用临时变量,执行时间为O(n)。
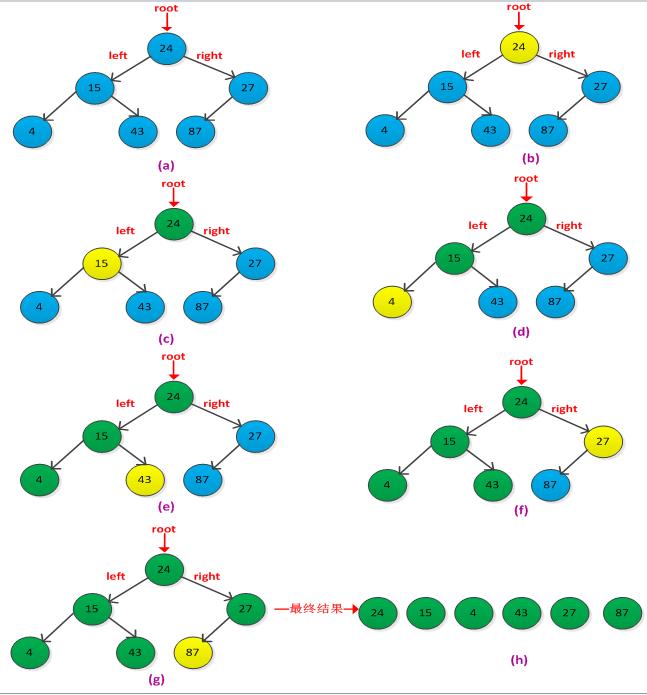
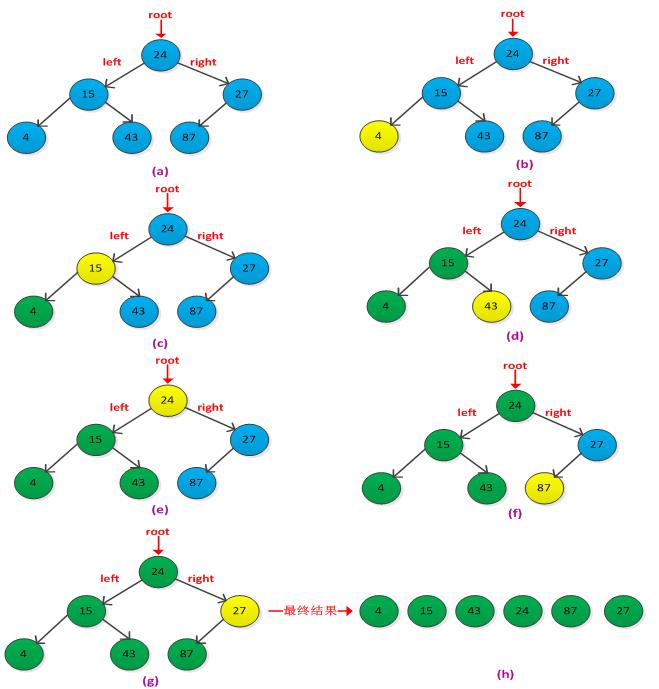
解答:这个题目在面试笔试中经常碰到,基本思想上将指针逆置。如下图所示:
(4)遍历单链表一次,找出链表中间节点。
解答:定义两个指针p和q,初始都指向链表头节点。然后开始向后遍历,p每次移动2步,q移动一步,当p到达末尾的时候,p正好到达了中间位置。
(5)用一个单链表L实现一个栈,要求push和pop的操作时间为O(1)。
解答:根据栈中元素先进后出的特点,可以在链表的头部进行插入和删除操作。
(6)用一个单链表L实现一个队列,要求enqueue和dequeue的操作时间为O(1)。
解答:队列中的元素是先进先出,在单链表结构中增加一个尾指针,数据从尾部插入,从头部删除。
3、有根树的表示
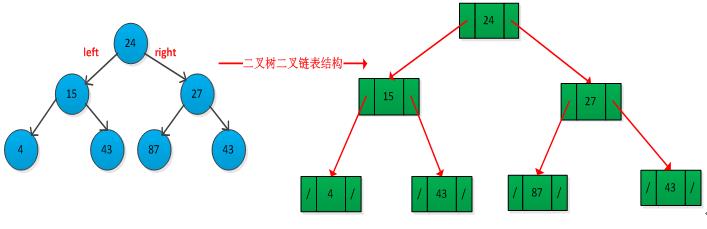
采用链表数据结构来表示树,书中先降二叉树的链表表示法,然后拓展到分支数无限制的有根数。先来看看二叉树的链表表示方法,用域p、left和right来存储指向二叉树T中的父亲、左孩子和右孩子的指针。如下图所示:

对于分支数目无限制的有根树,采用左孩子、右兄弟的表示方法。这样表示的树的每个节点都包含有一个父亲指针p,另外两个指针:
(1)left_child指向节点的最左孩子。
(2)right_sibling指向节点紧右边的兄弟。