前言:今天接着学习动态规划算法,学习如何用动态规划来分析解决矩阵链乘问题。首先回顾一下矩阵乘法运算法,并给出C++语言实现过程。然后采用动态规划算法分析矩阵链乘问题并给出C语言实现过程。

1 #include <iostream>
2 using namespace std;
3 #define A_ROWS 3
4 #define A_COLUMNS 2
5 #define B_ROWS 2
6 #define B_COLUMNS 3
7 void matrix_multiply(int A[A_ROWS][A_COLUMNS],int B[B_ROWS][B_COLUMNS],int C[A_ROWS][B_COLUMNS]);
8 int main()
9 {
10 int A[A_ROWS][A_COLUMNS] = {1,0,
11 1,2,
12 1,1};
13 int B[B_ROWS][B_COLUMNS] = {1,1,2,
14 2,1,2};
15 int C[A_ROWS][B_COLUMNS] = {0};
16 matrix_multiply(A,B,C);
17 for(int i=0;i<A_ROWS;i++)
18 {
19 for(int j=0;j<B_COLUMNS;j++)
20 cout<<C[i][j]<<" ";
21 cout<<endl;
22 }
23 return 0;
24 }
25 void matrix_multiply(int A[A_ROWS][A_COLUMNS],int B[B_ROWS][B_COLUMNS],int C[A_ROWS][B_COLUMNS])
26 {
27 if(A_COLUMNS != B_ROWS)
28 cout<<"error: incompatible dimensions."<<endl;
29 else
30 {
31 int i,j,k;
32 for(i=0;i<A_ROWS;i++)
33 for(j=0;j<B_COLUMNS;j++)
34 {
35 C[i][j] = 0;
36 for(k=0;k<A_COLUMNS;k++)
37 C[i][j] += A[i][k] * B[k][j]; //将A的每一行的每一列与B的每一列的每一行的乘积求和
38 }
39 }
40 }
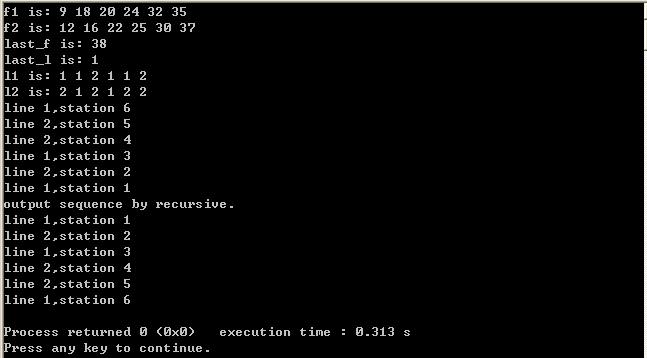
程序测试结果如下所示:

2、矩阵链乘问题描述
给定n个矩阵构成的一个链<A1,A2,A3,.......An>,其中i=1,2,...n,矩阵A的维数为pi-1pi,对乘积 A1A2...An 以一种最小化标量乘法次数的方式进行加全部括号。
注意:在矩阵链乘问题中,实际上并没有把矩阵相乘,目的是确定一个具有最小代价的矩阵相乘顺序。找出这样一个结合顺序使得相乘的代价最低。
3、动态规划分析过程
1)最优加全部括号的结构
动态规划第一步是寻找一个最优的子结构。假设现在要计算AiAi+1....Aj的值,计算Ai...j过程当中肯定会存在某个k值(i<=k<j)将Ai...j分成两部分,使得Ai...j的计算量最小。分成两个子问题Ai...k和Ak+1...j,需要继续递归寻找这两个子问题的最优解。
有分析可以到最优子结构为:假设AiAi+1....Aj的一个最优加全括号把乘积在Ak和Ak+1之间分开,则Ai..k和Ak+1..j也都是最优加全括号的。
2)一个递归解
设m[i,j]为计算机矩阵Ai...j所需的标量乘法运算次数的最小值,对此计算A1..n的最小代价就是m[1,n]。现在需要来递归定义m[i,j],分两种情况进行讨论如下:
当i==j时:m[i,j] = 0,(此时只包含一个矩阵)
当i<j 时:从步骤1中需要寻找一个k(i≤k<j)值,使得m[i,j] =min{m[i,k]+m[k+1,j]+pi-1pkpj} (i≤k<j)。
3)计算最优代价
虽然给出了递归解的过程,但是在实现的时候不采用递归实现,而是借助辅助空间,使用自底向上的表格进行实现。设矩阵Ai的维数为pi-1pi,i=1,2.....n。输入序列为:p=<p0,p1,...pn>,length[p] = n+1。使用m[n][n]保存m[i,j]的代价,s[n][n]保存计算m[i,j]时取得最优代价处k的值,最后可以用s中的记录构造一个最优解。书中给出了计算过程的伪代码,摘录如下:
1 MAXTRIX_CHAIN_ORDER(p)
2 n = length[p]-1;
3 for i=1 to n
4 do m[i][i] = 0;
5 for t = 2 to n //t is the chain length
6 do for i=1 to n-t+1
7 j=i+t-1;
8 m[i][j] = MAXLIMIT;
9 for k=i to j-1
10 q = m[i][k] + m[k+1][i] + qi-1qkqj;
11 if q < m[i][j]
12 then m[i][j] = q;
13 s[i][j] = k;
14 return m and s;
MATRIX_CHAIN_ORDER具有循环嵌套,深度为3层,运行时间为O(n3)。如果采用递归进行实现,则需要指数级时间Ω(2n),因为中间有些重复计算。递归是完全按照第二步得到的递归公式进行计算,递归实现如下所示:
1 int recursive_matrix_chain(int *p,int i,int j,int m[N+1][N+1],int s[N+1][N+1])
2 {
3 if(i==j)
4 m[i][j] = 0;
5 else
6 {
7 int k;
8 m[i][j] = MAXVALUE;
9 for(k=i;k<j;k++)
10 {
11 int temp = recursive_matrix_chain(p,i,k,m,s) +recursive_matrix_chain(p,k+1,j,m,s) + p[i-1]*p[k]*p[j];
12 if(temp < m[i][j])
13 {
14 m[i][j] = temp;
15 s[i][j] = k;
16 }
17 }
18 }
19 return m[i][j];
20 }
对递归算计的改进,可以引入备忘录,采用自顶向下的策略,维护一个记录了子问题的表,控制结构像递归算法。完整程序如下所示:
1 int memoized_matrix_chain(int *p,int m[N+1][N+1],int s[N+1][N+1])
2 {
3 int i,j;
4 for(i=1;i<=N;++i)
5 for(j=1;j<=N;++j)
6 {
7 m[i][j] = MAXVALUE;
8 }
9 return lookup_chain(p,1,N,m,s);
10 }
11
12 int lookup_chain(int *p,int i,int j,int m[N+1][N+1],int s[N+1][N+1])
13 {
14 if(m[i][j] < MAXVALUE)
15 return m[i][j]; //直接返回,相当于查表
16 if(i == j)
17 m[i][j] = 0;
18 else
19 {
20 int k;
21 for(k=i;k<j;++k)
22 {
23 int temp = lookup_chain(p,i,k,m,s)+lookup_chain(p,k+1,j,m,s) + p[i-1]*p[k]*p[j]; //通过递归的形式计算,只计算一次,第二次查表得到
24 if(temp < m[i][j])
25 {
26 m[i][j] = temp;
27 s[i][j] = k;
28 }
29 }
30 }
31 return m[i][j];
32 }
4)构造一个最优解
第三步中已经计算出来最小代价,并保存了相关的记录信息。因此只需对s表格进行递归调用展开既可以得到一个最优解。书中给出了伪代码,摘录如下:
1 PRINT_OPTIMAL_PARENS(s,i,j)
2 if i== j
3 then print "Ai"
4 else
5 print "(";
6 PRINT_OPTIMAL_PARENS(s,i,s[i][j]);
7 PRINT_OPTIMAL_PARENS(s,s[i][j]+1,j);
8 print")";
4、编程实现
采用C++语言实现这个过程,现有矩阵A1(30×35)、A2(35×15)、A3(15×5)、A4(5×10)、A5(10×20)、A6(20×25),得到p=<30,35,15,5,10,20,25>。实现过程定义两个二维数组m和s,为了方便计算其第一行和第一列都忽略,行标和列标都是1开始。完整的程序如下所示:
1 #include <iostream>
2 using namespace std;
3
4 #define N 6
5 #define MAXVALUE 1000000
6
7 void matrix_chain_order(int *p,int len,int m[N+1][N+1],int s[N+1][N+1]);
8 void print_optimal_parents(int s[N+1][N+1],int i,int j);
9
10 int main()
11 {
12 int p[N+1] = {30,35,15,5,10,20,25};
13 int m[N+1][N+1]={0};
以上是关于《算法导论》读书笔记的主要内容,如果未能解决你的问题,请参考以下文章