线段树

Posted 2020-10-25 peppa

【线段树是啥】

本人的理解：一颗由“线段”构成的二叉树，每个“线段”中存了一些数（按照大小排好的）附图：

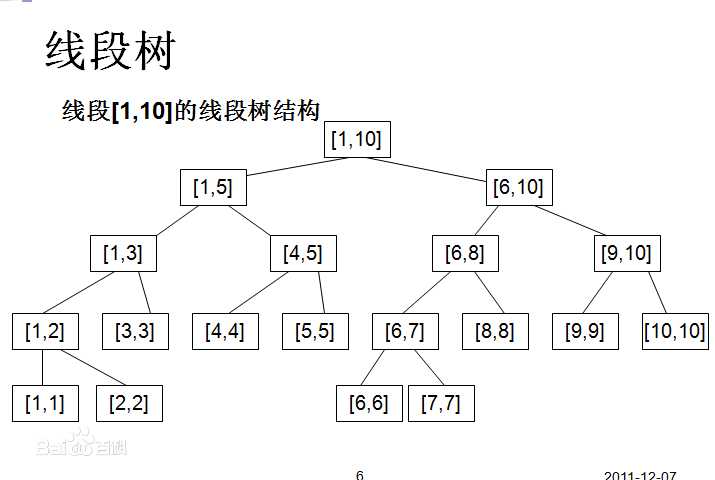
上图中每个闭区间可以看成一个线段。以根节点这位老父亲为例：它的左儿子存了他的左半段，它的右儿子存了它的右半段。

再看像最底下那层那样的（原谅我这个一点不专业的说法），闭区间左端的数和右端的数是相同的，把它称作元线段。

线段树的原理理解起来挺简单，但代码对于我这个弱鸡来说简直是无情的斩杀。   

【贴板子】

 1 struct line
 2 {
 3     int left,right;//线段左端点、右端点 
 4     int n;//凡是匹配，记录+1，默认为0
 5 }a[100];
 6 void build(int l,int r,int n)//建树 ，n为结点序号 
 7 {
 8     int mid = l / 2 + r / 2;
 9     a[n].left = l;
10     a[n].right = r;
11     if(r == l) return;
12     a[n].left = l;
13     a[n].right = r;
14     build(l,mid,2*n);
15     build(mid+1,r,2*n+1);
16  }
17 void insert(int l,int r,int step)//l,r为插入的元素，step某条线段的下标（结点序号） 
18 {
19      if(l == a[step].left && r == a[step].right)
20      {
21          a[step].n++;//插入的线段匹配则此条线段的记录+1
22         return; //插入结束返回 
23      }
24      if(a[step].left == a[step].right) 
25          return;//左端和右端的数值相等？！表示它是个元线段，插入结束返回 
26      int mid = a[step].left / 2 + a[step].right / 2;//当前线段的中点 
27      if(mid >= r) 
28          insert(l,r,step*2);//如果中点在r的右边，则应该插入到左儿子 
29      else if(mid < l) 
30          insert(l,r,step*2+1);//如果中点在l的左边，则应该插入到右儿子
31      else//否则，中点是在l，r之间，把待插线段分成两半分别插到左右儿子里面
32      {
33           insert(l,mid,step*2);
34           insert(mid+1,r,step*2+1); 
35     }
36 }
37 void count(int l,int r,int step)//访问，这个上面插入元素的方法一样。 
38 {
39     if(a[step].n != 0) sum+=a[step].n * (t - s + 1);
40     if(a[step].left == a[step].right) return;
41     int mid = a[step].left / 2 + a[step].right / 2;
42         if (mid>=t)
43     count(s,t,step*2);
44     else
45     if (mid<s)
46     count(s,t,step*2+1);
47     else
48     {
49         count(s,mid,step*2);
50         count(mid+1,t,step*2+1);
51     }
52 }

以上操作均是递归过程

至于什么专业的名词、定义，可以百度百科。

【一些解读】 “每次匹配，记录加一”的意思就是比如说你要插入一条线段，把它分分分，找到了个地方插进去，这个时候你插入的l，r元素与线段的左右端点的元素相等，这是正好匹配，所以记录加一。

【一些单词】

line--线

inserve--插入

build--建立

【Orz】日常求鄙视，错误不足之处求指点