前言
这是一道cf的比赛题..
比赛的时候C题因为自己加了一个很显然不对的特判WA了7次但找不出原因就弃疗了...
然后就想划水, 但是只做了AB又不太好... 估计rating会掉惨 (然而事实证明rating一点没变)
就去看看别的题,, 但是英语不好, 看题要看半天, 看看这个E题题目名称像是数论?(mmp估计是受到了古代猪文的影响). 点进去没仔细读题好像是个等价表达式一样的题目? 好像很麻烦还1h不写了(没错C题细节各种挂调了好久好久, 当时已经是很绝望了OvO)
结果这题tm是个dp...
题意
英文题一定要有的一个部分... 毕竟
这么长时间不学, 还会说英语吗? ——wcg
所以还是要翻译一下...
就是给一个运算符都被扣掉的表达式, 让你往里面填\\(P\\)个\\(+\\)和\\(M\\)个\\(-\\), 求最大的可能的结果.
表达式中的数字都是一位数, 而且每一层运算都套了一个括号, (这样才比较方便处理, 其实麻烦一点也能处理但是...)
分析
显然地, 我们可以把表达式画成一棵树. 以第四组样例为例, 我们可以画出一棵这样的树:
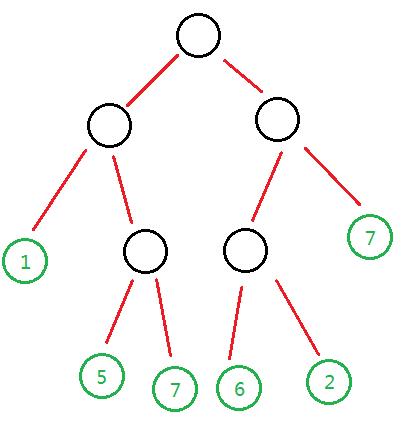
然后怎么建树啊, 我们知道这棵树肯定是从底往上建的, 所以我们要利用一种神奇的, 叫"栈"的数据结构.
我们用一个临时变量tmp来储存等待着父亲的左儿子. 这个左儿子可能是一个数, 也可能是一个点. 为了方便起见, 我们让点的标号从11开始(因为数字只有一位...那你说为什么不用10呢?).
- 当我们扫到一个数字的时候, 把tmp设置为这个数字.
- 当我们扫到一个?的时候, 我们建立一个新节点(其实就是++tot就行了), 将tmp作为他的左儿子, 右儿子先留空.
然后将其入栈, 表示接下来的一个右儿子应该去找它. - 当我们遇到一个)的时候, 我们将tmp作为栈顶元素的右儿子. 然后将tmp设置为栈顶元素, 栈顶元素出栈.
发现自己并不能解释清楚为什么要这么搞... 自己画画图体会一下吧OvO.
建好树后我们来设计状态:
- 令\\(f[x][i]\\)表示在以\\(x\\)为根的子树中使用了\\(i\\)个\\(+\\)得到的最大值
- 由于有-的存在, 我们令\\(g[x][i]\\)表示在以\\(x\\)为根的子树中国使用了\\(i\\)个\\(+\\)得到的最小值
然后我们就记忆化搜索一波, 枚举\\(+\\)的个数做就行了, 对于当前节点:
-
这个节点是个数字? 直接返回咯~
-
两个儿子都是数字? 直接算咯~
-
填\\(+\\):
f[x][i]=max{f[lson[x]][j]+f[rson[x]][i-j-1]},j=0..i-1
左右两儿子都取最大时和最大
g[x][i]=min{g[lson[x]][j]+g[rson[x]][i-j-1]}
左右两儿子都取最小时和最小 -
填\\(-\\):
f[x][i]=max{f[lson[x]][j]-g[rson[x]][i-j-1]}
左儿子取最大, 右儿子取最小时差最大
g[x][i]=min{g[lson[x]][j]-f[rson[x]][i-j-1]}左儿子取最小, 右儿子取最大时差最小.
这样就做完了(假的), 时间复杂度\\(O(n*P)\\), 可能会过不了.
而且空间复杂度也是\\(O(n*P)\\)的, 数组应该开不开..
但是呢\\(min(P,M)\\leq100\\), 这样我们就可以分类讨论一下, 然后用上面的做法只枚举较少的那个符号...
这样时空复杂度就都能过辣...
代码(写的有点丑,没怎么压行,calcMax和calcMin基本是一样的...):
#include <cctype>
#include <cstdio>
#include <cstring>
const int INF=1000000007;
inline int max(const int &a,const int &b){return a>b?a:b;}
inline int min(const int &a,const int &b){return a<b?a:b;}
int t[5015][2],f[5005][102],g[5005][102],sz[5005];
int stk[5005],tp,cur,tot=10,rt;
char str[10010]; bool now;
void dfssz(int x){ //用子树中包含运算符的个数来排除一部分不合法状态.
sz[x]=1;
if(t[x][0]>10) dfssz(t[x][0]),sz[x]+=sz[t[x][0]];
if(t[x][1]>10) dfssz(t[x][1]),sz[x]+=sz[t[x][1]];
}
void init(){ //建树
memset(f,192,sizeof(f));
memset(g,127,sizeof(g));
int l=strlen(str),fa;
for(int i=0;i<l;++i){
if(isdigit(str[i]))
cur=str[i]-\'0\';
if(str[i]==\'?\'){
stk[++tp]=++tot;
t[tot][0]=cur;
}
if(str[i]==\')\'){
fa=stk[tp--];
t[fa][1]=cur;
cur=rt=fa;
}
}
dfssz(rt);
}
int calcMax(int x,int p);
int calcMin(int x,int p){
if(p<0||p>sz[x]) return INF;
if(x<10) return x;
if(sz[x]==1) return now==(bool)p?t[x][0]+t[x][1]:t[x][0]-t[x][1];
if(g[x][p]<INF) return g[x][p];
int mn=min(sz[t[x][0]],p),ans1,ans2;
for(int i=0;i<=mn;++i){
ans1=calcMin(t[x][0],i)+calcMin(t[x][1],p-now-i); //+
ans2=calcMin(t[x][0],i)-calcMax(t[x][1],p+now-1-i); //-
g[x][p]=min(g[x][p],min(ans1,ans2));
}
return g[x][p];
}
int calcMax(int x,int p){
if(p<0||p>sz[x]) return -INF;
if(x<10) return x;
if(sz[x]==1) return now==(bool)p?t[x][0]+t[x][1]:t[x][0]-t[x][1];
if(f[x][p]>-INF) return f[x][p];
int mn=min(sz[t[x][0]],p),ans1,ans2;
for(int i=0;i<=mn;++i){
ans1=calcMax(t[x][0],i)+calcMax(t[x][1],p-now-i); //+
ans2=calcMax(t[x][0],i)-calcMin(t[x][1],p+now-1-i); //-
f[x][p]=max(f[x][p],max(ans1,ans2));
}
return f[x][p];
}
int main(){
scanf("%s",str);
if(strlen(str)==1){puts(str);return 0;}
init();
int a,b; scanf("%d%d",&a,&b);
if(a<b) now=1; else now=0; //now用来标记+多还是-多
printf("%d",calcMax(rt,now?a:b));
}
过了一个假期颓成狗了... 代码都不会写了快...
啊啊啊啊啊下午还要测试怎么办啊~