二叉搜索树

Posted 2020-10-24 Ivan B.G. Liu

1.  二叉搜索树，又称BST。满足三个性质：

          （1）若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

          （2）若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

          （3）它的左、右子树也分别为二叉排序树。

            

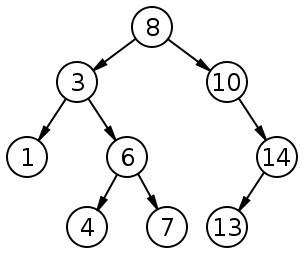
2. 二叉搜索树的遍历：

        前序：先根节点，再左子树，后右子树

        中序：先左子树，再根节点，后右子树

        后序：先左子树，再右子树，后根节点

        遍历的时间复杂度是：O（n），代码如下：

/*前序遍历*/
void PreOrderTraverse(shared_ptr<node> &root)
{
    if(root != NULL)
    {
        cout<<root->val<<" ";
        PreOrderTraverse(root->left);
        PreOrderTraverse(root->right);    
    }
}

/*中序遍历*/
void InOrderTraverse(shared_ptr<node> &root)
{
    if(root != NULL)
    {
        InOrderTraverse(root->left);
        cout<<root->val<<" ";
        InOrderTraverse(root->right);
    }
}

/*后序遍历*/
void PostOrderTraverse(shared_ptr<node> &root)
{
    if(root != NULL)
    {
        PostOrderTraverse(root->left);
        PostOrderTraverse(root->right);
        cout<<root->val<<" ";
    }
}

 

3. 二叉搜索树的查找：

   由于二叉搜索树是已经排序好的树，所以其查找算法只需从树顶点开始向下遍历节点即可。时间复杂度是O(h)。代码如下：

Treenode * search（Treenode *root，int ele）
{
    if(root != NULL)
    {    
        if(root->val == ele)
            return root;
        else if(root->val > ele)
            return search(root->left,ele);
        else if(root->val < ele)
            return search(root->right,ele);
    }
    else
        return NULL;
}

 

4. 二叉搜索树的插入：

    由于插入的任意节点都在树的叶节点，这样使得插入时，不必移动其他节点，只要改动某个节点的指针，将其从空节点变为非空即可。时间复杂度是：O(h)。代码如下：

Treenode * insert（Treenode *root，int ele）
{
    Treenode *preroot = NULL;
    //找到ele落位的叶节点位置
    while(root)
    {
        preroot = root;
        if(root->val > ele)
            root = root->left;
        else
            root = root->right;
    }
    if(preroot == NULL)            //说明是空树
        root = new Treenode(ele);
    else if(preroot->val > ele)    //插入到左边
        preroot->left = new Treenode(ele);
    else                           //插入到右边
        preroot->right = new Treenode(ele);
}

 

5. 二叉搜索树的删除：

    节点的删除分为几种情况：

    （a）当该节点为叶子节点，则让该节点的父节点指向其变为NULL，然后释放节点；

    （b）当该节点不是叶子节点，但左子树或者右子树为空，则：

            （1）若左子树为空，则让该节点父节点指向其右节点；

            （2）若右子树为空，则让该节点父节点指向其左节点。

    （c）当该节点不是叶子节点，且左子树和右子树都不为空，则：

            （1）在该节点的左子树中找到最大节点Lmax（该节点必然是一个叶子节点），取出Lmax的值val，删除Lmax；

            （2）将 val 赋给该节点的值，即：root->val = val。

            （3）判断Lmax的父节点PreLmax的左节点是否等于Lmax，若是则：

                               PreLmax->left = Lmax->left    否则：  PreLmax->right = Lmax->left

      二叉搜索树的删除复杂度为O（h），h是二叉树的高度。代码如下：

/*删除二叉搜索树中的指定值的节点*/
node *deleteNode(node *root, int ele)
{
    node *newroot = root;  //指向新的根节点 
    node *presite = root; //指向要删除节点的父节点 
    int pos = 0; //要删除节点在其父节点的位置： -1：在左侧    1：在右侧    0：就是根节点  
    /*找到要删除的元素在BST中的位置*/ 
    while(root != NULL)
    {
        if(root->val > ele)
        {
            presite = root;
            root = root->left;
            pos = -1;
        }
        else if(root->val < ele)
        {
            presite = root;
            root = root->right;
            pos = 1;
        }
        else
        {
            break;            
        }
    }
    if(root == NULL)
    {
        cerr<<"要删除的节点不存在于BST中\\n";
    }
    else
    {
        //该节点有左子树和右子树 
        if(root->left!=NULL && root->right!=NULL)
        {
            cout<<"has left and right tree\\n";
            node *Lmax = root->left;    //最大左子节点 
            node *PreLmax = root;       //最大左子节点的父节点 
            while(Lmax->right != NULL)
            {
                PreLmax = Lmax;     
                Lmax = Lmax->right;
            }
            root->val = Lmax->val;　　  //替换root的值为最大左子树节点值
            if(PreLmax->left == Lmax)  //root的左子树最大节点是root的左节点 
                PreLmax->left = Lmax->left;
            else　　　　　　　　　　　　　　//root的左子树最大节点不是root的左节点
                PreLmax->right = Lmax->left;
            delete Lmax;
            Lmax = NULL;
        }
        //该节点的左子树为空 
        else if(root->left == NULL && root->right != NULL)      
        {
            cout<<"left tree is empty\\n";
            if(0 == pos)        //在根节点 
            {
                newroot = root->right;
            }
            else if(1 == pos)     //在右侧 
            {    
                presite->right = root->right;
            }
            else                  //在左侧 
            {
                presite->left = root->right;    
            }
            delete root;
            root = NULL;
        }
        //该节点的右子树为空 
        else if(root->right == NULL && root->left != NULL)     //site的右子树为空
        {
            cout<<"right tree is empty\\n";
            if(0 == pos)      //在根节点 
            {
                newroot = root->left;
            }
            else if(1 == pos) //在右侧 
            {
                presite->right = root->left;
            }
            else                //在左侧 
            {
                presite->left = root->left;    
            }
            delete root;
            root = NULL;
        }
        //该节点为叶子节点 
        else                    
        { 
            cout<<"leaf node\\n";
            if(0 == pos)          //根节点 
            {
                cerr<<"BST只有一个节点且被删除，该BST变为空树\\n";
                delete root;
                root = NULL;
            }
            else if(1 == pos)      //在右侧 
            {
                presite->right = NULL;
                delete root;
                root = NULL;
            }
            else                  //在左侧 
            {
                presite->left = NULL;
                delete root;
                root = NULL;    
            }
        }    
    }
    return newroot;
}