Optimization algorithms
优化算法以加速训练。
Mini-batch gradient descend
- Batch gradient descend:每一小步梯度下降否需要计算所有的训练样本。很耗时。
- Mini-batch gradient descend:将训练集分为很多小的mini-batch,每一个epoch用到一个mini-batch的训练样本,进行一次梯度下降(向前传播,计算cost,向后传播)。训练速度会提升很多。
选择mini-batch的size
-
如果size=1:随机梯度下降,过程会曲折反复,不收敛,在最优值附近徘徊(紫色线)。一个很大的缺点在于每次只处理一个样本,失去了向量化的提升效率的作用。
-
如果size=m:批梯度下降,过程比较直接但是每步都很耗时。(蓝色线)
-
size适中,则可以既利用到向量化的作用,又每一步下降不需要耗时过长,因此效率较高。(绿色线)

size选择大致原则:
- 如果训练集很小(如m <= 2000):Batch gradient descend
- 如果训练集相对大,那么典型的mini-batch的大小如:64,128,256,512。考虑到计算机的内存,所以常用的mini-batch都是2的次方。
- 确保mini-batch和计算机CPU/GPU的内存相适应。
mini-batch size是需要调整的超参数之一,尝试不同的值,然后选择一个最好的。
补充知识:Exponentially weighted averages(指数加权平均)
以每日温度的指数加权平均计算为例,每天的温度值如蓝色点所示,数据看起来噪声比较大,如下图。
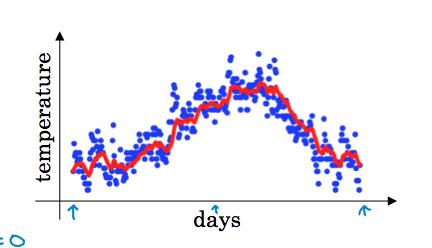
我们计算数据的趋势,即温度的局部平均,使用指数加权平均。计算公式为:
其中,\\(v_t\\)表示t天温度的指数加权平均值,\\(\\theta_t\\)表示当天的温度值,β是参数。
实际上,\\(v_t\\)可以看作约等于取前\\(\\frac {1}{1 - \\beta}\\)天的平均值。
例如取β = 0.9,我们得到红色的线;当取β = 0.98时,得到绿色线。注意到,当β的值很大(接近1)时,线条会更加的平滑,因为对更多的天数取了平均值,但是会有更多的延迟出现,因为计算过去的权重很大而当前的权重很小,对变化的适应更迟缓。而另一个极端值,如β = 0.5时,则得到噪声较大的黄色线。
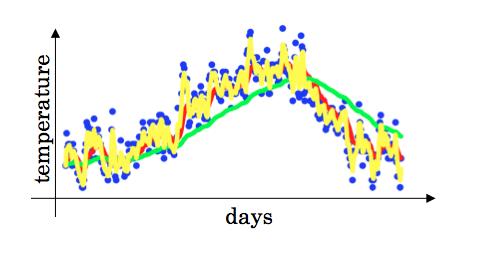
对指数加权平均的理解
我们假设β = 0.9,对\\(v_100\\)进行展开,得到图中表达式,每天温度的权值指数衰减,且和近似为1,实际上可以看作是将原来的数据和一个指数衰减函数对应相乘。注意到\\(0.9^{10} \\approx 0.35 \\approx \\frac {1}{e}\\),即10天以外的温度值的权重很小,因此可以近似看作只关心最近的前十天的平均值,这是一种经验之谈。

应用指数加权平均
Set v_θ = 0
Repeat
{
Get next θ_t
v_θ := βv_θ + (1-β)θ_t
}
虽然不是最准确的平均值,但是节省储存空间。
Bias correction
我们发现按照公式实际计算时候,如当取β = 0.98时,无法绿色线,而是紫色线,它的起始值很低,这是因为\\(v_0 = 0\\),而在起始的几天的权值都很低。
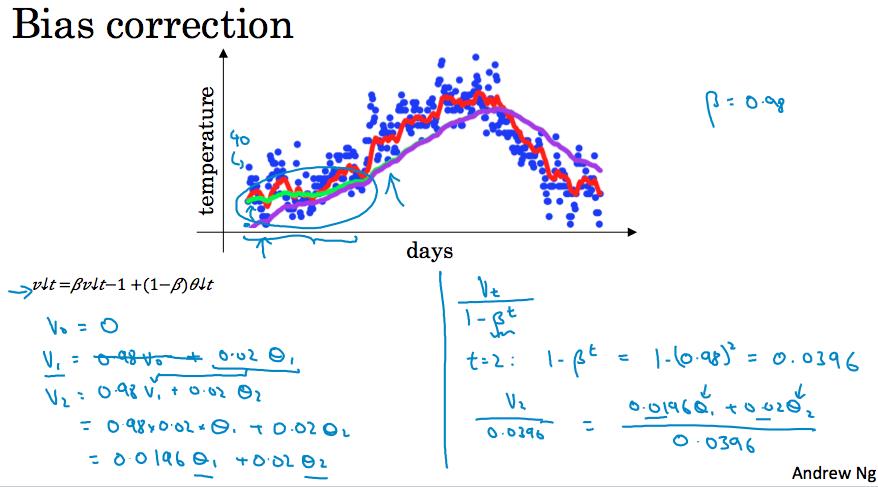
我们进行误差修正,用\\(\\frac{v_t}{1 - \\beta^t}\\)代替,可以帮助进行更好的估计。
(未完待续)