【题目描述】
长度为n的环状串有n种表示法,分别为某个位置开始顺时针得到。例如,图中的环状串有10种表示:
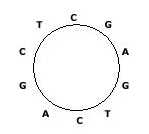
CGAGTCAGCT,GAGTCAGCTC,AGTCAGCTCG等。在这些表示法中,字典序最小的称为“最小表示”。
输入一个长度为n(n<=100)的环状DNA串(只包含A、C、G、T这4种字符)的一种表示法,你的任务是输出该环状串的最小表示。例如,CTCC的最小表示是CCCT,CGAGTCAGCT的最小表示为AGCTCGAGTC.
输入:
在输入文件的第一行 为序列数量。每一个测试用例都需要一行包含一个循环序列,这个序列被写成一个任意的线性序列。由于循环序列是DNA串,只有四个符号:A,C,G,T。每一序列的长度为n(2<=n<=100)。
输出:
每行为串的字典序最小的序列。下面的样例为2个串的序列。
【样例输入】
2
CGAGTCAGCT
CTCC
【样例输出】
AGCTCGAGTC
CCCT
【代码实现】
1 #include <stdio.h> 2 #include <string.h> 3 4 #define MAX (int)1e2 + 10 5 6 int Isless( const char s[], int i, int start) 7 { 8 int len = strlen(s); 9 printf ("%d\\n", len); 10 for ( int j = 0; j < len; j ++) 11 if ( s[(i+j)%len] != s[(start+j)%len]) 12 return s[(i+j)%len] < s[(start+j)%len]; 13 return 0; 14 } 15 16 int main() 17 { 18 char s[MAX]; 19 while ( scanf ("%s", s) == 1 ) { 20 int start = 0; 21 int n = strlen(s); 22 for ( int i = 1; i < n; i++ ) { 23 if ( Isless(s, i, start) ) start = i; 24 } 25 for ( int i = 0; i < n; i++ ) { 26 printf ("%c", s[(start + i) % n]); 27 } 28 printf ("\\n"); 29 } 30 31 return 0; 32 }
【总结】
自己想的有点复杂,没能写出来。。直接看的书,但书上题目描述不像上面那样详细,所以对具体输入的实现有些差别。但核心是一样的:下标0~n-1,找到最小字典序的起始位置。只要当前下标的字典序小于之前的,就将它用 start 记录下来,即不断更新 start 。有点类似于一组数中找最小值,只是比较方法单写了一个自定义函数罢了。
其中自定义函数形参表中的 const char* s 是个新的启发,如果写成 char s[] 则会有两点问题:
1. 定义不够准确,自定义函数中并不会对数组s进行修改,所以类型至少应该为 const char ;
2. 如果是形参为数组s[ ],则在函数内无法使用 sizeof 来求出数组长度,而定义为指针则不会有这个麻烦(虽然本题中使用的是 strlen() )。
对于循环数组的下标处理,在循环队列的数组实现时已经学过,但是又忘了。。这回再捡起来:对数组长度取模!