博弈论
Posted TQCAI
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了博弈论相关的知识,希望对你有一定的参考价值。
1.三国游戏(完全信息静态博弈)
代码:

#include <stdio.h> #include <memory.h> #include <math.h> #include <string> #include <vector> #include <set> #include <stack> #include <queue> #include <algorithm> #include <map> #define I scanf #define OL puts #define O printf #define F(a,b,c) for(a=b;a<c;a++) #define FF(a,b) for(a=0;a<b;a++) #define FG(a,b) for(a=b-1;a>=0;a--) #define LEN 1000 #define MAX 1<<30 #define V vector<int> using namespace std; int a[LEN][LEN]; int main(){ // freopen("D:\\\\CbWorkspace\\\\博弈论\\\\三国游戏.txt","r",stdin); int i,j,n; I("%d",&n); for(i=1;i<=n;i++){ a[i][i]=-1; for(j=i+1;j<=n;j++){ I("%d",&a[i][j]); a[j][i]=a[i][j]; } } //对于每一个英雄,进行排序 for(i=1;i<=n;i++) sort(a[i]+1,a[i]+1+n); //在第二小的value中寻找 int ans=-1; for(i=1;i<=n;i++) ans=max(ans,a[i][n-1]); printf("%d\\n%d\\n",1,ans); i=0; return 0; }
排序前:
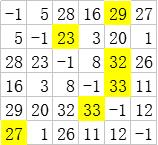
排序后:
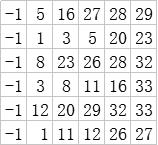 (排序取第n-1最大值的目的:拿到最大的次大值)
(排序取第n-1最大值的目的:拿到最大的次大值)
理解:
每个武将对应的所有配对值中最大的值,已经被拆散在这种情况下,场上存在的只剩所有的“次大值”,就是我们拿来排序的那一堆。
这时候小涵拿到了“次大值”中的最大值,肯定是场上最高的分数。
1.从武将中找出武将i,记下与i的默契值第二大的武将j,使得i与j的默契值最大(在第二大的列里面最大。这就是排序取n-1的意义)
2.小涵选出i,那么计算机只会选出与i默契值最大的武将p
此时与p的默契值最大值一定是i。
因此,我们第一次选了i,取得了次大值中的最大值,同时拆掉了i的最大值和p的最大值。
以上是关于博弈论的主要内容,如果未能解决你的问题,请参考以下文章
