约数和（神奇的数列优化）

Posted 2020-10-24 66t6

题目大意

求区间[x，y]中所有元素的因数和（x<=y）

思路

如果这道题太难了，来看看另一道简单的题：

给你很多个数N，需要你算出这些数所有约数的和。（N的约数指能整除N的正整数），例如12的约数有1,2,3,4,6,12。所以约数和为1+2+3+4+6+12=28。

（1）50分的代码，打表实现

#include<cstdio>
const int maxn=5000010;
int t,n,s[maxn];
int main(){
    for(int i=1;i<=maxn;i++)
    for(int j=i;j<=maxn;j+=i)
    s[j]+=i;
    scanf("%d",&t);
    while(t--){
        scanf("%d",&n);
        printf("%d\\n",s[n]);
    }
    return 0;
}

View Code

（2）枚举+卡常数+记忆化

#include<bits/stdc++.h>
using namespace std;
inline const int read(){
    register int x=0,f=1;
    register char ch=getchar();
    while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();}
    while(ch>=‘0‘&&ch<=‘9‘){x=(x<<3)+(x<<1)+ch-‘0‘;ch=getchar();}
    return x*f;
}
int T,v,f[100000010];
inline int go(){
    int i,sum=0;
    for(i=1;i*i<v;i++)
        if(v%i==0) sum+=i+v/i;
    if(i*i==v) sum+=i;
    return sum;
}
int main(){
    T=read();
    while(T--){
        v=read();
        if(!f[v]) f[v]=go();
        printf("%d\\n",f[v]);
    }
    return 0;
}

View Code

虽然并没有什么卵用

但我们可以冷静下来想一想

既然本题求的是区间约数和，我们首先想到的方法就是用前缀和的思想，ans [x~y]=ans[1~y] – ans[1~x-1]

求1~n的约数和，用的是这种方法：

1:1/2=0           sum=1

2:2/2=1 2/3=0      sum=1*2+2=4

3:3/2=1 3/3=1 3/4=0  sum=1*3+1*2+3=8

4:4/2=2 4/3=1 4/4=1  sum=2*2+1*3+1*4+4=15

它的正确性很好证明

n/a的值就是1~n这些数中以a为因数的数的个数，再乘以a即因数和

最后加上n是由于n本身是n的因数

所以Σ(i=1,n)n/i*i就是结果

然后我们就有了60分的代码（why，也许你想问）

#include<iostream>
using namespace std;
long long l,r,al,ar;
long long work(long long a){
    long long result=0;
    for(long long i=2;i<=a;i++){
        if(a/i==0)break;
        result+=(a/i)*i;
    }
    result+=a;
    return result;
}
int main(){
    cin>>l>>r;
    al=work(l-1);
    ar=work(r);
    cout<<ar-al;
}

View Code

很明显这种方法会超时呢（美丽的TLE）

但其实这题思路是没毛病的，但是TLE的问题说明代码需要优化加速（怎么加，你告诉我）

用等差数列优化

首先根据之前的发现，以4为例，会发现4/3=1,4/4=1，到待除的除数较大时以a为因数的数的个数会呈现很长一段的相等局面，同样的，在别的数字上也会出现类似的情况，而且数字越大，这种情况的出现越多，我把3,4分别叫做本例中情况的左右边界。而且不难发现这种情况的连续序列中的a都是等差的，差为一，所以可以直接利用等差数列求和（这么巧！！！）

就是下面这个弱智的小学生公式

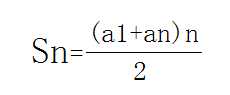
所以我们只需要枚举一下左右边界即可

代码就不给了啊