最大权闭合子图,神题
这不是线性代数,这是网络流。
我们看见这是一堆矩阵的运算,而且最后变成了一个数,那么我们就想到,把这个矩阵乘法的过程用具体的数字推出来
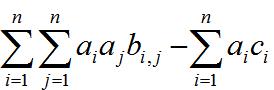
我们发现,a是一个01矩阵,然后其实就可以化成这么一个问题:
有n个东西,选了i,j两件东西能得到b[i,j]的价值,然而选i需要c[i]的花费,选j需要c[j]的花费……
这是一个经典的最小割模型,最大权闭合子图,详见胡伯涛论文。
建立S,T。
S连(i,j)边,边权为b[i,j],(i,j)连i、连j边,边权均为∞,i向T连边,边权为c[i]。
然后求最小割,最后答案就是
sum(b[i][j])-最小割答案 (i∈[1..n],j∈[1..n])
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <bitset>
#include <queue>
#define inf 0x3f3f3f3f
using namespace std;
const int MAXN = 300005;
int n, b[505][505], c[505], s, t, head[MAXN], nume, MaxFlow, ans, dep[MAXN], cur[MAXN];
int init() {
int rv = 0, fh = 1;
char c = getchar();
while(c < \'0\' || c > \'9\'){
if(c == \'-\') fh = -1;
c = getchar();
}
while(c >= \'0\' && c <= \'9\'){
rv = (rv<<1) + (rv<<3) + c -\'0\';
c = getchar();
}
return fh * rv;
}
struct edge{
int to, nxt, flow, cap;
}e[MAXN<<4];
void adde(int from, int to, int cap){
e[++nume].to = to;
e[nume].nxt = head[from];
e[nume].cap = cap;
head[from] = nume;
}
queue <int> q;
bool bfs(){
q.push(s);
memset(dep,0,sizeof(dep));
dep[s]=1;
while(!q.empty()){
int u = q.front();q.pop();
for(int i = head[u] ; i ; i = e[i].nxt){
int v = e[i].to;
if(!dep[v]&&e[i].flow < e[i].cap){
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return dep[t];
}
int dfs(int u, int flow) {
if(u == t) return flow;
int tot = 0;
for(int &i = cur[u] ; i&&tot < flow ; i = e[i].nxt) {
int v = e[i].to;
if(dep[v] == dep[u] + 1&&e[i].flow < e[i].cap) {
if(int t = dfs(v, min(e[i].cap - e[i].flow, flow - tot))) {
tot += t;
e[i].flow += t;
e[((i-1) ^ 1 ) + 1].flow -= t;
}
}
}
return tot;
}
void dinic(){
while(bfs()) {
memcpy(cur,head,t*4+4);
MaxFlow+=dfs(s, 0x3f3f3f3f);
}
}
int main() {
freopen("in.txt", "r", stdin);
n=init();
for(int i = 1 ; i <= n ; i++) {
for(int j = 1; j <= n; j++) {
b[i][j] = init();
ans += b[i][j];
}
}
for(int i = 1;i <= n;i++){
c[i]=init();
}
s=0;t=n*n+n+1;
for(int i = 1;i <= n ;i++){
for(int j = 1;j <= n;j++){
adde(s,i*n+j-n,b[i][j]);
adde(i*n+j-n,s,0);
}
}
for(int i = 1;i <= n;i++) {
adde(n*n+i, t, c[i]);
adde(t, n*n+i, 0);
}
int kkk=n*n;
for(int i = 1;i <= n ;i++) {
int ttt=i*n-n;
for(int j=1 ;j <=n ;j++) {
adde(ttt+j,kkk+i,inf);
adde(kkk+i,ttt+j,0);
adde(ttt+j,kkk+j,inf);
adde(kkk+j,ttt+j,0);
}
}
dinic();
cout<<ans-MaxFlow<<endl;
fclose(stdin);
return 0;
}