哈密顿图的判定
Posted 日拱一卒 功不唐捐
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了哈密顿图的判定相关的知识,希望对你有一定的参考价值。
推荐学习资料:
http://www.cnblogs.com/Ash-ly/p/5452580.html
http://ylroki.blog.163.com/blog/static/162978871201032775322518/
https://wenku.baidu.com/view/38dd0d4714791711cd791725.html
一、定义
通过图G的每个节点一次,且仅一次的通路称为哈密顿通路
通过图G的每个节点一次,且仅一次的回路称为哈密顿回路
含有哈密顿回路的图称为哈密顿图
二、哈密顿图的性质与判定
摘自:https://wenku.baidu.com/view/38dd0d4714791711cd791725.html



三、哈密顿回路的构造
摘自:http://ylroki.blog.163.com/blog/static/162978871201032775322518/

四、哈密顿回路的构造代码
输出哈密顿图的一条哈密顿回路

#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define N 401 int n,m; bool e[N][N]; int cnt,s,t; bool vis[N]; int ans[N]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-\'0\'; c=getchar(); } } void Reverse(int i,int j) { while(i<j) swap(ans[i++],ans[j--]); } void expand() { while(1) { int i; for(i=1;i<=n;++i) if(e[t][i] && !vis[i]) { ans[++cnt]=t=i; vis[i]=true; break; } if(i>n) return; } } void Hamilton() { memset(vis,false,sizeof(vis)); cnt=0; s=1; for(t=1;t<=n;++t) if(e[s][t]) break; vis[s]=vis[t]=true; cnt=2; ans[1]=s; ans[2]=t; while(1) { expand(); Reverse(1,cnt); swap(s,t); expand(); if(!e[s][t]) { int i; for(i=2;i<cnt;++i) if(e[ans[i]][t] && e[s][ans[i+1]]) break; t=ans[i+1]; Reverse(i+1,cnt); } if(cnt==n) break; int j,i; for(j=1;j<=n;++j) if(!vis[j]) { for(i=2;i<cnt;++i) if(e[ans[i]][j]) break; if(e[ans[i]][j]) break; } s=ans[i-1]; Reverse(1,i-1); Reverse(i,cnt); ans[++cnt]=j; t=j; vis[j]=true; } for(int i=1;i<=cnt;++i) printf("%d ",ans[i]); printf("%d\\n",ans[1]); } int main() { int u,v; while(1) { read(n); read(m); if(!n) return 0; memset(e,false,sizeof(e)); while(m--) { read(u); read(v); e[u][v]=e[v][u]=true; } Hamilton(); } }
五、竞赛图上的哈密顿通路
定理:竞赛图一定存在哈密顿通路。竞赛图的任意导出子图也一定存在哈密顿通路
采用数学归纳法,假设现在已有路径v1-->v2-->v3……-->vk
新加一个点v_k+1,考虑vk与v_k+1之间边的方向
A、若vk-->v_k+1,那直接把v_k+1加在vk后面即可
B、若v_k+1-->vk,从vk往前枚举 vi,找到第一个存在边vi-->vk的vi,
vi之后的点vj(j>i)都存在边v_k+1-->vj,所以把v_k+1插在vi后面即可
如果找不到这样的vi,说明对于所有的vi,存在边v_k+1-->vi
把v_k+1放到最前面即可
六、求竞赛图的哈密顿通路代码
输入一张竞赛图,
格式为n*n的01矩阵
第i行第j列为1表示存在边i-->j

#include<cstdio> #include<cstring> #include<iostream> using namespace std; #define N 2001 int n; char s[N<<1]; int e[N][N]; int front,nxt[N]; int st[N]; void Hamilton() { front=1; memset(nxt,0,sizeof(nxt)); for(int i=2;i<=n;++i) { if(e[front][i]) { nxt[i]=front; front=i; continue; } int j,k; for(j=front;j;k=j,j=nxt[j]) if(e[j][i]) { nxt[i]=j; nxt[k]=i; break; } if(!j) nxt[k]=i; } } void print() { int now=front; int top=0; while(now) { st[++top]=now; now=nxt[now]; } for(int i=top;i>1;--i) printf("%d ",st[i]); printf("%d\\n",st[1]); } int main() { while(scanf("%d",&n)!=EOF) { memset(e,false,sizeof(e)); for(int i=1;i<=n;++i) { getchar(); scanf("%[^\\n]",s); int t=0; for(int j=0;t<n;j+=2) e[i][++t]=s[j]-\'0\'; } Hamilton(); print(); } }
七、竞赛图上的哈密顿回路
定理:竞赛图的任意强连通子图必存在哈密顿回路
法一、枚举起点,求哈密顿通路,判断是否首尾相连
法二、在哈密顿通路的基础上构造回路
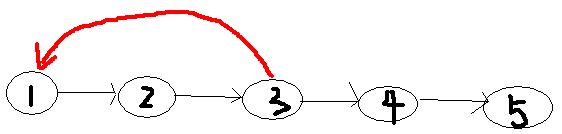
假设现在有这样的一条哈密顿通路

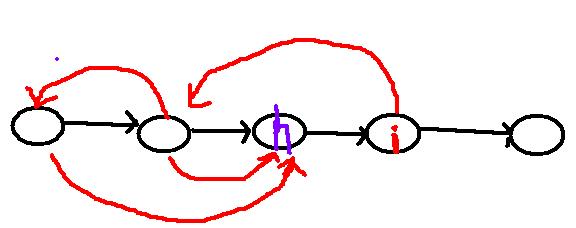
1、找到第一个能连回1号点的点,下图中为3号点,设其为L,1号点为R
得到了一个环,现在扩充这个环,使其包含所有节点
2、从L往后枚举每个点i,表示现在要把点i加入环中
从R开始枚举已求出的环上的每个点,找到第一个存在边i-->j 的点j
如果找不到这样的点j,继续枚举i的下一个点
下图中i为4号点,j为2号点,那么j之前枚举到的环上的点k一定存在边k-->i
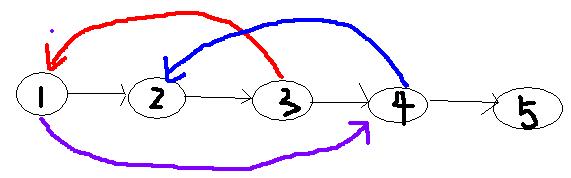
就得到了1条新的哈密顿回路
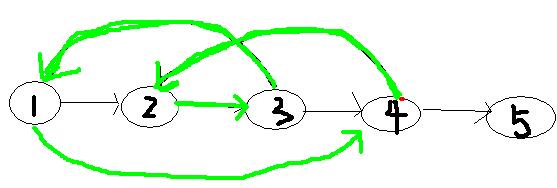
比较它与原来的哈密顿回路
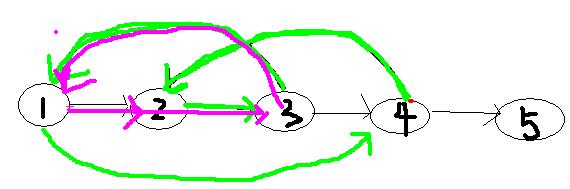
除了新加入的点之外,只有点j的上一个点的出边改变,指向新加入的点
所以记录j的上一个点k,这里k=1
把新的点i插到k后面即可
如果点i之前存在跳过去的点,那么需要把这些点一起插入k的后面
下图中点h是被跳过去的点
代码:
已有一条从l开始的哈密顿通路
r=0; for(int i=nxt[l];i;i=nxt[i]) if(r) { for(int j=r,k=l;;k=j,j=nxt[j]) { if(mp[i][j]) { nxt[k]=nxt[l]; if(k!=l) nxt[l]=r; l=i; r=j; break; } if(j==l) break; } } else if(mp[i][l]) r=l,l=i; nxt[l]=r;
以上是关于哈密顿图的判定的主要内容,如果未能解决你的问题,请参考以下文章
