概率论高速学习04:概率公理 全概率 贝叶斯 事件独立性
Posted llguanli
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了概率论高速学习04:概率公理 全概率 贝叶斯 事件独立性相关的知识,希望对你有一定的参考价值。
概率论高速学习04:概率公理 全概率 贝叶斯 事件独立性
原创地址: http://www.cnblogs.com/Alandre/ (泥沙砖瓦浆木匠),须要转载的,保留下! Thanks
加油! 大牛总是不断努力,你却更须要加倍努力.
Written In The Font
数学和生活是技术之本, 有了数学,加上生活,才会开心.
今天继续概率论:
- 全概率
- 贝叶斯
- 事件独立性
Content
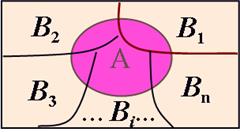
The total probability
The law of total probability is the proposition that if 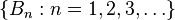 is
a finite or countably infinitepartition of a sample space (in other words, a set of pairwise disjoint events whose union is the entire sample space) and each event
is
a finite or countably infinitepartition of a sample space (in other words, a set of pairwise disjoint events whose union is the entire sample space) and each event  is measurable,
then for any event
is measurable,
then for any event  of the same probability space:
of the same probability space:

example:
例. 甲、乙两家工厂生产某型号车床,当中次品率分别为20%, 5%。已知每月甲厂生产的数量是乙厂的两倍,现从一个月的产品中随意抽检一件,求该件产品为合格的概率?
设A表示产品合格,B表示产品来自甲厂
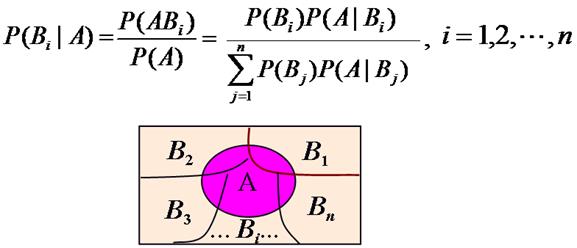
Bayes
for some partition {Bj} of the event space, the event space is given or conceptualized in terms of P(Bj) and P(A|Bj). It is then useful to compute P(A) using the law of total probability:
example:
An entomologist spots what might be a rare subspecies of beetle, due to the pattern on its back. In the rare subspecies, 98% have the pattern, or P(Pattern|Rare) = 98%. In the common subspecies, 5% have the pattern. The rare subspecies accounts for only 0.1% of the population. How likely is the beetle having the pattern to be rare, or what is P(Rare|Pattern)?
From the extended form of Bayes\' theorem (since any beetle can be only rare or common),
![\\begin{align}P(\\text{Rare}|\\text{Pattern}) &=\\frac{P(\\text{Pattern}|\\text{Rare})P(\\text{Rare})} {P(\\text{Pattern}|\\text{Rare})P(\\text{Rare}) \\, + \\, P(\\text{Pattern}|\\text{Common})P(\\text{Common})} \\\\[8pt]&= \\frac{0.98 \\times 0.001} {0.98 \\times 0.001 + 0.05 \\times 0.999} \\\\[8pt]&\\approx 1.9\\%. \\end{align}](http://upload.wikimedia.org/math/e/c/9/ec9fbb7a49f0f0bffac7f49fba84d7c0.png)
One more example:
Independence
Two events
Two events A and B are independent if and only if their joint probability equals the product of their probabilities:
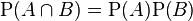 .
.
Why this defines independence is made clear by rewriting with conditional probabilities:
how about Three events
sometimes , we will see the Opposition that can be used to make the mess done. We will use the rule of independence such as : 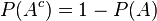
Editor\'s Note
“学吧,至少不亏.”一句良言 终身受用.
以上是关于概率论高速学习04:概率公理 全概率 贝叶斯 事件独立性的主要内容,如果未能解决你的问题,请参考以下文章
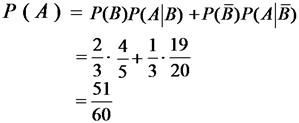

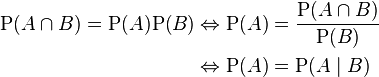
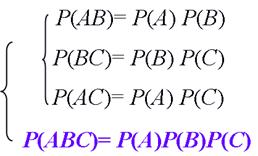

 好友:
好友: