算法分析初步

Posted 2020-10-23 一束没有希望的光

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了算法分析初步相关的知识，希望对你有一定的参考价值。

注：这个是我去年这个时候做的笔记，现在这部分内容我已经基本掌握，在博客上做个备份

算法分析

一、渐进符号

渐近分析是一种描述函数在极限附近的行为的方法，算法分析一般考虑给定算法在输入非常大的数据集时候的性能。

定义1.1：\$O\$记号

\$f(n)=O(g(n)):\$表示存在正常量\$c\$和\$n_0\$，使得对所有的\$n\\ge n_0\$，有\$0\\le f(n)\\le cg(n)\$。

这个符号用来表示函数的渐进上界，比如\$2n^2=O(n^3)\$。

这其中的等号不是对称的，因为\$O\$记号定义了一个函数集：

\$O(g(n))=\\{f(n):\\text{存在正常量和\$n_0\$，使得对所有的\$n\\ge n_0，0\\le f(n)\\le cg(n)\$}\\}\$。

所以不能够理解为\$2n^2\$等于\$O(n^3)\$，而只能理解为\$2n^2\$属于函数集\$O(n^3)\$

这个符号还可以用来描述误差界限，如：\$f(n)=n^3+O(n^2)\$，表示这个函数主要是\$n^3\$，还有一些至多\$O(n^2)\$的项。

类似地我们可以定义一个函数的渐进下界：

定义1.2：\$\\Omega\$记号

\$f(n)=\\Omega(g(n)):\$ 表示存在正常量\$c\$和\$n_0\$，使得对所有的\$n\\ge n_0\$，有\$0\\le cg(n)\\le f(n)\$。

\$\\Omega(g(n))=\\{f(n):\\text{存在正常量\$c\$和\$n_0\$，使得对所有的\$n\\ge n_0，有0\\le cg(n)\\le f(n)\$}\\}\$

如：\$\\sqrt{n}=\\Omega(\\log n)\$。

接下来我们定义渐进紧确界：

定义1.3：\$\\Theta\$记号

\$\\Theta(g(n))=\\{f(n): \\text{存在正常量\$c_1\$,\$c_2\$和\$n_0\$，使得对所有的\$n\\ge n_0，有0\\le c_1g(n)\\le f(n)\\le c_2g(n)\$}\\}\$

如：\$2n^2=\\Theta(n^2)\$

显然对任意两个函数\$f(n)\$和\$g(n)\$，我们有\$f(n)=\\Theta(g(n))\$，当且仅当\$f(n)=O(g(n))\$且\$f(n)=\\Omega(g(n))\$

由\$O\$定义的渐进上界可能是也可能不是渐进紧确的,用类似\$ε-δ\$语言的方法，我们可以定义一个非渐进紧确的上界。

定义1.4：\$o\$记号

\$o(g(n))=\\{f(n):\\text{对任意常量\$c>0\$，存在常量\$n_0>0\$，使得对所有的\$n\\ge n_0，有0\\le f(n)\\le cg(n)\$\\}}\$

如：\$n^2=o(n^3)(n_0=\\frac{2}{c})\$。

有些学者还喜欢用$$\\lim_{n\\to\\infty} \\frac{f(n)}{g(n)}=0$$来定义\$o\$符号，带入函数极限的定义，对任给正数\$n\$，总存在\$n_0\$，使得当\$n>n_0\$时有\$\\left|\\frac{f(n)}{g(n)}-0\\right|<c\$，整理即得\$f(n)<cg(n)\$

同样地我们定义\$\\Omega\$记号

定义1.5：\$\\Omega\$记号

\$\\Omega(g(n))=\\{f(n):\\text{对任意常量\$c>0\$，存在常量\$n_0>0\$，使得对所有的\$n\\ge n_0$，有\$0\\le cg(n)\\le f(n)\$}}$

以及$$\\lim_{n\\to\\infty}\\frac{f(n)}{g(n)}=+\\infty$$

性质

传递性：\$5\$个符号都具有传递性，\$f(n)=O(g(n))\$且\$g(n)=O(h(n)) \\to f(n)=O(h(n))\$
自反性：\$\\Omega,\\Theta,O\$记号具有自反性，\$f(n)=O(f(n))\$
对称性：\$\\Theta\$具有对称性，\$f(n)=\\Theta(g(n))\$,当且仅当\$g(n)=\\Theta(f(n))\$
转置对称性：\$f(n)=O(g(n))\$当且仅当\$g(n)=\\Omega(f(n))\$,\$f(n)=o(g(n))\$当且仅当\$g(n)=\\Omega(f(n))\$

二、递归式的求解

我们经常使用递归方法来解决问题，因此会出现一些递归式，对于递归式时间复杂度的求解，并没有通用的方法,主要有以下几种方法

1.代入法，先猜后证

先猜出一个结果，再使用数学归纳法进行证明

注意，在进行数学归纳法的推导时，不要使用\$O\$记号进行推导，很容易产生悖论

比如，我们可以证明\$n=O(1)\$,进而所有的算法都是\$O(1)\$的

归纳奠基：\$1=O(1)\$

归纳假设：假设\$k=O(1)\$

归纳递推：\$k+1=O(1)+O(1)=O(1)\$

所以对所有的自然数\$n\$均成立，\$n=O(1)\$

错误在于，在向下递推\$O(1)\$的过程中，\$O(1)\$会依赖于\$n\$变化

解：\$T(n)=4T(n/2)+n,T(1)=\\Theta(1)\$

首先猜想它是\$O(n^2)\$的，使用第二数学归纳法，假设存在$c_1,c_2,s.t. \$当\$k<n\$时，\$T(k)\\le c_1k^2-c_2k$

\$T(n)\\le 4\\left(c_1\\left(\\frac{n}{2}\\right)^2-c_2\\frac{n}{2}+\\frac{n}{2}\\right)+n=c_1n^2-c_2n-(c_2-1)n\\le c_1n^2-c_2n\$，当\$c_2\\ge 1\$时

\$c_1\$也有相应的范围，考虑到\$T(1)=c_1-c_2>0,c_1>c_2\$

同理我们还可以证明这个递推式是\$\\Omega(n^2)\$的，进而推出这个递推式是\$\\Theta(n^2)的\$

2.递归树方法

画出递归树，对递归树的每一层进行求和，然后将所有的层求和

如对于\$T(n)=3T\\left( \\left \\lfloor \\frac{n}{4} \\right\\rfloor\\right)+\\Theta(n^2)\$，画出的递归树如下

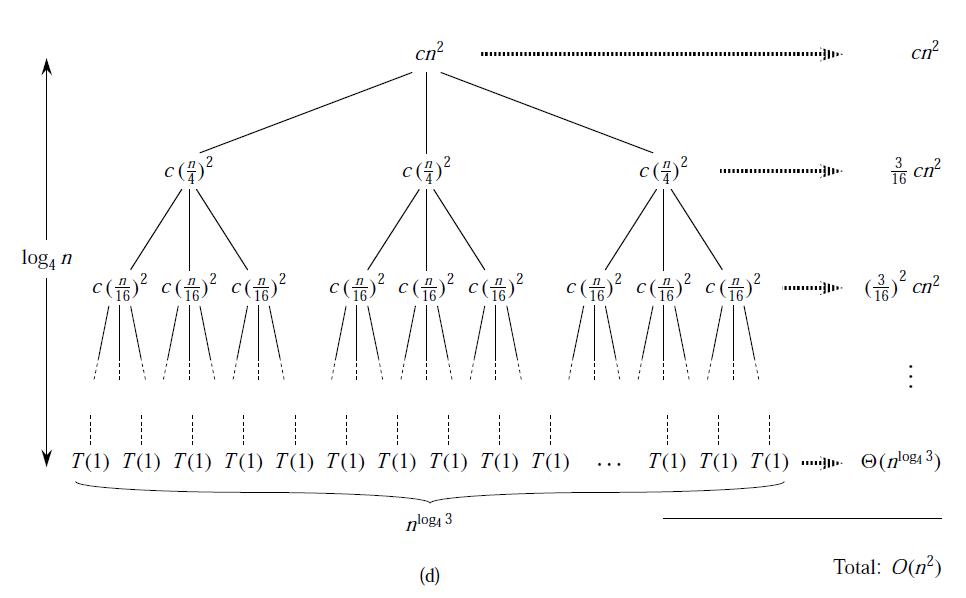
对表达式进行求和，可得$$T(n)=\\sum_{1}^{{\\log_4n}{\\left(\\frac{3}{16}\\right)}icn^2}+\\Theta(n{\\log_43})<\\sum_{1}^{{\\infty}{\\left(\\frac{3}{16}\\right)}icn^{2}+\\Theta\\left(n}{\\log_43}\\right)=\\frac{16}{13}cn^{2+\\Theta\\left(n}{\\log_43}\\right)=O(n^2)$$

因为表达式中有\$\\Theta(n^2)\$，所以\$T(n)\$显然是\$\\Omega(n^2)\$的，所以\$T(n)\$是\$\\Theta(n^2)\$的

很多时候我们不必求出准确值，而只需进行恰当的放缩，如\$T(n)=T\\left(\\frac{n}{3}\\right)+T\\left(\\frac{2n}{3}\\right)+cn\$,显然两侧下降的不一样快，左子树会先到达叶子节点，但我们使用\$\\log_{\\frac{3}{2}}n\$作为树高和计算叶子节点的数量，不会改变\$O\$的数量级

3.主方法

套现成的公式

主定理：令\$a\\ge 1\$和\$b>1\$是常数，\$f(n)\$是一个函数，\$T(n)\$是定义在非负整数上的递归式\$T(n)=aT(\\frac{n}{b})+f(n)\$

那么\$T(n)\$有如下渐进界：

\$1\$.若对于某个常数\$ε>0\$有\$f(n)=O\\left(n^{\\log_ba-ε}\\right)\$，则\$T(n)=\\Theta\\left(n^{\\log_ba}\\right)\$

\$2\$.若对于某个常数\$k\\ge 0\$有\$f(n)=\\Theta\\left(n^{\\log_ba}\\log^kn\\right)\$，则\$T(n)=\\Theta\\left(n^{\\log_ba}\\log^{k+1}n\\right)\$

\$3\$.若对某个常数\$ε>0\$有\$f(n)=\\Omega\\left(n^{\\log_ba+ε}\\right)\$，且对某个常数\$c<1\$和所有足够大的\$n\$有\$af\\left(\\frac{n}{b}\\right)\\le cf(n)\$，则\$T(n)=\\Theta(f(n))\$

4.Akra-Bazzi方法

\\[T(x)=\\left\\{ \\begin{aligned} \\Theta(1)\\qquad若1\\le x \\le x_0 \\\\ \\sum_{i=1}^k{a_iT(b_ix)}+f(x)\\qquad若x>x_0 \\\\ \\end{aligned} \\right. \\]

则递归式的解为

\\[T(n)=\\Theta\\left(x^p\\left(1+\\int_1^x\\frac{f(u)}{u^{p+1}}du\\right)\\right) \\]

证明均见《算法导论》

三、常用算法的时间复杂度

搜索

算法	数据结构	时间复杂度（平均）	时间复杂度（最差）	空间复杂度（最差）
深度优先搜索（DFS）	\$\\left\\\|V\\right\\\|\$个点\$\\left\\\|E\\right\\\|\$个边的图	-	\$O(\\left\\\|E\\right\\\|+\\left\\\|V\\right\\\|)\$	\$O(\\left\\\|V\\right\\\|)\$
广度优先搜索（BFS）	\$\\left\\\|V\\right\\\|\$个点\$\\left\\\|E\\right\\\|\$个边的图	-	\$O(\\left\\\|E\\right\\\|+\\left\\\|V\\right\\\|)\$	\$O(\\left\\\|V\\right\\\|)\$
二分查找	排好序的数组	\$\\Theta(\\log n)\$	\$O(\\log n)\$	\$O(1)\$
穷举查找	数组	\$\\Theta(n)\$	\$O(n)\$	\$O(1)\$
Dijkstra算法（小根堆）	\$\\left\\\|V\\right\\\|\$个点\$\\left\\\|E\\right\\\|\$个边的图	\$\\Theta((\\left\\\|V\\right\\\|+\\left\\\|E\\right\\\|)\\log\\left\\\|V\\right\\\|)\$	\$O((\\left\\\|V\\right\\\|+\\left\\\|E\\right\\\|)\\log\\left\\\|V\\right\\\|)\$	\$O(\\left\\\|V\\right\\\|)\$
Dijkstra算法（无序数组）	\$\\left\\\|V\\right\\\|\$个点\$\\left\\\|E\\right\\\|\$个边的图	$ \\Theta(\\left\|V\\right\|^2)$	\$O(\\left\\\|V\\right\\\|^2)\$	\$O(\\left\\\|V\\right\\\|)\$
Bellman-Ford算法	\$\\left\\\|V\\right\\\|\$个点\$\\left\\\|E\\right\\\|\$个边的图	\$\\Theta(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\$	\$O(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\$	\$O(\\left\\\|V\\right\\\|)\$
Floyd-Warshell算法	\$\\left\\\|V\\right\\\|\$个点\$\\left\\\|E\\right\\\|\$个边的图	\$\\Theta(\\left\\\|V\\right\\\|^3)\$	\$O(\\left\\\|V\\right\\\|^3)\$	\$O(\\left\\\|V\\right\\\|^2)\$

排序

算法	数据结构	时间复杂度（最佳）	时间复杂度（平均）	时间复杂度（最差）	辅助空间复杂度（最差）
快速排序	数组	\$\\Omega(n\\log n)\$	\$\\Theta(n\\log n)\$	\$O(n^2)\$	\$O(n)\$
归并排序	数组	\$\\Omega(n\\log n)\$	\$\\Theta(n\\log n)\$	\$O(n\\log n)\$	\$O(n)\$
堆排序	数组	\$\\Omega(n\\log n)\$	\$\\Theta(n\\log n)\$	\$O(n\\log n)\$	\$O(1)\$
冒泡排序	数组	\$\\Omega(n)\$	\$\\Theta(n^2)\$	\$O(n^2)\$	\$O(1)\$
插入排序	数组	\$\\Omega(n)\$	\$\\Theta(n^2)\$	\$O(n^2)\$	\$O(1)\$
选择排序	数组	\$\\Omega(n^2)\$	\$\\Theta(n^2)\$	\$O(n^2)\$	\$O(1)\$
桶排序	数组	\$\\Omega(n+k)\$	\$\\Theta(n+k)\$	\$O(n^2)\$	\$O(nk)\$
基数排序	数组	\$\\Omega(nk)\$	\$\\Theta(nk)\$	\$O(nk)\$	\$O(n+k)\$

数据结构

数据结构	时间复杂度（平均）				时间复杂度（最差）			空间复杂度（最差）
操作	索引	查找	插入	删除	索引	查找	插入\\删除
基本数组	\$\\Theta(1)\$	\$\\Theta(n)\$	\$-\$	\$-\$	\$O(1)\$	\$O(n)\$	\$-\$	\$O(n)\$
动态数组	\$\\Theta(1)\$	\$\\Theta(n)\$	\$\\Theta(n)\$	\$\\Theta(n)\$	\$O(1)\$	\$O(n)\$	\$O(n)\$	\$O(n)\$
单链表	\$\\Theta(n)\$	\$\\Theta(n)\$	\$\\Theta(1)\$	\$\\Theta(1)\$	\$O(n)\$	\$O(n)\$	\$O(1)\$	\$O(n)\$
双链表	\$\\Theta(n)\$	\$\\Theta(n)\$	\$\\Theta(1)\$	\$\\Theta(1)\$	\$O(n)\$	\$O(n)\$	\$O(1)\$	\$O(n)\$
跳表	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$O(n)\$	\$O(n)\$	\$O(n)\$	\$O(n\\log n)\$
哈希表	\$-\$	\$\\Theta(1)\$	\$\\Theta(1)\$	\$\\Theta(1)\$	\$-\$	\$O(n)\$	\$O(n)\$	\$O(n)\$
二叉搜索树	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$\\Theta(n)\$	\$O(n)\$	\$O(n)\$	\$O(n)\$	\$O(n)\$
笛卡尔树	\$-\$	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$-\$	\$O(n)\$	\$O(n)\$	\$O(n)\$	\$O(n)\$
B-树	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(n)\$
红黑树	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(n)\$
伸展树	\$-\$	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$-\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(n)\$
AVL树	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$\\Theta(\\log n)\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(n)\$

堆

种类	时间复杂度
操作	建堆	查找最大值	提取最大值	维护	插入	删除	合并
链表（已排序）	\$-\$	\$O(1)\$	\$O(1)\$	\$O(n)\$	\$O(n)\$	\$O(1)\$	\$O(m+n)\$
链表（未排序）	\$-\$	\$O(n)\$	\$O(n)\$	\$O(1)\$	\$O(1)\$	\$O(1)\$	\$O(1)\$
二叉堆	\$O(n)\$	\$O(1)\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(m+n)\$
二项堆	\$-\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(\\log n)\$	\$O(\\log n)\$
斐波那契堆	\$-\$	\$O(1)\$	\$O(\\log n)\$	\$O(1)\$	\$O(1)\$	\$O(\\log n)\$	\$O(1)\$

图

管理	存储	加点	加边	去点	去边	查询
邻接表	\$O(\\left\\\|V\\right\\\|+\\left\\\|E\\right\\\|)\$	\$O(1)\$	\$O(1)\$	\$O(\\left\\\|V\\right\\\|+\\left\\\|E\\right\\\|)\$	\$O(\\left\\\|E\\right\\\|)\$	\$O(\\left\\\|V\\right\\\|)\$
关联表	\$O(\\left\\\|V\\right\\\|+\\left\\\|E\\right\\\|)\$	\$O(1)\$	\$O(1)\$	\$O(\\left\\\|E\\right\\\|)\$	\$O(\\left\\\|E\\right\\\|)\$	\$O(\\left\\\|E\\right\\\|)\$
邻接矩阵	\$O(\\left\\\|V\\right\\\|^2)\$	\$O(\\left\\\|V\\right\\\|^2)\$	\$O(1)\$	\$O(\\left\\\|V\\right\\\|^2)\$	\$O(\\left\\\|V\\right\\\|^2)\$	\$O(1)\$
关联矩阵	\$O(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\$	\$O(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\$	\$O(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\$	\$O(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\$	\$O(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\$	\$O(\\left\\\|E\\right\\\|)\$

以上是关于算法分析初步的主要内容，如果未能解决你的问题，请参考以下文章

高级数据分析可视化低代码技术框架选型初步分析

《入门经典》——6.29

Paxos分析

机器学习Sklearn的k近邻算法api初步使用

超多分析结果表简单字段关联生成大宽表的初步猜想

算法	数据结构	时间复杂度（平均）	时间复杂度（最差）	空间复杂度（最差）
深度优先搜索（DFS）	\\(\\left\\\|V\\right\\\|\\)个点\\(\\left\\\|E\\right\\\|\\)个边的图	-	\\(O(\\left\\\|E\\right\\\|+\\left\\\|V\\right\\\|)\\)	\\(O(\\left\\\|V\\right\\\|)\\)
广度优先搜索（BFS）	\\(\\left\\\|V\\right\\\|\\)个点\\(\\left\\\|E\\right\\\|\\)个边的图	-	\\(O(\\left\\\|E\\right\\\|+\\left\\\|V\\right\\\|)\\)	\\(O(\\left\\\|V\\right\\\|)\\)
二分查找	排好序的数组	\\(\\Theta(\\log n)\\)	\\(O(\\log n)\\)	\\(O(1)\\)
穷举查找	数组	\\(\\Theta(n)\\)	\\(O(n)\\)	\\(O(1)\\)
Dijkstra算法（小根堆）	\\(\\left\\\|V\\right\\\|\\)个点\\(\\left\\\|E\\right\\\|\\)个边的图	\\(\\Theta((\\left\\\|V\\right\\\|+\\left\\\|E\\right\\\|)\\log\\left\\\|V\\right\\\|)\\)	\\(O((\\left\\\|V\\right\\\|+\\left\\\|E\\right\\\|)\\log\\left\\\|V\\right\\\|)\\)	\\(O(\\left\\\|V\\right\\\|)\\)
Dijkstra算法（无序数组）	\\(\\left\\\|V\\right\\\|\\)个点\\(\\left\\\|E\\right\\\|\\)个边的图	$ \\Theta(\\left\|V\\right\|^2)$	\\(O(\\left\\\|V\\right\\\|^2)\\)	\\(O(\\left\\\|V\\right\\\|)\\)
Bellman-Ford算法	\\(\\left\\\|V\\right\\\|\\)个点\\(\\left\\\|E\\right\\\|\\)个边的图	\\(\\Theta(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\\)	\\(O(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\\)	\\(O(\\left\\\|V\\right\\\|)\\)
Floyd-Warshell算法	\\(\\left\\\|V\\right\\\|\\)个点\\(\\left\\\|E\\right\\\|\\)个边的图	\\(\\Theta(\\left\\\|V\\right\\\|^3)\\)	\\(O(\\left\\\|V\\right\\\|^3)\\)	\\(O(\\left\\\|V\\right\\\|^2)\\)

算法	数据结构	时间复杂度（最佳）	时间复杂度（平均）	时间复杂度（最差）	辅助空间复杂度（最差）
快速排序	数组	\\(\\Omega(n\\log n)\\)	\\(\\Theta(n\\log n)\\)	\\(O(n^2)\\)	\\(O(n)\\)
归并排序	数组	\\(\\Omega(n\\log n)\\)	\\(\\Theta(n\\log n)\\)	\\(O(n\\log n)\\)	\\(O(n)\\)
堆排序	数组	\\(\\Omega(n\\log n)\\)	\\(\\Theta(n\\log n)\\)	\\(O(n\\log n)\\)	\\(O(1)\\)
冒泡排序	数组	\\(\\Omega(n)\\)	\\(\\Theta(n^2)\\)	\\(O(n^2)\\)	\\(O(1)\\)
插入排序	数组	\\(\\Omega(n)\\)	\\(\\Theta(n^2)\\)	\\(O(n^2)\\)	\\(O(1)\\)
选择排序	数组	\\(\\Omega(n^2)\\)	\\(\\Theta(n^2)\\)	\\(O(n^2)\\)	\\(O(1)\\)
桶排序	数组	\\(\\Omega(n+k)\\)	\\(\\Theta(n+k)\\)	\\(O(n^2)\\)	\\(O(nk)\\)
基数排序	数组	\\(\\Omega(nk)\\)	\\(\\Theta(nk)\\)	\\(O(nk)\\)	\\(O(n+k)\\)

数据结构	时间复杂度（平均）				时间复杂度（最差）			空间复杂度（最差）
操作	索引	查找	插入	删除	索引	查找	插入\\删除
基本数组	\\(\\Theta(1)\\)	\\(\\Theta(n)\\)	\\(-\\)	\\(-\\)	\\(O(1)\\)	\\(O(n)\\)	\\(-\\)	\\(O(n)\\)
动态数组	\\(\\Theta(1)\\)	\\(\\Theta(n)\\)	\\(\\Theta(n)\\)	\\(\\Theta(n)\\)	\\(O(1)\\)	\\(O(n)\\)	\\(O(n)\\)	\\(O(n)\\)
单链表	\\(\\Theta(n)\\)	\\(\\Theta(n)\\)	\\(\\Theta(1)\\)	\\(\\Theta(1)\\)	\\(O(n)\\)	\\(O(n)\\)	\\(O(1)\\)	\\(O(n)\\)
双链表	\\(\\Theta(n)\\)	\\(\\Theta(n)\\)	\\(\\Theta(1)\\)	\\(\\Theta(1)\\)	\\(O(n)\\)	\\(O(n)\\)	\\(O(1)\\)	\\(O(n)\\)
跳表	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(O(n)\\)	\\(O(n)\\)	\\(O(n)\\)	\\(O(n\\log n)\\)
哈希表	\\(-\\)	\\(\\Theta(1)\\)	\\(\\Theta(1)\\)	\\(\\Theta(1)\\)	\\(-\\)	\\(O(n)\\)	\\(O(n)\\)	\\(O(n)\\)
二叉搜索树	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(\\Theta(n)\\)	\\(O(n)\\)	\\(O(n)\\)	\\(O(n)\\)	\\(O(n)\\)
笛卡尔树	\\(-\\)	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(-\\)	\\(O(n)\\)	\\(O(n)\\)	\\(O(n)\\)	\\(O(n)\\)
B-树	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(n)\\)
红黑树	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(n)\\)
伸展树	\\(-\\)	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(-\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(n)\\)
AVL树	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(\\Theta(\\log n)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(n)\\)

种类	时间复杂度
操作	建堆	查找最大值	提取最大值	维护	插入	删除	合并
链表（已排序）	\\(-\\)	\\(O(1)\\)	\\(O(1)\\)	\\(O(n)\\)	\\(O(n)\\)	\\(O(1)\\)	\\(O(m+n)\\)
链表（未排序）	\\(-\\)	\\(O(n)\\)	\\(O(n)\\)	\\(O(1)\\)	\\(O(1)\\)	\\(O(1)\\)	\\(O(1)\\)
二叉堆	\\(O(n)\\)	\\(O(1)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(m+n)\\)
二项堆	\\(-\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)	\\(O(\\log n)\\)
斐波那契堆	\\(-\\)	\\(O(1)\\)	\\(O(\\log n)\\)	\\(O(1)\\)	\\(O(1)\\)	\\(O(\\log n)\\)	\\(O(1)\\)

管理	存储	加点	加边	去点	去边	查询
邻接表	\\(O(\\left\\\|V\\right\\\|+\\left\\\|E\\right\\\|)\\)	\\(O(1)\\)	\\(O(1)\\)	\\(O(\\left\\\|V\\right\\\|+\\left\\\|E\\right\\\|)\\)	\\(O(\\left\\\|E\\right\\\|)\\)	\\(O(\\left\\\|V\\right\\\|)\\)
关联表	\\(O(\\left\\\|V\\right\\\|+\\left\\\|E\\right\\\|)\\)	\\(O(1)\\)	\\(O(1)\\)	\\(O(\\left\\\|E\\right\\\|)\\)	\\(O(\\left\\\|E\\right\\\|)\\)	\\(O(\\left\\\|E\\right\\\|)\\)
邻接矩阵	\\(O(\\left\\\|V\\right\\\|^2)\\)	\\(O(\\left\\\|V\\right\\\|^2)\\)	\\(O(1)\\)	\\(O(\\left\\\|V\\right\\\|^2)\\)	\\(O(\\left\\\|V\\right\\\|^2)\\)	\\(O(1)\\)
关联矩阵	\\(O(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\\)	\\(O(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\\)	\\(O(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\\)	\\(O(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\\)	\\(O(\\left\\\|V\\right\\\|\\left\\\|E\\right\\\|)\\)	\\(O(\\left\\\|E\\right\\\|)\\)

算法分析初步

算法分析

一、渐进符号

定义1.1：\\(O\\)记号

定义1.2：\\(\\Omega\\)记号

定义1.3：\\(\\Theta\\)记号

定义1.4：\\(o\\)记号

定义1.5：\\(\\Omega\\)记号

性质