图论——最小生成树①

Posted 2020-10-23 aidenpearce

RT

题目描述

国防部计划用无线网络连接若干个边防哨所。2 种不同的通讯技术用来搭建无线网络；

每个边防哨所都要配备无线电收发器；有一些哨所还可以增配卫星电话。

任意两个配备了一条卫星电话线路的哨所（两边都?有卫星电话）均可以通话，无论

他们相距多远。而只通过无线电收发器通话的哨所之间的距离不能超过 D，这是受收发器

的功率限制。收发器的功率越高，通话距离 D 会更远，但同时价格也会更贵。

收发器需要统一购买和安装，所以全部哨所只能选择安装一种型号的收发器。换句话

说，每一对哨所之间的通话距离都是同一个 D。你的任务是确定收发器必须的最小通话距

离 D，使得每一对哨所之间至少有一条通话路径（直接的或者间接的）。

输入输出格式

输入格式：

输入数据第 1 行，2 个整数 S 和 P，S 表示可安装的卫星电话的哨所

数，P 表示边防哨所的数量。接下里 P 行，每行两个整数 x，y 描述一个哨所的平面坐标

(x, y)，以 km 为单位。

输出格式：

第 1 行，1 个实数 D，表示无线电收发器的最小传输距离，?确到小数点后两位。

输入输出样例

输入样例#1： 

2 4
0 100
0 300
0 600
150 750

输出样例#1：

212.13

刚开始没读懂题，后来才直到，大概就是说有一些卫星设备，可以无花费的连边，就是有卫星设备的点之间，边的权值就是0；
好像就会了，一个最小生成树；
然后就有坑了
错误的思路：
每两个设备去掉一个边，s个设备去s/2个边，然后贪心删去；（呵呵）
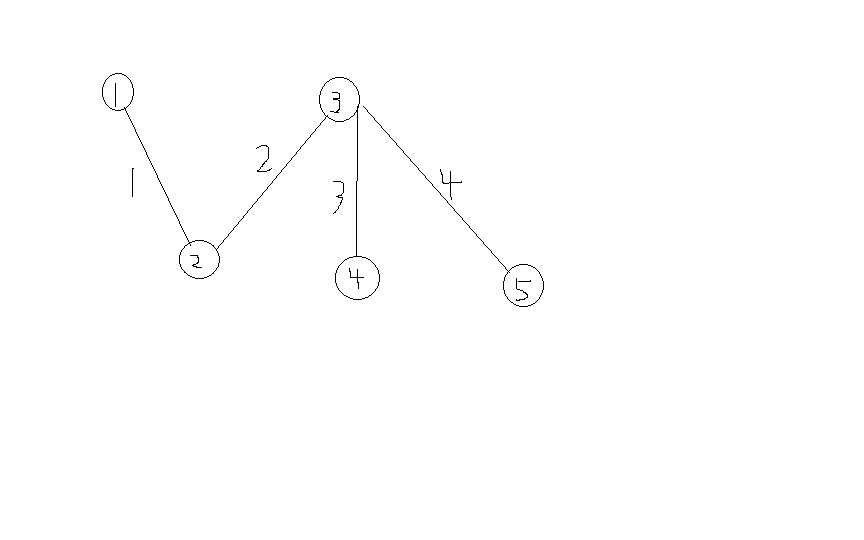
就像下图，假如有3个设备；
其实，你只要在5,3,4放就行
如果总的来说，就是你从两个设备开始，你每多加一个，你就能去一个边。OJBK.
用prim，求出最小生成树的所有边长，然后找出第q-s大的；

#include <cstdio>
#include <algorithm>
#include <queue>
#include <cmath>

using namespace std;
struct data{int v,nxt;double val;}edge[260000];
int cnt,alist[600];
inline void add(int u,int v,double val)
{
    edge[++cnt].v=v;edge[cnt].val=val;
    edge[cnt].nxt=alist[u];alist[u]=cnt;
}
struct nod
{
    int num;double val;
    friend bool operator <(nod a,nod b){return a.val>b.val;}
};
double juli(double x1,double y1,double x2,double y2)
{
    double lon;
    lon=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
    return lon;
}
double res[360000];
priority_queue <nod> pq;
int tim;
bool vis[600];double d[600];
int s,p;double x[600],y[600];
bool cmp(double a,double b)
{return a<b;
}
int main()
{
    scanf("%d%d",&s,&p);
    for(int i=1;i<=p;++i)
    {
        scanf("%lf %lf",&x[i],&y[i]);
    }
    for(int i=1;i<=p;++i)
    {
        for(int j=1;j<=p;++j)
        {
            if(i==j) continue;
            add(i,j,juli(x[i],y[i],x[j],y[j]));
        }
    }
    for(int i=1;i<=p;++i){d[i]=0x3f3f3f3f;}
    nod poi;poi.num=1;d[1]=0;poi.val=0;pq.push(poi);
    while(!pq.empty())
    {
        nod now=pq.top();pq.pop();if(vis[now.num])continue;
        vis[now.num]=true;res[++tim]=now.val;
        int nxt=alist[now.num];
        while(nxt)
        {
            int v=edge[nxt].v;
            double val=edge[nxt].val;
            if(d[v]>val&&vis[v]==false)
            {
                d[v]=val;nod poi;
                poi.num=v;poi.val=val;
                pq.push(poi);
            }
            nxt=edge[nxt].nxt;
        }
    }
        sort(res+1,res+1+p,cmp);
        printf("%0.2lf\\n",res[p-s+1]);
}

View Code

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2018-02-07 16:39:53