k-近邻算法（K-Nearest Neighbor）

Posted 2020-10-23 rockrunner

一、概述

　　k-近邻算法采用测量不同特征值之间的距离方法进行分类

1、工作原理：

　　存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。最后，选择k个最相似数据中出现次数最多的分类，作为新数据的分类。

　　通常k取不大于20的整数，一般为了方便利用少数服从多数的投票法则(Majority-voting)，k取质数。

2、举例分析：电影分类

　　首先我们从动作片和爱情片中提取出两个特征--打斗和接吻。并对已知类型的6部电影和未知类型电影的两个特征进行统计如下：

 

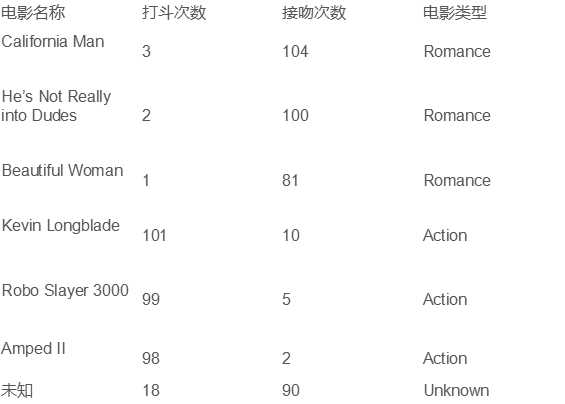
图 1 打斗与接吻特征统计

　　这样我们可以将7部电影抽象为二维坐标系中的7个点，将两个特征分别抽象为对应点的X坐标值和Y坐标值，如下图：

 

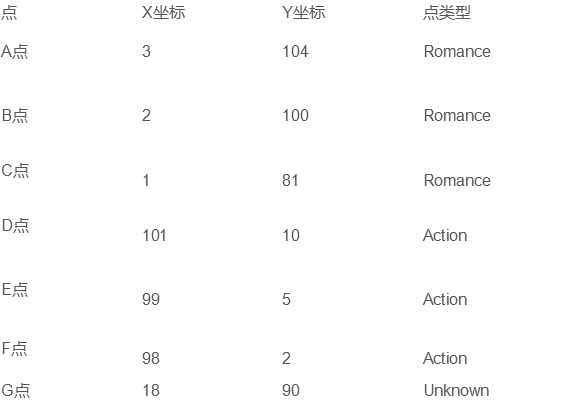
图 2：抽象后的特征数据

然后就可以根据抽象得到的数据用散点图来表示：

 

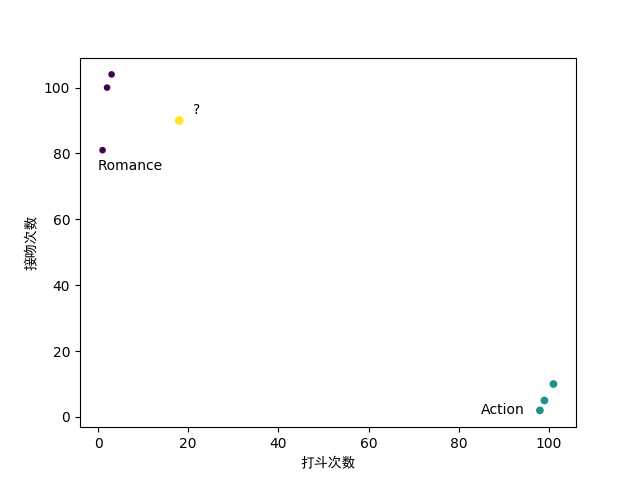
图 3：电影分类散点图

　　这时我们需要计算不同特征值之间的距离，即图3 中黄色点与其它各点之间的距离。这里我们使用比较常用的欧氏距离公式（Euclidean Distance）

 

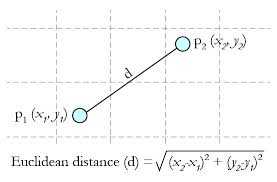
（关于距离的计算，还可以使用其它算法。）
通过计算我们得到如下数据：

表1：已知电影与未知电影的距离
电影名称	电影类型	与未知电影的距离
california Man	Romance	20.5
He‘s Not Really into Dudes	Romance	18.7
Beautiful Woman	Romance	19.2
Kevin Longblade	Action	115.3
Robo Slayer 3000	Action	117.4
Amped II	Action	118.9

 

　　若k=3，则我们取距离值最小的3个点。在这3个点中Romance类型有3个，Action类型有0个，所以Romance类型出现频率最高。因此我们判定未知类电影属于Romance类型。

3、KNN分类算法伪代码：

对未知类别属性的数据集中的每个点依次执行以下操作：
　　（1）计算已知类别数据集中的点与当前点之间的距离;
　　（2）按照距离递增次序排序;
　　（3）选取与当前点距离最小的k个点;
　　（4）确定前k个点所在类别的出现频率;
　　（5）返回前k个点出现频率最高的类别作为当前点的预测分类。

4、算法优缺点

优点：

　　算法简单，容易实现;对异常值不敏感。

缺点：

　　空间复杂度高
　　　　需要大量空间储存所有已知实例
　　计算复杂度高
　　　　需要比较所有已知实例与要分类的实例

二、实例：手写识别系统

程序运行在python3.6

 1 #-*- coding:utf-8 -*-
 2 
 3 from numpy import *
 4 import operator
 5 from os import listdir
 6 
 7 def classify(inX, dataSet, labels, k):
 8     """
 9     :param inX: 样本数据
10     :param dataSet: 已知数据
11     :param labels: 已知数据的分类标签
12     :param k:选取的k值
13     :return: 返回样本数据的分类标签
14     """
15     dataSetSize = dataSet.shape[0] #获取矩阵行数
16 
17     #计算欧氏距离
18     diffMat = tile(inX, (dataSetSize, 1)) - dataSet
19     sqDiffMat = diffMat**2
20     sqDistances = sqDiffMat.sum(axis=1)
21     distances = sqDistances**0.5
22 
23     sortedDistIndicies = distances.argsort() #对索引进行排序（从小到大）
24     classCount={}
25 
26     #选出距离最小的k个点
27     for i in range(k):
28         voteIlabel = labels[sortedDistIndicies[i]]
29         classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
30 
31         sortedClassCount = sorted(classCount.items(),
32                                   key=operator.itemgetter(1),reverse=True)
33 
34         return sortedClassCount[0][0]
35 
36 
37 def img2vector(filename):
38     """
39     :param filename: 输入文件名称，用于获取文本数据
40     :return: 将文本数据以数组形式返回
41     """
42     returnVect = zeros((1, 1024))
43     fr = open(filename)
44     for i in range(32):
45         lineStr = fr.readline()
46         for j in range(32):
47             returnVect[0,32*i+j] = int(lineStr[j])
48     return returnVect
49 
50 def handwritingClassTest():
51     hwLabels = []
52     trainingFileList = listdir(‘trainingDigits‘) #获取目录下的内容（文件名称）
53     m = len(trainingFileList)
54     trainingMat = zeros((m, 1024))
55     for i in range(m):
56         fileNameStr = trainingFileList[i]
57         fileStr = fileNameStr.split(‘.‘)[0]
58         classNumStr = int(fileStr.split(‘_‘)[0])
59         hwLabels.append(classNumStr)
60         trainingMat[i,:] = img2vector(‘trainingDigits/%s‘ % fileNameStr)
61     testFileList = listdir(‘testDigits‘)
62     errorCount = 0.0
63     mTest = len(testFileList)
64     for i in range(mTest):
65         ‘‘‘
66             对文件名字进行解析
67             此程序中使用的文件名字格式为：
68                     正确数字_编号.txt
69         ‘‘‘
70         fileNameStr = testFileList[i]
71         fileStr = fileNameStr.split(‘.‘)[0]
72         classNumStr = int (fileStr.split(‘_‘)[0])
73 
74         vectorUnderTest = img2vector(‘testDigits/%s‘ % fileNameStr) #录入测试数据
75         #对测试数据进行分类
76         classifierResult = classify(vectorUnderTest,
77                                     trainingMat, hwLabels, 3)
78         print("the classifier came back with: %d, the real answer is : %d" 79               % (classifierResult, classNumStr))
80         if (classifierResult != classNumStr):  errorCount += 1.0
81     print("the total number of errors is : %d" % errorCount)
82     print("the total error rate is : %f" % (errorCount/float(mTest)))

运行结果：

 

　　我们可以看出k-近邻算法识别手写数字程序，错误率为1.4%。

三、总结

　　kNN算法是机器学习中分类算法的一种，属于监督学习。是分类数据时最简单最有效的算法。但是执行效率低，运行非常耗时。

 

参考资料：
《机器学习实战》