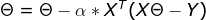梯度下降法----一种无约束的优化算法
梯度下降法----一种无约束的优化算法1.1梯度
在微积分里面,对多元函数的参数求?偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。
for example
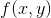
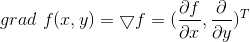
几何意义:
函数变化增加最快的方向,换句话说,沿梯度向量的方向,容易找到函数的最大值。梯度向量相反的方向,是函数减小最快的方向,容易最小值。
与最优解的关系:
梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
梯度下降的相关术语:
1. 步长(Learning rate):步长决定了在梯度下降迭代的过程中,每一步沿梯度负方向前进的长度。用上面下山的例子,步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。
2.特征(feature):指的是样本中输入部分,比如样本(x0,y0),(x1,y1),则样本特征为x,样本输出为y。
3. 假设函数(hypothesis function):在监督学习中,为了拟合输入样本,而使用的假设函数,记为hθ(x)。比如对于样本(xi,yi)(i=1,2,...n),可以采用拟合函数如下: hθ(x) = θ0+θ1x。
4. 损失函数(loss function):为了评估模型拟合的好坏,通常用损失函数来度量拟合的程度。损失函数极小化,意味着拟合程度最好,对应的模型参数即为最优参数。
1.2算法描述
1.确定优化模型的假设函数和损失函数。
2.算法参数的初始化:步长
3.process
1)初始位置的损失 函数的梯度
2)步长乘以损失函数的梯度,得到当前位置的下降距离
3)确定是否下降高度是否都小于 ![技术分享图片]() ,则终止,
,则终止,
4)跟新位置 ,跳回1),2),3)
多元回归中的,梯度下降算法:
代数形式:
假设函数:
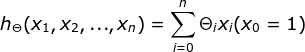
参数初始化:
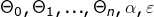
损失函数:
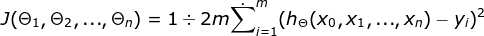
算法过程:
step1:当前位置的梯度:
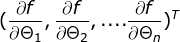
step2:步长乘以梯度
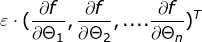
,判断梯度下降距离是否都小于
step3:更新![技术分享图片]()
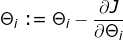
线性回归
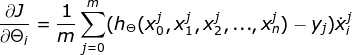
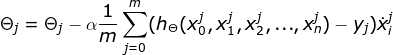
矩阵形式:
假设函数:
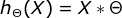
损失函数:
1)![技术分享图片]()
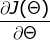
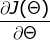
2)![技术分享图片]()
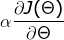
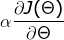
3)![技术分享图片]()
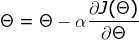
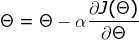
在线性回归中