神经网络理论
Posted 树的种子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了神经网络理论相关的知识,希望对你有一定的参考价值。
神经网络主要分为两种,BP神经网络,RBF神经网络
BP神经网络
-
BP神经网络的认识
其实,BP神经网络就像我们生物学中的环境系统里面的生态稳定,正反馈,负反馈。看BP神经网络的名字就知道,的确这样。(Back Propagation)
BP(Back Propagation)神经网络分为两个过程:
(1)工作信号正向传递子过程
(2)误差信号反向传递子过程
在BP神经网络中,单个样本有 m 个输入,有 n 个输出,在输入层和输出层之间还有隐含层。(拓展,已经证明了对于任何闭区间内的一个连续函数都可以用一个隐含层的BP网络来逼近,这就是万能逼近定理)。一个三层的 BP 网络就可以完成任意的 m 维到 n 为的映射。输入层,隐含层,输出层。
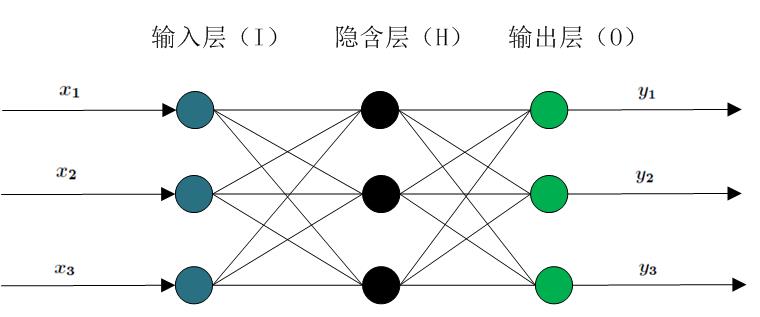
-
隐含层的选取
在BP神经网络中,输入层和输出层的节点个数都是确定的,而隐含层节点是不确定的,那么应该设置为多少才合适呢?实际上,隐含层节点个数对神经网络的性能是有影响的,一个经验公式可以确定隐含层的节点数目,如下:
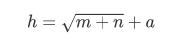
其中 h 为隐含层节点数目,m 为输入层节点数目,n 为输出层节点数目,a 为 1~ 10 之间调节的调节函数。
-
正向传递子过程
现在设节点 和节点 的权重为 ,节点 的阀值为 ,每个节点的输出值为 ,而每个节点的输出值是很复杂的,要根据:上层所有节点的输出值,当前节点与上一层所有节点的权值和,每个节点的阀值,还有激活函数来实现。
具体的计算方法如下:
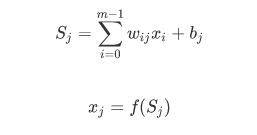
其中 f 函数是激活函数,一般选取 S 型函数或线性函数。
按照公式,正向传递即可。在输入层节点没有阀值。
-
反向传递子过程
在 BP 神经网络中,误差信号反向传递子过程比较复杂的,从我们的生物学中也是容易知道的,它是基于 Widrow-Hoff 学习规则的。假设输出层的所有结果是 ,误差函数如下:
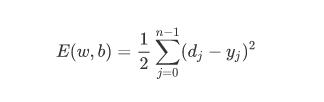
而BP神经网络的主要目的是反复修正权值和阀值,使得误差函数值达到最小。而 学习规则是通过相对误差平方和的最速下降方向,连续调整网络的权值和阀值,权值矢量的修正 比于当前位置上 的梯度,对于第 个输出节点有
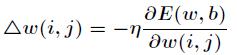
假设选择激活函数为
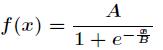
对激活函数求导,得到
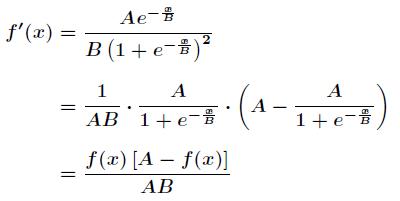
那么接下来对 Wij 有
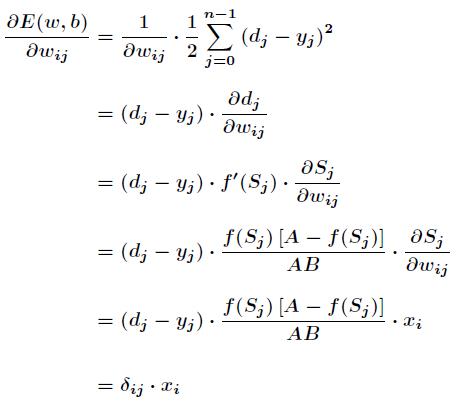
其中有
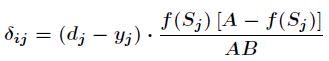
同样对于 bj 有
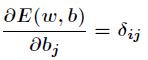
这就是著名的学习规则,通过改变神经元之间的连接权值来减少系统实际输出和期望输出的误差,这个规则又叫做学习规则或者纠错学习规则。
上面试对隐含层和输出层之间的权值和输出层的阀值计算调整量,而针对输入层和隐含层和隐含层的阀值调整的计算更为复杂。假设 Wki 是输入层第 k 个节点和隐含层第 i 个节点之间的权值,那么有:
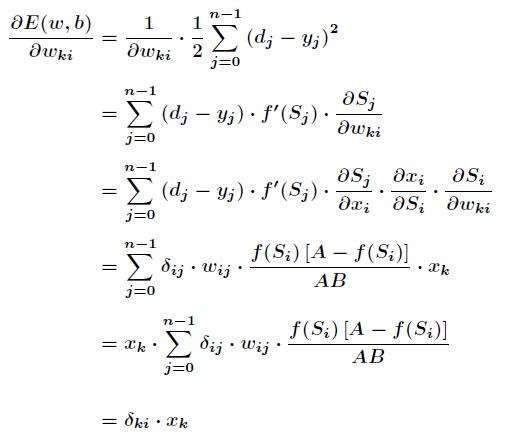
其中有
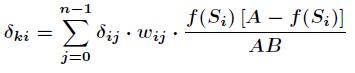
上诉两个公式,根据梯度下降法,那么隐含层和输出层之间的权值和阀值的调整如下:
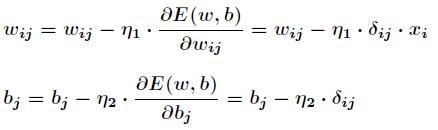
至此,BP 神经网络的原理就是这么多了,数学成分很多很多。感兴趣的还是可以研究一下,其实重点还是那句话,向着相对误差平方和下降速度最大的地方进行调整。
RBF神经网络
RBF(径向基函数)网络有很强的逼近能力,分类能力和学习速度。
-
其工作原理是
把网络看成对未知函数的逼近,任何函数都可以表示成一组基函数的加权和,也即选择各隐层神经元的传输函数,使之构成一组基函数来逼近未知函数。
RBF人工神经网络由一个输入层,一个隐含层,一个输出层组成。
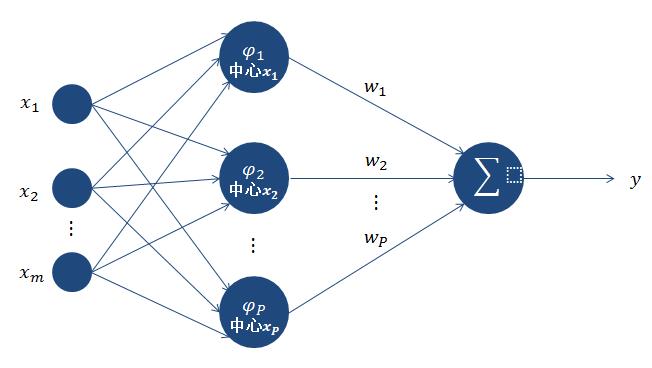
他使用径向基函数作为隐层神经元激活函数,而输出层是对隐层神经元输出的线性组合。假设输入为 d 维向量 x,输出为实值,则 RBF 网络可以表示为:
q :隐层神经元个数
ci,wi :第 i 个隐层神经元所对应的中心和权重, 是径向基函数,这是某种沿径向对称的标量函数,通常定义为样本 x 到数中心 之间的欧式距离的单调函数,常用的高斯径向基函数形如:
已经证明,具有足够多隐层神经元的 RBF 网络能以任意精度比较连续函数。
-
使用
通常采用两步来训练 RBF 网络
第一步:确定神经元中心 ,常用的方式包括随机采样,聚类等。
第二步:利用BP神经网络来确定参数 wi 和 β
参考:ACdreamers,司守奎,周志华
以上是关于神经网络理论的主要内容,如果未能解决你的问题,请参考以下文章