2.4继续说说昨天的题---关于递归的几道题目

Posted 2020-10-23 醒佳只是个Shall_ByeBye

其实递归我一直不太会用，正好这次的题目讲了再加上自己网上搜的代码把这次的两道递归题总结了一下。

第一题：第39级台阶

小明刚刚看完电影《第39级台阶》，离开电影院的时候，他数了数礼堂前的台阶数，恰好是39级!

站在台阶前，他突然又想着一个问题：

如果我每一步只能迈上1个或2个台阶。先迈左脚，然后左右交替，最后一步是迈右脚，也就是说一共要走偶数步。那么，上完39级台阶，有多少种不同的上法呢？

请你利用计算机的优势，帮助小明寻找答案。

//答案：51167078

这是第一次自己做不会做的时候，在网上搜的代码，然后自己做的注解。
主要的思想就是，现在一共有39级台阶，建立一个函数f(n,s)。n表示台阶的阶数，s表示上台阶的方案（一步走1||2）。然后39级台阶，递归，一次走1||2，知道n==0，并且步数要为偶数即s.length()%2==0

 1 public class Main {
 2     static int num=0;  
 3     public static void main(String[] args) {  
 4         f(39,"");  
 5         System.out.println(num);  
 6     }  
 7     /** 
 8      * 递归求解其中 
 9      * @param n 台阶的级数 
10      * @param s 上台阶的方案 
11      */  
12     static void f(int n,String s){  
13          
14         if(n<0){   //不符合台阶的总级数，不和题意 
15 
16             return;  
17         }
18        
19         if(n==0){   //当n=0时，刚好走完了所有的台阶  
20            
21             if(s.length()%2==0)   //当走完所有台阶的步数是偶数时  
22                
23                 num++;    //方案数量加1 
24             return;  
25         }  
26         /** 
27          * 当台阶还没有走完时，继续走下去 
28          * 每一步可以走一个台阶或者是两个台阶 
29          */  
30         for(int i=1;i<3;i++){  
31             f(n-i,s+i);  
32         }  
33     }
34 }

在讲这道题的时候和这个方法差不多，就是39->0 和 0->39的区别。我自己觉得第二种更好理解一些。然后根据自己的记忆和理解写了下面这种方法：

step->现在已经走了的台阶数，从0开始一次+1||+2

s->现在已经走了几步，1 2 3 4.。。。用于最后step==39时判断是否走了偶数步

 1 public class Main {
 2     public static int res=0;
 3     //step现在已经走了的台阶数，s现在已经走了几步
 4     public static void Do(int step,int s){
 5         if(step>39)return;
 6         if(step==39){
 7             if(s%2==0){
 8                 res++;
 9                 return;
10             }
11         }
12         s++;
13         Do(step+1,s);
14         Do(step+2,s);
15     }
16     public static void main(String[] args) {
17         // TODO Auto-generated method stub
18         Do(0,0);
19         System.out.println(res);
20     }
21 
22 }

 

第二题：振兴中华

小明参加了学校的趣味运动会，其中的一个项目是：跳格子。

地上画着一些格子，每个格子里写一个字，如下所示：（也可参见p1.jpg）

从我做起振
我做起振兴
做起振兴中
起振兴中华

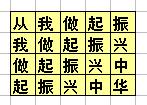
比赛时，先站在左上角的写着“从”字的格子里，可以横向或纵向跳到相邻的格子里，但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。

要求跳过的路线刚好构成“从我做起振兴中华”这句话。

请你帮助小明算一算他一共有多少种可能的跳跃路线呢？

代码：不多说了，注解也很清楚了

 1 public class Main {
 2     public static int [][] maps={//把文字转换成数字方便用
 3         {0,1,2,3,4},
 4         {1,2,3,4,5},
 5         {2,3,4,5,6},
 6         {3,4,5,6,7}
 7     };
 8     public static int res=0;
 9     //t,top指高度 l,left指宽度
10     public static void DFS(int deep,int t,int l){
11         if(t<0||t>3||l<0||l>4) return;//边界问题
12         if(maps[t][l]!=deep) return;//你走一步就是从0->1->2->3....正好和deep一样
13         if(deep==7){
14             res++;
15             return;
16         }
17         deep++;
18         DFS(deep,t+1,l);//向下走
19         DFS(deep,t,l+1);//向右走
20         
21     }
22     public static void main(String[] args) {
23         DFS(0,0,0);
24         System.out.println(res);
25     }
26     
27 }

 

另一种方法就是我一开始做题的时候用的，数数法。也能数出来。但是我没注意到这个找规律是杨辉三角，我直接截图了讲题的图应该都能看出来的。