灰色预测

Posted 2020-10-23 fangbei

灰色预测是一种对含有不确定因素的系统进行预测的方法。灰色预测通过鉴别系统因素之间发展趋势的相异程度，即进行关联分析，并对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物未来发展趋势的状况。其用等时距观测到的反应预测对象特征的一系列数量值构造灰色预测模型，预测未来某一时刻的特征量，或达到某一特征量的时间。

 

灰色预测是以灰色模型为基础的，在诸多灰色模型中，以灰色系统中单序列一阶线性微分方程模型GM(1,1)最为常用。

 

灰色模型GM(1,1)

  灰色系统理论是基于关联空间、光滑离散函数等概念定义灰导数与灰微分方程，进而用离散数据列建立微分方程形式的动态模型，即灰色模型是利用离散随机数经过生成变为随机性被显著削弱而且较有规律的生成数，建立起的微分方程形式的模型，这样便于对其变化过程进行研究和描述。

  G表示grey（灰色），M表示model（模型）

  定义x(1)的灰导数为 

  令z(1)(k)为数列x(1)的邻值生成数列，即 

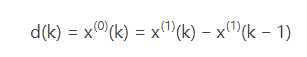
z(1)(k)=αx(1)(k)+(1−α)x(1)

  于是定义GM（1,1）的灰微分方程模型为 

d(k)+αz(1)(k)=b或x(0)(k)+αz(1)(k)=b

  其中，x(0)(k)称为灰导数，α称为发展系数，z(1)(k)称为白化背景值，b称为灰作用量。

  将时刻k=2,3,…,n代入上式有 

???????x(0)(2)+αz(1)(2)=bx(0)(3)+αz(1)(3)=b...x(0)(n)+αz(1)(n)=b

  引入矩阵向量记号： 

u=[ab]Y=??????x(0)(2)x(0)(2)...x(0)(n)??????B=??????−z(1)(2)−z(1)(3)...−z(1)(n)11...1??????

  于是GM(1,1)模型可表示为Y=Bu.

  那么现在的问题就是求a和b的值，我们可以用一元线性回归，也就是最小二乘法求它们的估计值为 

u=[ab]=(BTB)−1BTY

 

 

Python实现

 

# -*- coding: utf-8 -*-
"""
Spyder Editor

This is a temporary script file.
"""
import numpy as np
import math

raw_data = [413.05,416.51,420.47,410.01,411.87,415.91,415.5,417.28,418.75,407.86,408.68,411.25,411.88,417.7,418.12,415.3,416,416.71,427.36,424.06,416,413.12,416.02,417.9,420.3,420.6,420.46,423.75,422.57,422.28,418.5,418.47,421.32,423.74,426.59,424.75,426.01,431.48,432.04,428.51,430.03,437.76,443.85,452.26,447.8,453.69,463.02,461.77,468.14,444.85,450.46,455.32,446.6,451.11,443.73,450.39,447.38,448.4,461.18,460.2,459.87,461.56,450.7,452.28,455.01,455.76,455.8,457.89,453.01,453.24,453.52,434.55,441.57,440.81,437.48,443.51,445.03,449.09,453.95,472.01,526.02,531,532.89,530.69,536.79,538.8,570.87,572.87,574.02,585.34,576.88,583.05,575.52,580.09,614.51,672,705.87,684.5,696.99,769.5,747.95,757.6,767.3,743.9,668.6,605.85,625.8,665.5,664.87,627.42,662.33,646.61,640,674.74,674.75,705.99,659.29,681.34,667.8,677.04,640.51,664.8,648.11,649.72,647.95,667.19,653.7,659.78,665.5,665.33,683.2,674.3,675,665.85,665.01,648.04,654.03,661.82,654.17,648.47,655.51,655.93,658.34,654.99,622.83,608.29,604.1,590.28,591.27,585.5,583.73,569.41,564.64,574.17,571.83,572.21,573.51,582.1,581.42,588.01,583.54,580.32,577.2,578.02,568.55,574.17,574.78,579.49,576.15,572.73,579.85,609.89,614.52,611.5,615.23,619.75,631.73,626.25,628,612.08,611.62,614.23,613.88,611.81,610.01,607.69,613.03,609.79,600.14,597.43,597.08,603.29,602.55,600.36,609.14,605.53,603.76,604.6,611.1,614.09,609.09,612.67,610.98,614.09,613.51,620.13,620.5,616.56,618.87,641.87,637.63,637.01,643,640.2,644.18,639.79,638.68,631.77,632.46,636.73,664.99,659.03,654.65,659.52,678.7,688.67,693.47,714.51,702.55,701.02,734.6,750.85,692.51,707.62,708.89,713.95,705.55,711.99,724.54,714.87,716.22,703.57,703.64,707.43,712.17,744.98,740.67,753.97,752.9,729.67,738.99,749.85,742,737.61,740.36,731.19,724.9,731.52,731.05,739,755.36,774.88,765.46,768.5,750.62,757.36,765.01,765.01,770.5,772.9,770.21,777.99,775,774.49,777.43,784.17,790.99,790.21,790.59,797.99,829.34,859.2,918.99,895.24,898,906.4,936.43,981.7,974.74,959.26,966.58,998.99,1019.3,1037.5,1139.6,1003.2,898.5,908,915.9,903,905.76,779.54,804.58,828.12,815.3,820.74,830.1,903.99,887.46,900.29,895.74,924.02,923.72,908.52,886.1,893.35,915.12,916.7,919.43,912.55,917.35,966.19,983.73,1007,1015.7,1031.1,1006.6,1022.6,1052.1,1048.8,984.97,992,1000.1,996.01,996.5,1013.3,1013.9,1038.5,1056.2,1059.7,1056.2,1091.2,1129.6,1125.5,1189.8,1185.4,1153,1178.3,1195.5,1189.1,1233.2,1258,1289.2,1267.8,1278.4,1279.2,1232.4,1150,1190.4,1115.4,1172.4,1224.4,1238.5,1245,1256.2,1168.6,1070.4,971.51,1016.5,1040.5,1115.9,1039.1,1032.7,942.13,972.17,968.9,1042.7,1044.7,1041.8,1041.2,1081.5,1093.5,1107.5,1150.1,1145.8,1140.4,1191.5,1196.6,1188.1,1215.9,1220.3,1235.6,1227.4,1186.9,1206.8,1193.3,1212,1240,1265.4,1260.5,1308.5,1327,1346.4,1355.2,1345,1371.1,1400,1440.3,1415.6,1423.6,1435,1533,1558.5,1619,1607.1,1545.1,1597,1619.9,1703.5,1760,1796.9,1853.9,1735,1819.5,1827.3,1772,1786.2,1870,1941.5,1966.5,2059.3,2026.6,2087.3,2249.6,2395.5,2268.1,2125.9,1980.2,2056.9,2207.4,2146.7,2191.8,2312,2405.9,2461,2488.2,2636.9,2844.6,2644,2781.5,2809,2806,2941.8,2569.6,2677.1,2394.3,2377.5,2437.5,2610.1,2491.4,2582,2714.5,2624.4,2672.8,2674.9,2502.6,2483.3,2393.6,2521.2,2518.2,2472.4,2420.6,2346.2,2445.1,2524,2579.9,2598.6,2593.2,2479.3,2542,2477.9,2318.3,2283.8,2375.6,2330.1,2206.5,1978.6,1925,2220,2302.8,2253.4,2865.1,2659,2844.7,2750.1,2769.7,2560.9,2527.7381,2664.6,2784.8,2713.1,2748.2,2854.3,2731.3,2702,2790.3,2860,3252.3,3232.1,3396,3415,3340.4,3405,3643.4,3866.2,4061.6,4320.8,4151.8,4386.4,4263,4090.1,4145,4063.1,3998.2,4081.9,4130.2,4322.1,4351.5,4340.4,4332.8,4385.1,4587.1,4568,4718.3,4907.7,4532.3,4598.5,4205,4375,4595.8,4613.7,4304,4315.9,4233.9,4198.7,4149.4,3849.7,3235.3,3697.1,3681.5,3666.6,4084.4,3892.2,3872.4,3596.7,3602.3,3779.6,3654.7,3930.1,3881.5,4209.7,4190,4168,4367.1,4404.3,4400.2,4310.6,4215.9,4312,4370,4435.6,4611.9,4782.3,4777.7,4824.9,5440,5636.8,5833.5,5713.9,5764.8,5597.1,5567,5694.2,5983.8,6005.1,5981.3,5907.3,5510,5724.1,5890,5759.7,5720.3,6150,6130,6455.1]

# n = len(raw_data)
# print(n)
# # 7446.1 

min = 7
max = len(raw_data)

for i in range(max, (max - 61), -1):
    if (i > (max - min)):
        continue;
    # print(raw_data[i:998])
    history_data = raw_data[i:max]

    n = len(history_data)
    # print(n)
    X0 = np.array(history_data)

    #累加生成
    history_data_agg = [sum(history_data[0:i+1]) for i in range(n)]
    X1 = np.array(history_data_agg)

    #计算数据矩阵B和数据向量Y
    B = np.zeros([n-1,2])
    Y = np.zeros([n-1,1])
    for i in range(0,n-1):
        B[i][0] = -0.5*(X1[i] + X1[i+1])
        B[i][1] = 1
        Y[i][0] = X0[i+1]

    #计算GM(1,1)微分方程的参数a和u
    #A = np.zeros([2,1])
    A = np.linalg.inv(B.T.dot(B)).dot(B.T).dot(Y)
    a = A[0][0]
    u = A[1][0]

    #建立灰色预测模型
    XX0 = np.zeros(n)
    XX0[0] = X0[0]
    for i in range(1,n):
        XX0[i] = (X0[0] - u/a)*(1-math.exp(a))*math.exp(-a*(i));


    #模型精度的后验差检验
    e = 0      #求残差平均值
    for i in range(0,n):
        e += (X0[i] - XX0[i])
    e /= n

    #求历史数据平均值
    aver = 0;     
    for i in range(0,n):
        aver += X0[i]
    aver /= n

    #求历史数据方差
    s12 = 0;     
    for i in range(0,n):
        s12 += (X0[i]-aver)**2;
    s12 /= n

    #求残差方差
    s22 = 0;       
    for i in range(0,n):
        s22 += ((X0[i] - XX0[i]) - e)**2;
    s22 /= n

    #求后验差比值
    C = s22 / s12   
    # print(C)

    #求小误差概率
    cout = 0
    for i in range(0,n):
        if abs((X0[i] - XX0[i]) - e) < 0.6754*math.sqrt(s12):
            cout = cout+1
        else:
            cout = cout
    P = cout / n
    # print(P)

    if (C < 0.35 and P > 0.95):
        #预测精度为一级
        f = np.zeros(1)
        value = (X0[0] - u/a)*(1-math.exp(a))*math.exp(-a*(n)) 
        level = "好好"
        # m = 1   #请输入需要预测的年数
        # f = np.zeros(m)
        # print(‘往后m各年负荷为：‘)
        # f = np.zeros(m)
        # for i in range(0,m):
            # f[i] = (X0[0] - u/a)*(1-math.exp(a))*math.exp(-a*(i+n))  
            # result = f[i]
    elif(C < 0.45 and P > 0.80):
        f = np.zeros(1)
        value = (X0[0] - u/a)*(1-math.exp(a))*math.exp(-a*(n)) 
        level = "合格"
    elif(C < 0.5 and P > 0.7):
        f = np.zeros(1)
        value = (X0[0] - u/a)*(1-math.exp(a))*math.exp(-a*(n)) 
        level = "勉强"
    else:
        value = 0.0
        level = "不合"
        
    print("%3s\\t%2s\\t%10.2f"%(n, level, value))