数论的一些黑科技
Posted ---学习ing---
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数论的一些黑科技相关的知识,希望对你有一定的参考价值。
在【乔明达的省选专题】里面有很多这样的解题技巧:
把Σ*Σ类型的题O(n^2)转化∑[n/i]∑[m/i],除法下结果相同的部分合并,复杂度降低至O(√n+√m)。当然论文里的题型应该说说很经典了。这里再积累几个基础题型。
1,求前n个正整数的约数之和,即∑=σ(i) ,(i=1到n)。其中n≤10^12。
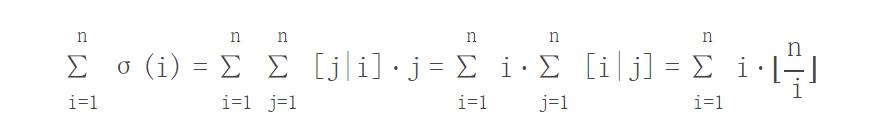
把除法下结果相同的部分合并,前面累加和用等差公式求和,复杂度为O(√n) 。
通俗理解公式: for(i=1;i<=n;i++) ans=ans+有因子i的数的个数=ans+n / i; (其中n/i=|i*1|+|i*2|+...+|i*(n/i)|,表示i是多少个数的因子)
例题: A New Function 。代码:

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<algorithm> #include<cstring> using namespace std; typedef long long ll; ll solve(int n) { ll ans=0; int B=sqrt(n); for(int i=2;i<=B;i++){ ans+=(ll)(n/i-1)*i; //前面根号n个直接暴力,由于不要1和本身,所以这里减一。 if(n/i>=B+1){ //后面合并商相同部分 ,L,R代表的是范围(个数)。 ll L=B+1,R=n/i; ans+=(L+R)*(R-L+1)/2; } } return ans; } int main() { int T,n,Case=0; scanf("%d",&T); while(T--){ scanf("%d",&n); printf("Case %d: %lld\\n",++Case,solve(n)); } return 0; }
2,求前n个正整数的莫比乌斯函数之和,即∑=u(i),其中n≤10^11
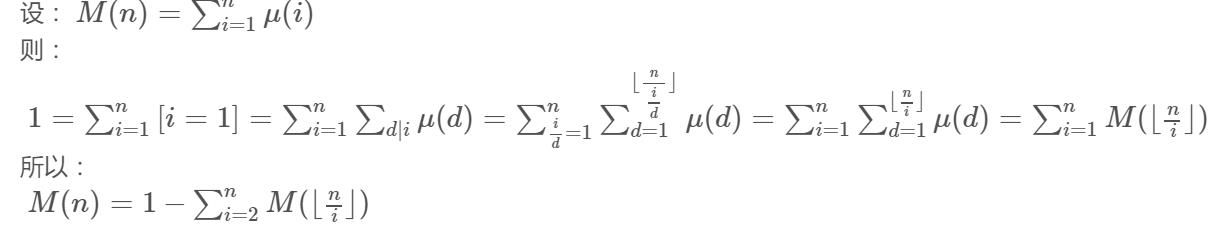
通俗理解公式:for(i=1;i<=n;i++) sum=sum+(u(1)+u(2)+u(3)+...u(j)) (其中,i*j<=n,表示以1到j为因子,i相同的合并)。 复杂度O(N^2/3)
例题:莫比乌斯函数之和 代码:

/* 技巧1:分块,在力所能及的范围里打表,范围外记得记忆化。 技巧2:注意cal函数里面的范围限定。 */ #include<map> #include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<algorithm> using namespace std; typedef long long ll; const int maxn=5000000; int mu[maxn+10],p[maxn+10],cnt; ll sum[maxn]; bool vis[maxn+10]; map<ll,ll>mp; void solve() { mu[1]=1; for(int i=2;i<=maxn;i++){ if(!vis[i]){ vis[i]=true; p[++cnt]=i; mu[i]=-1; } for(int j=1;j<=cnt&&p[j]*i<=maxn;j++){ vis[p[j]*i]=true; if(i%p[j]==0){ mu[p[j]*i]=0; break; } mu[p[j]*i]=-mu[i]; } } for(int i=1;i<=maxn;i++) sum[i]=sum[i-1]+mu[i]; } ll cal(ll n) { if(n<=maxn) return sum[n]; if(mp.find(n)!=mp.end()) return mp[n]; ll res=1,R; for(ll i=2;i<=n;i=R+1){ R=n/(n/i); res-=cal(n/i)*(R-i+1); } return mp[n]=res; } int main() { ll n,m; solve(); scanf("%lld%lld",&m,&n); printf("%lld\\n",cal(n)-cal(m-1)); return 0; }
3,欧拉函数之和,与上题差不多。就不重复了。
4,求n*m的GCD表中互素的个数和,即gcd(i,j)=1组数ans,以及ansx=Σi*i出现次数,ansy=Σj*j出现次数。T组询问。 (n,m<=1e5,T<=1e5)
那么,由莫比乌斯可得裸的方程:

while(~scanf("%d%d",&n,&m)){ ans=x=y=0; for(i=1;i<=min(n,m);i++){ ans+=mu[i]*(n/i)*(m/i); ansx+=mu[i]*i*(n/i+1)*(n/i)/2*(m/i); ansy+=mu[i]*i*(m/i+1)*(m/i)/2*(n/i); } printf("%lld %lld %lld\\n",ans,ansx,ansy); }
但是,询问过多显然超时,依照1,2,3的方法合并,使得每次询问的复杂度降低至O(√n+√m)。得:

#include<cmath> #include<cstdio> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> using namespace std; const int maxn=100000; int mu[maxn+10],p[maxn+10],sum[maxn+10],sumx[maxn+10],cnt; bool vis[maxn+10]; void get_mobi() { mu[1]=1; for(int i=2;i<=maxn;i++){ if(!vis[i]) mu[i]=-1,p[++cnt]=i; for(int j=1;j<=cnt&&p[j]*i<=maxn;j++){ vis[p[j]*i]=true; if(i%p[j]==0) { mu[p[j]*i]=0; break; } mu[p[j]*i]=-mu[i]; } } for(int i=1;i<=maxn;i++) sum[i]=sum[i-1]+mu[i],sumx[i]=sumx[i-1]+mu[i]*i; } int main() { get_mobi(); int n,m,R;long long ans,ansx,ansy; while(~scanf("%d%d",&n,&m)){ ans=ansx=ansy=0; R=0; for(int i=1;i<=min(n,m);i=R+1){ R=min(n/(n/i),m/(m/i)); ans+=(long long)(sum[R]-sum[i-1])*(n/i)*(m/i); ansx+=(long long)(sumx[R]-sumx[i-1])*(n/i)*(n/i+1)/2*(m/i); ansy+=(long long)(sumx[R]-sumx[i-1])*(m/i)*(m/i+1)/2*(n/i); } printf("%lld %lld %lld\\n",ans,ansx,ansy); } return 0; }
例题 Acdream GSD SUM 。
5,SPOJ PGCD:求n*m的GCD表中质数的个数,T组询问。 (n,m<=1e7,T<=1e3.)
和上一题一样,需要注意如何利用前缀和: 相同的合并,不相同的前缀和,方便差分得到区间和。

#include<cmath> #include<cstdio> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> using namespace std; const int maxn=10000000; int mu[maxn+10],p[maxn+10],sum[maxn+10],cnt; bool vis[maxn+10]; void get_mobi() { mu[1]=1; for(int i=2;i<=maxn;i++){ if(!vis[i]) sum[i]=1,mu[i]=-1,p[++cnt]=i; for(int j=1;j<=cnt&&p[j]*i<=maxn;j++){ vis[p[j]*i]=true; if(i%p[j]==0) { sum[p[j]*i]=mu[i]; mu[p[j]*i]=0; break; } mu[p[j]*i]=-mu[i]; sum[p[j]*i]=mu[i]-sum[i]; } sum[i]+=sum[i-1]; } } int main() { get_mobi(); int n,m,R,T;long long ans; scanf("%d",&T); while(T--){ scanf("%d%d",&n,&m); ans=0; R=0; for(int i=1;i<=min(n,m);i=R+1){ R=min(n/(n/i),m/(m/i)); ans+=(long long)(sum[R]-sum[i-1])*(n/i)*(m/i); } printf("%lld\\n",ans); } return 0; }
例题:SPOJ PGCD
6,EOJ Monthly 2018.2 (Good bye 2017)
给定一些数,求给每个数ai加xi,使得每个ai都满足ai%p=0,p未知。
枚举p,根据欧拉数p/1+p/2+p/3+...p/inf=plnp.

#include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> using namespace std; const int maxn=3000000; #define ll long long int i,j,n,k,x; ll p[maxn+10],sum[maxn+10],tmp,ans=100000000000000000,Max=0; int main() { scanf("%d%d",&n,&k); for(i=1;i<=n;i++){ scanf("%d",&x); tmp+=x; p[x]++; } if(tmp<=k){ printf("0\\n"); return 0; } for(i=1;i<=maxn;i++) { sum[i]=sum[i-1]+p[i]*i; p[i]+=p[i-1]; } for(i=2;i<=maxn;i++){ ll yy=(k-1)/i+1; ll xx=n; tmp=0; //if(k%i==0&&yy<xx) continue; if(k%i==0) continue; //上面的WA了 for(j=0;j<maxn/i;j++){ int n1=(j+1)*i,n2=j*i+1; if(n2<0) n2=0; xx+=(p[n1]-p[n2-1]); tmp+=(p[n1]-p[n2-1])*((j+1)*i)-sum[n1]+sum[n2-1]; if(k%i==0&&yy<xx) break; if(tmp>ans) break; } if((k%i==0&&xx<=yy)||k%i!=0){ ans=min(ans,tmp); } } cout<<ans<<endl;; return 0; }
//求第N个含平方因子数时,可以把二分范围限制到如此,而筛不含平方因子数的时候,可以把上界限制到2N。 #include<bits/stdc++.h> #define ll long long #define rep(i,a,b) for(int i=a;i<=b;i++) using namespace std; const int maxn=50000010; const double pi=acos(-1.0); map<int,int>M; int mu[maxn],mu2[maxn],p[maxn>>3],cnt; bool vis[maxn]; void init() { mu[1]=1; mu2[1]=1; rep(i,2,maxn-1){ if(!vis[i]) p[++cnt]=i,mu[i]=-1; for(int j=1,t;j<=cnt&&(t=p[j]*i)<maxn;j++){ mu[t]=-mu[i]; vis[t]=1; //少做几次乘法 if(!(i%p[j])) {mu[t]=0; break;} } } rep(i,2,maxn-1) mu2[i]=mu2[i-1]+(!mu[i]?0:1),mu[i]+=mu[i-1]; } int musum(int x)//莫比乌斯前缀和 { if(x<maxn) return mu[x]; if(M.count(x))return M[x]; int res=1; for(int i=2,j;i<=x;i=j+1){ int k=x/i; j=x/k; res-=musum(k)*(j-i+1); } return M[x]=res; } ll nonfsum(ll x) //无平方因子前缀和 { if(x<maxn) return mu2[x]; ll i=1,res=0,lst=0,R,t; for(;i*i*i<=x;i++) res+=(x/(i*i))*(mu[i]-lst),lst=mu[i]; for(res-=(t=x/(i*i))*lst;t;t--) res+=musum(sqrt(x/t)); return res; } int main(){ init(); ll N,ans,l,r,Mid; scanf("%lld",&N); l=N/(1-6/pi/pi),r=l+400000,l-=400000; //大致范围 l=max(l,1LL); while(l<=r){ Mid=l+r>>1; if(Mid-nonfsum(Mid)>=N) ans=Mid,r=Mid-1; else l=Mid+1; } printf("%lld\\n",ans); return 0; }
以上是关于数论的一些黑科技的主要内容,如果未能解决你的问题,请参考以下文章
