POJ 1470 -- Closest Common Ancestors

Posted 2020-10-23 _kangkang

题目链接：http://poj.org/problem?id=1470

Closest Common Ancestors

Time Limit: 2000MS		Memory Limit: 10000K
Total Submissions: 21483		Accepted: 6812

Description

Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)

Input

The data set, which is read from a the std input, starts with the tree description, in the form: 

nr_of_vertices 
vertex:(nr_of_successors) successor1 successor2 ... successorn 
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form: 
nr_of_pairs 
(u v) (x y) ... 

The input file contents several data sets (at least one). 
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.

Output

For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times 
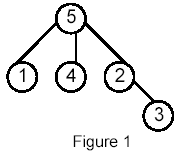
For example, for the following tree: 

Sample Input

5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)
      (2 3)
(1 3) (4 3)

Sample Output

2:1
5:5

Hint

Huge input, scanf is recommended.

 

题意：给出顶点数，各顶点的子节点数目和编号，询问次数，每次询问的顶点对，要求输出询问中出现的最近公共祖先和与其对应的询问次数；

 

题解&总结：

1. LCA裸题，下面给出Tarjan离线解法的代码，Tarjan算法网上已有许多不错的讲解，在此不再赘述，把dfs和并查集理解好Tarjan算法也就挺好理解了；

2. 输入有多组数据，注意把数组和变量初始化；

3. 输入的第一个数是节点数，不一定是根节点，根节点的确定应该通过排除子节点，剩下的一个就是根节点；

4. 代码中以前向星来储存边，当然用vector来实现邻接表也可以，但显然前向星比vector更快；

5. 题目中只给出了最大节点数，但并没有给出最大询问次数，经多次提交实验，最大询问次数应该在250000左右，注意开足够大的数组；

6. 通过此题可以发现，数组开小了不止可能会RE，还可能会访问到垃圾数据使dfs无穷递归而MLE，也可能出现死循环而TLE；

7. 题目提示推荐用scanf输入，本着倔强的精神试了cin输入也还是可以1900+MS过了。

 

 1 #include <iostream>
 2 #include <stdio.h>
 3 #include <cstring>
 4 #define N 1010
 5 #define MAXQ 250010
 6 using namespace std;
 7 struct node{
 8     int next, to, lca;
 9 } edge[2*N], qedge[2*MAXQ];  // 储存边，依次储存询问
10 int num_edge, num_qedge, head[N], qhead[N];
11 int fa[N];
12 bool vis[N], flag[N];
13 void add_edge(int from, int to) { // 前向星添加边
14     edge[++num_edge].next = head[from];
15     edge[num_edge].to = to;
16     head[from] = num_edge;
17 }
18 void add_qedge(int from, int to) {
19     qedge[++num_qedge].next = qhead[from];
20     qedge[num_qedge].to = to;
21     qhead[from] = num_qedge;
22 }
23 int Find(int x) {
24     if (fa[x] != x) fa[x] = Find(fa[x]);
25     return fa[x];
26 }
27 void dfs(int x) {
28     fa[x] = x;
29     vis[x] = true;
30     for (int k = head[x]; k; k = edge[k].next) {
31         if (!vis[edge[k].to]) {
32             dfs(edge[k].to);
33             fa[edge[k].to] = x;
34         }
35     }
36     for (int k = qhead[x]; k; k = qedge[k].next) {
37         if (vis[qedge[k].to]) {
38             qedge[k].lca = Find(qedge[k].to);
39             if (k & 1) qedge[k+1].lca = qedge[k].lca;
40             else qedge[k-1].lca = qedge[k].lca;
41         }
42     }
43 }
44 void init() {  // 初始化
45     memset(vis, false, sizeof(vis));
46     memset(flag, false, sizeof(flag));
47     memset(head, 0, sizeof(head));
48     memset(qhead, 0, sizeof(qhead));
49     num_edge = num_qedge = 0;
50 }
51 
52 int main() {
53     int n, x, y, k;
54     char ch;
55     ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
56     while (cin >> n) {
57         init();
58         for (int i = 0; i < n; i++) {
59             cin >> x >> ch >> ch >> k >> ch;//scanf("%d%*c%*c%d%*c", &x, &k);
60             while (k--) {
61                 cin >> y;//scanf(" %d", &y);
62                 flag[y] = true;
63                 add_edge(x, y); add_edge(y, x);
64             }
65 
66         }
67         cin >> k;//scanf("%d", &k);
68         for (int i = 0; i < k; i++) {
69             cin >> ch >> x >> y >> ch;//scanf(" %*c%d %d%*c", &x, &y);
70             add_qedge(x, y); add_qedge(y, x);
71         }
72         for (int i = 1; i <= n; i++) if (!flag[i]) dfs(i);  // 确定根节点
73         int cnt[N]; memset(cnt, 0, sizeof(cnt));
74         for (int i = 1; i <= k; i++) cnt[qedge[i*2].lca]++;
75         for (int i = 1; i <= n; i++) if (cnt[i]) cout << i << ‘:‘ << cnt[i] << endl;//printf("%d:%d\n", i, cnt[i]);
76     }
77 
78     return 0;
79 }

View Code