伸展树(Splay Tree)
Posted bennettz
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了伸展树(Splay Tree)相关的知识,希望对你有一定的参考价值。
伸展树是一种自平衡二叉查找树,它将每次操作的节点都旋转到根节点,伸展树操作的均摊时间复杂度为logn
基本操作
存储
struct Splay{ int key,size,num;//如果没有重复元素可不要num,如果无需维护元素排名可不要size Splay *son[2],*fa; Splay(){ memset(this,0,sizeof(Splay)); } Splay(int x){ key=x,num=size=1,fa=son[0]=son[1]=0; } }*root;
伸展操作
伸展树的最基本的操作当然就是伸展了,这也是它自平衡的基础
splay(x,S)表示在保持伸展树有序性的前提下,通过一系列旋转将伸展树S中的元素x调整至树的根部。
旋转操作就不说了
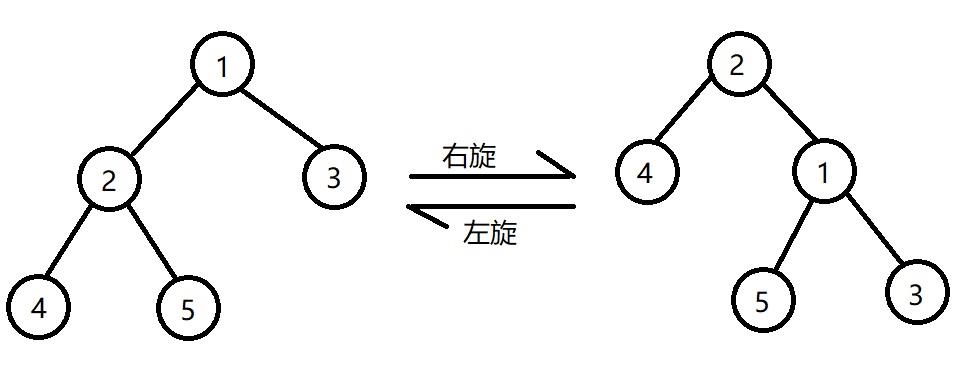
伸展操作大致分为3种情况(左右对称的算一种)
- x的父亲节点就是根节点:
这时我们只需要单次旋转(x如果是左子节点就右旋,是右子节点就左旋)将x旋转到根即可 - x的父亲节点和x同为左节点(右节点),如下图中x为4的情况:
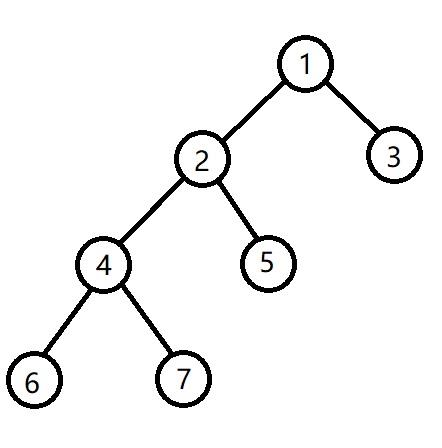
这时我们先将父节点旋转到爷爷节点
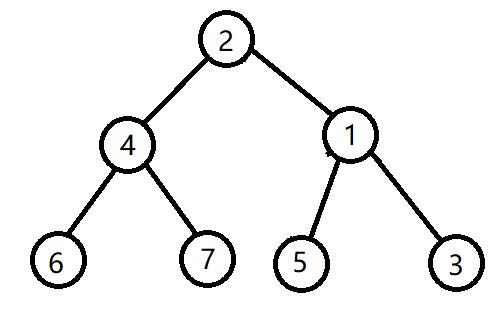
然后再将x旋转到父节点
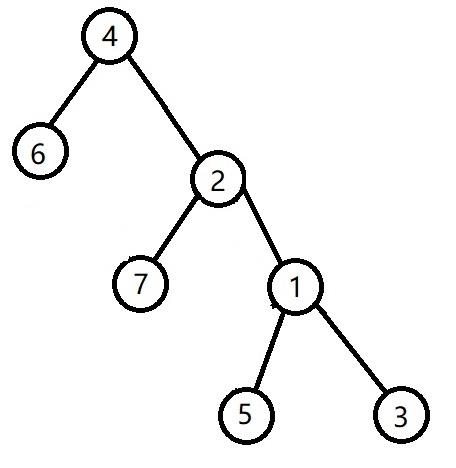
这样x就向上移了两层,然后再进行判断并继续上移直到x为根节点
- x为右子节点但x父亲为左子节点或x为左子节点但x父亲为右子节点,如下图x为5的情况:
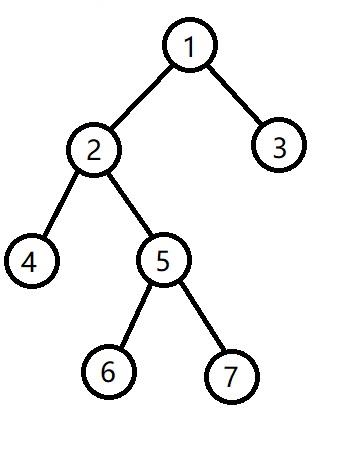
这时,可以先将x旋转到父节点
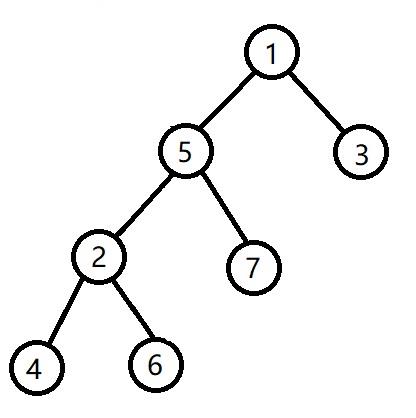
然后将x旋转到之前的爷爷节点
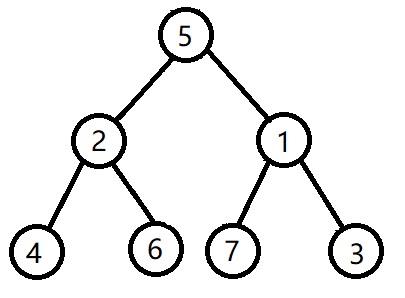
这样x也向上移了两层,然后再进行判断并继续上移直到x为根节点
下面是旋转操作和伸展操作的代码(代码中将伸展操作中2,3情况的旋转分开了,也可以将旋转合并成一次操作)
#define size(x) (x?x->size:0) #define is_r(x) (x->fa?x->fa->son[1]==x:0) void rotate(Splay *&x,int d){//将x子树旋转,d=0表示左旋,d=1表示右旋 Splay *p=x->son[!d]; x->son[!d]=p->son[d];//更新指针指向关系 if(p->son[d])p->son[d]->fa=x; p->son[d]=x,p->fa=x->fa,x->fa=p; p->size=x->size,x->size=size(x->son[0])+size(x->son[1])+x->num;//更新size值 x=p; } void up(Splay *x){//将x旋转到它的爷爷节点 bool d=is_r(x); Splay *&a=x->fa->fa->fa?x->fa->fa->fa->son[is_r(x->fa->fa)]:root;//a为指向爷爷节点的指针 if(is_r(x->fa)!=d){ rotate(a->son[!d],!d),rotate(a,d); } else rotate(a,!d),rotate(a,!d); } void splay(Splay *x,Splay *&root){//伸展操作,将x节点旋转到root节点 while(x->fa!=root&&x!=root)up(x); if(x->fa==root)rotate(root,!is_r(x)); }
插入操作
插入操作和二叉查找树的相同,只是插入过后执行伸展操作将节点旋转到根节点
void insert(Splay *&x,Splay *fa,int key){//插入key if(!x){//插入到此 x=new Splay(key),x->fa=fa,splay(x,root); return; } x->size++; if(x->key==key){x->num++,splay(x,root);return;}//树中已经有key了 int d=x->key<key; insert(x->son[d],x,key); }
合并两棵splay子树
可合并前提:一棵子树的所有元素都大于另一棵子树的所有元素
首先将较小的那棵子树的最大的元素旋转到树根,这时它一定没有右子节点,将另一棵子树接上去即可
Splay* Max(Splay *x){//返回指向x中最大的节点的指针
while(x->son[1])x=x->son[1];
return x;
}
Splay* Min(Splay *x){//返回指向x中最小的节点的指针
while(x->son[0])x=x->son[0];
return x;
}
void Merge(Splay *&x,Splay *&y){//合并x,y子树(x中所有元素>y中所有元素)
Splay *a=Max(x);//找到x中最大的节点
splay(a,x);//将x中最大的节点旋转到根
a->son[1]=y,y->fa=a;//将y接到x的右子节点
}
删除操作
将要删除的节点旋转到树根,然后合并它的两棵子树即可
Splay* Find(Splay *x,int key){//返回指向权值为key的节点的指针 if(!x)return 0; if(x->key==key)return x; return Find(x->son[key>x->key],key); } void del(Splay *&x,int key){//删除 Splay *a=Find(x,key);//找到key if(!a)return;//没找到就直接返回 splay(a,x);//将a旋转到根 if(a->num>1){a->num--,a->size--;return;}//插入不止一次,减一次即可 if(!a->son[0]){//左子节点为空,就直接用右子树替换原树 if(!a->son[1])root=NULL,delete a; else root=a->son[1],a->son[1]->fa=0,delete a;return; } if(!a->son[1]){//右子节点为空一样 root=a->son[0],a->son[0]->fa=0,delete a;return; } x=a->son[0],a->son[0]->fa=0;//合并两个子树 Merge(x,a->son[1]),delete a; }
其他操作
void mid_traversal(Splay *x){//中序遍历 if(x->son[0])mid_traversal(x->son[0]); printf("%d ",x->key); if(x->son[1])mid_traversal(x->son[1]); } int query_id(Splay *x,int key){//求数列中比key小的有几个 if(!x)return 0; if(x->key>key)return query_id(x->son[0],key); if(x->key==key)return size(x->son[0]); return query_id(x->son[1],key)+size(x->son[0])+x->num; } int query_k(Splay *x,int k){//求排第k的数 if(!x)return 0; if(size(x->son[0])>=k)return query_k(x->son[0],k); if(size(x->son[0])+x->num>=k)return x->key; return query_k(x->son[1],k-size(x->son[0])-x->num); } int ans; void pre(Splay *x,int num){//求num的前驱(即小于num的最大的数),并存在ans里 if(!x)return; if(x->key<num)ans=x->key,pre(x->son[1],num); else pre(x->son[0],num); } void suc(Splay *x,int num){//求后继 if(!x)return; if(x->key>num)ans=x->key,suc(x->son[0],num); else suc(x->son[1],num); }
#include<cstdio> #include<cstring> using namespace std; #define size(x) (x?x->size:0) #define is_r(x) (x->fa?x->fa->son[1]==x:0) struct Splay{ int key,size,num;//如果没有重复元素可不要num,如果无需维护元素排名可不要size Splay *son[2],*fa; Splay(){ memset(this,0,sizeof(Splay)); } Splay(int x){ key=x,num=size=1,fa=son[0]=son[1]=0; } }*root; void mid_traversal(Splay *x){//中序遍历 if(x->son[0])mid_traversal(x->son[0]); printf("%d ",x->key); if(x->son[1])mid_traversal(x->son[1]); } void rotate(Splay *&x,int d){//将x子树旋转,d=0表示左旋,d=1表示右旋 Splay *p=x->son[!d]; x->son[!d]=p->son[d];//更新指针指向关系 if(p->son[d])p->son[d]->fa=x; p->son[d]=x,p->fa=x->fa,x->fa=p; p->size=x->size,x->size=size(x->son[0])+size(x->son[1])+x->num;//更新size值 x=p; } void up(Splay *x){//将x旋转到它的爷爷节点 bool d=is_r(x); Splay *&a=x->fa->fa->fa?x->fa->fa->fa->son[is_r(x->fa->fa)]:root;//a为指向爷爷节点的指针 if(is_r(x->fa)!=d){ rotate(a->son[!d],!d),rotate(a,d); } else rotate(a,!d),rotate(a,!d); } void splay(Splay *x,Splay *&root){//伸展操作,将x节点旋转到root节点 while(x->fa!=root&&x!=root)up(x); if(x->fa==root)rotate(root,!is_r(x)); } void insert(Splay *&x,Splay *fa,int key){//插入key if(!x){//插入到此 x=new Splay(key),x->fa=fa,splay(x,root); return; } x->size++; if(x->key==key){x->num++,splay(x,root);return;}//树中已经有key了 int d=x->key<key; insert(x->son[d],x,key); } Splay* Max(Splay *x){//返回指向x中最大的节点的指针 while(x->son[1])x=x->son[1]; return x; } Splay* Min(Splay *x){//返回指向x中最小的节点的指针 while(x->son[0])x=x->son[0]; return x; } void Merge(Splay *&x,Splay *&y){//合并x,y子树(x中所有元素>y中所有元素) Splay *a=Max(x);//找到x中最大的节点 splay(a,x);//将x中最大的节点旋转到根 a->son[1]=y,y->fa=a;//将y接到x的右子节点 } Splay* Find(Splay *x,int key){//返回指向权值为key的节点的指针 if(!x)return 0; if(x->key==key)return x; return Find(x->son[key>x->key],key); } void del(Splay *&x,int key){//删除 Splay *a=Find(x,key);//找到key if(!a)return;//没找到就直接返回 splay(a,x);//将a旋转到根 if(a->num>1){a->num--;return;}//插入不止一次,减一次即可 if(!a->son[0]){//左子节点为空,就直接用右子树替换原树 root=a->son[1],a->son[1]->fa=0,delete a;return; } if(!a->son[1]){//右子节点为空一样 root=a->son[0],a->son[0]->fa=0,delete a;return; } x=a->son[0],a->son[0]->fa=0;//合并两个子树 Merge(x,a->son[1]),delete a; } int query_id(Splay *x,int key){//求数列中比key小的有几个 if(!x)return 0; if(x->key>key)return query_id(x->son[0],key); if(x->key==key)return size(x->son[0]); return query_id(x->son[1],key)+size(x->son[0])+x->num; } int query_k(Splay *x,int k){//求排第k的数 if(!x)return 0; if(size(x->son[0])>=k)return query_k(x->son[0],k); if(size(x->son[0])+x->num>=k)return x->key; return query_k(x->son[1],k-size(x->son[0])-x->num); } int ans; void pre(Splay *x,int num){//求num的前驱(即小于num的最大的数),并存在ans里 if(!x)return; if(x->key<num)ans=x->key,pre(x->son[1],num); else pre(x->son[0],num); } void suc(Splay *x,int num){//求后继 if(!x)return; if(x->key>num)ans=x->key,suc(x->son[0],num); else suc(x->son[1],num); } int main(){ int n,x,y;scanf("%d",&n); while(n--){ scanf("%d%d",&x,&y); switch(x){ case 1: insert(root,0,y); break; case 2: del(root,y); break; case 3: printf("%d\\n",query_id(root,y)+1); break; case 4: printf("%d\\n",query_k(root,y)); break; case 5: pre(root,y);printf("%d\\n",ans); break; default: suc(root,y);printf("%d\\n",ans); } } return 0; }
维护非有序序列的区间操作
实际上Splay Tree不只能维护有序序列,我们可以丢掉它二叉搜索树的性质,然后就可以维护非有序序列
用处:由于Splay Tree独特的伸展操作,使得它可以较快的实现对区间的操作
例题SPOJ Another Sequence Problem
存储
因为有区间操作,所以每个节点还要存标记
struct Splay{ int key,size,maxl,maxr,maxt,sum;//maxl为左区间最大值,maxr为右区间最大值, maxt为区间最大值 bool rev,same;//翻转和赋值标记 Splay *son[2],*fa; Splay(){ memset(this,0,sizeof(Splay)); } Splay(int x,Splay *f){ sum=maxl=maxr=maxt=key=x,size=1,rev=same=0,fa=f; } }
建树
每个根节点保存子树区间的中点,然后让左右子树分别保存被中点分成的两个区间
void build(Splay *&x,Splay *fa,int l,int r){//建立一棵[l,r]的子树,x指向子树的根,根的父亲为fa if(l>r)return; int mid=(l+r)>>1; x=new Splay(a[mid],fa),x->son[0]=x->son[1]=null;//根节点存区间中点 build(x->son[0],x,l,mid-1); build(x->son[1],x,mid+1,r); update(x); }
更新和下放标记
int Max(int n,...){//求n个数的max va_list arg_ptr; va_start(arg_ptr, n); int ans = -inf; for(int i=0; i < n; ++i){ int temp = va_arg(arg_ptr,int); ans=max(ans,temp); } va_end(arg_ptr); return ans; } void push_down(Splay *x){//下放标记 if(x==null)return; if(x->rev){//区间翻转 x->rev=0,x->son[0]->rev^=1,x->son[1]->rev^=1; swap(x->son[0],x->son[1]),swap(x->maxl,x->maxr); } if(x->same){//区间赋值 x->same=0,x->son[0]->key=x->son[1]->key=x->key; x->son[0]->same=x->son[1]->same=1; x->sum=x->key*x->size; x->maxl=x->maxr=x->maxt=(x->key>0?x->sum:x->key); } } void update(Splay *x){//更新节点 if(x==null)return; push_down(x),push_down(x->son[0]),push_down(x->son[1]);//要用到子节点的maxl,maxr所以要下放子节点标记 x->size=x->son[0]->size+x->son[1]->size+1,//更新节点存储的值 x->sum=x->son[0]->sum+x->son[1]->sum+x->key, x->maxl=max(x->son[0]->maxl,x->son[0]->sum+x->key+max(0,x->son[1]->maxl)), x->maxr=max(x->son[1]->maxr,x->son[1]->sum+x->key+max(0,x->son[0]->maxr)); x->maxt=Max(3,x->son[0]->maxt,x->son[1]->maxt,max(0,x->son[0]->maxr)+max(0,x->son[1]->maxl)+x->key); }
旋转和伸展
和上面的Splay相同,但旋转之前要先下放标记
void rotate(Splay *&x,int d){//旋转 Splay *p=x->son[!d]; push_down(x),push_down(p);//先下放标记 x->son[!d]=p->son[d];//更新指向关系 if(p->son[d]!=null)p->son[d]->fa=x; p->son[d]=x,p->fa=x->fa,x->fa=p; update(x),update(p);//更新节点 x=p;//x指向p指向的位置 } void up(Splay *x){//将x旋转到它的爷爷节点 bool d=is_r(x); Splay *&a=x->fa->fa->fa?x->fa->fa->fa->son[is_r(x->fa->fa)]:root;//a为指向爷爷节点的指针 if(is_r(x->fa)!=d){//x和父亲位于它们父亲的异侧 rotate(a->son[!d],!d),rotate(a,d); } else rotate(a,!d),rotate(a,!d);//x和父亲位于它们父亲的同侧 } void splay(Splay *x,Splay *&root){//将x节点旋转到root节点 if(x==null)return; while(x->fa!=root&&x!=root){ up(x); } if(x->fa==root)rotate(root,!is_r(x)); }
查找
查找分3种情况:
- 如果左子树大小$\\ge$k,则去左子树中查找第k个节点
- 如果左子树大小+1=k,则返回当前节点
- 否则去右子树中查找第k-(x->son[0]->size+1)个节点
Splay *Find(Splay *x,int k){//返回x子树中的第k个数 if(x==null)return 0; update(x); if(x->son[0]->size>=k)return Find(x->son[0],k); if(x->son[0]->size+1==k)return x; return Find(x->son[1],k-x->son[0]->size-1); }
删除
删除[l,r]区间:
- 将原树中的第l-1个数旋转到根
- 将原树中的第r+1个数旋转到根的右子节点
- 这时根的右子节点的左子树即为要删除的区间
因为l,r可能是总区间的端点,l-1,r+1会越界,所以我们在区间的两端建两个空节点
实际操作为第l个数旋转到根,将第r+2个数旋转到根的右子节点(整体右移一个节点),下面的操作相同
void remove(Splay *x){//删除x子树 if(x==null)return; remove(x->son[0]),remove(x->son[1]),delete x; } void del(int l,int r){//删除[l,r] splay(Find(root,l),root);//将l-1旋转到root splay(Find(root,r+2),root->son[1]);//将r+1旋转到root的右儿子 remove(root->son[1]->son[0]),root->son[1]->son[0]=null,update(root->son[1]),update(root);//r+1的左儿子即为区间[l,r] }
插入
在x后面插入y个数:
- 将原树中的第x个数旋转到根
- 将原树中的第x+1个数旋转到根的右子节点
- 建一棵Splay保存这y个数
- 将新建的树接到根的右子节点的左子节点上
void insert(int l,int s){//在l后面插入长为s的区间 for(int i=0;i<s;i++){ scanf("%d",a+i); } splay(Find(root,l+1),root),splay(Find(root,l+2),root->son[1]);//将l旋转到root,将l+1旋转到root的右儿子,这时l+1没有左儿子 build(root->son[1]->son[0],root->son[1],0,s-1),update(root),update(root->son[1]);//建树,更新 }
其他操作
基本所有的对区间的操作都有两个相同的步骤:
- 将原树中的第l-1个数旋转到根
- 将原树中的第r+1个数旋转到根的右子节点
这样根的右子节点的左子树即为[l,r],直接操作即可
void modify(int l,int r,int s){//将[l,r]都赋值为s splay(Find(root,l),root);//将l-1旋转到root splay(Find(root,r+2),root->son[1]);//将r+1旋转到root的右儿子 Splay *x=root->son[1]->son[0];//r+1的左儿子即为区间[l,r],打标记更新 x->same=1,x->key=s,update(root->son[1]),update(root);splay(x,root); } void rev(int l,int r){//将[l,r]翻转 splay(Find(root,l),root);//将l-1旋转到root splay(Find(root,r+2),root->son[1]);//将r+1旋转到root的右儿子 root->son[1]->son[0]->rev=1;//r+1的左儿子即为区间[l,r],打标记更新 update(root->son[1]),update(root); } int get_sum(int l,int r){//求[l,r]的和 splay(Find(root,l),root); splay(Find(root,r+2),root->son[1]); return root->son[1]->son[0]->sum; } int max_sum(){//求最大的区间值 update(root); return root->maxt; }
完整代码
#include<cstdio> #include<cstring> #include<algorithm> #include<stdarg.h> using namespace std; #define inf 0x3fffffff #define is_r(x) (x->fa?x->fa->son[1]==x:0) struct Splay{ int key,size,maxl,maxr,maxt,sum;//maxl为左区间最大值,maxr为右区间最大值, maxt为区间最大值 bool rev,same;//翻转和赋值标记 Splay *son[2],*fa; Splay(){ memset(this,0,sizeof(Splay)); } Splay(int x,Splay *f){ sum=maxl=maxr=maxt=key=x,size=1,rev=same=0,fa=f; } }*root,*null=new Splay; int a[500005]; //下面的宏在<stdarg.h>提供的有 //typedef char * va_list;//指针 //#define _ADDRESSOF(n) ( &reinterpret_cast<const char &>(n) ) //取n的地址并转为char* //#define _INTSIZEOF(n) ((sizeof(n)+sizeof(int)-1)&~(sizeof(int) - 1) ) //将sizeof(n)向上取至sizeof(int)的整数倍,在我电脑上必须*2才行 //#define va_start(ap,v) ( ap = (va_list)&v + _INTSIZEOF(v) ) //求第一位的地址存在ap中 //#define va_arg(ap,t) ( *(t *)((ap += _INTSIZEOF(t)) - _INTSIZEOF(t)) ) //取出ap的值,并将ap指向下一个位置 //#define va_end(ap) ( ap = (va_list)0 ) //置空ap int Max(int n,...){//求n个数的max va_list arg_ptr; va_start(arg_ptr, n); int ans = -inf; for(int i=0; i < n; ++i){ int temp = va_arg(arg_ptr,int); ans=max(ans,temp); } va_end(arg_ptr); return ans; } 以上是关于伸展树(Splay Tree)的主要内容,如果未能解决你的问题,请参考以下文章