机器学习-有监督-SVM

Posted 2020-10-22 米小粥

2018.1.16
给定训练集\\(T={(x_1,y_1),(x_2,y_2),\\cdots,(x_N,y_N)}\\)，一共有N个样本点。

一、线性可分的支持向量机

假定训练集是线性可分的。学习的目标是在特征空间找到一个分离超平面\\(wx+b=0\\)，能够将所有的样本正确划分为两类。学习的策略是间隔最大化。

1 目标函数

样本点\\((x_i,y_i)\\)到超平面\\(wx+b=0\\)的距离是

\\[d= \\frac{|wx_i+b|}{\\|w\\|} \\]

正例样本的\\(y_i=+1\\)，负例样本的\\(y_i=-1\\)，这样表示距离可以把绝对值符号去掉：

\\[d= \\frac{y_i(wx_i+b)}{\\|w\\|} \\]

\\(y_i(wx_i+b)\\)称为点\\((x_i,y_i)\\)到超平面\\(wx+b=0\\)的函数间隔。
所有样本点中离分离超平面最近的那个样本点的距离是：

\\[\\min \\limits_{i} {\\frac{y_i(wx_i+b)}{\\|w\\|}} \\]

在所有超平面中能让这个最小距离最大的那个w,b就是我们要的结果：

\\[\\max \\limits_{w,b} \\min \\limits_i {\\frac{y_i(wx_i+b)}{\\|w\\|}} \\]

为了方便求解，做如下变换：
对于\\(\\min \\limits_{i} {\\frac{y_i(wx_i+b)}{\\|w\\|}}\\)这部分，假设点\\((x_m,y_m)\\)取得最小距离为\\(d_0\\)，也就是\\(d_0 = {\\frac{y_m(wx_m+b)}{\\|w\\|}}\\)，对分子分母同时乘以或除以一个数，使得分子=1，也就是函数间隔=1，这时分母也发生了相应变化，因为\\(w\\)表示超平面wx+b=0的法向量方向，按比例缩放后方向没有变化，我们将变化后的分母还记作\\(\\|w\\|\\)。通过令最小函数间隔=1，目标函数变为：

\\[\\begin{aligned} &\\max \\limits_{w,b} {\\frac{1}{\\|w\\|}}\\\\ s.t. \\qquad & {y_i(wx_i+b)}\\geq 1,\\quad i=1,2,\\cdots,N \\end{aligned} \\]

约束条件保证了所有点都能分类正确。
为方便求解，进一步变化为：

\\[\\begin{aligned} &\\min \\limits_{w,b} \\frac{1}{2}\\|w\\|^2\\\\ s.t. \\qquad &{y_i(wx_i+b)} \\geq 1, \\quad i=1,2,\\cdots,N \\end{aligned} \\]

2 拉格朗日乘子法求解

2.1 构造拉格朗日函数：

\\[L(w,b,\\alpha)= \\frac{1}{2}\\|w\\|^2-\\sum_{i=1}^{N}\\alpha_i[y_i(wx_i+b)-1] \\]

其中\\(\\alpha = (\\alpha_1,\\alpha_2,\\cdots,\\alpha_N)^T\\)是拉格朗日乘子，\\(\\alpha_i \\geq 0\\)
2.2 把w,b看作常数，构造一个函数 \\(\\theta\\)定义为 \\(L(w,b,\\alpha)\\) 关于 \\(\\alpha\\) 求最大值

\\[\\theta = \\max \\limits_{\\alpha} L(w,b,\\alpha) \\]

因为 \\(\\alpha_i \\geq 0\\) 且 \\({y_i(wx_i+b)} \\geq 1\\)，所以

\\[\\theta = \\max \\limits_{\\alpha} L(w,b,\\alpha) = \\frac{1}{2}\\|w\\|^2 \\]

2.3 原始问题 \\(\\min \\limits_{w,b} \\frac{1}{2}\\|w\\|^2\\)等价于 $ \\min \\limits_{w,b} \\max \\limits_{\\alpha} L(w,b,\\alpha) \\quad$。
根据拉格朗日对偶性，问题可变为 \\(\\max \\limits_{\\alpha} \\min \\limits_{w,b} L(w,b,\\alpha)\\)
(1) 求\\(\\min \\limits_{w,b} L(w,b,\\alpha)\\)
\\(\\qquad\\)对w,b分别求偏导数：

\\[\\begin{aligned} \\frac{\\partial L}{\\partial w} &= w - \\sum_{i=1}^{N}\\alpha_i y_i x_i \\\\ \\frac{\\partial L}{\\partial b} &= -\\sum_{i=1}^{N}\\alpha_i y_i \\end{aligned} \\]

\\(\\qquad\\)令偏导数=0得到：

\\[\\begin{aligned} &w = \\sum_{i=1}^{N}\\alpha_i y_i x_i \\\\ & \\sum_{i=1}^{N}\\alpha_i y_i = 0 \\end{aligned} \\]

\\(\\qquad\\)将这两个式子带回拉格朗日函数\\(L(w,b,\\alpha)\\)得到：

\\[ L(w,b,\\alpha)= -\\frac{1}{2} \\sum_{i=1}^{N}\\sum_{j=1}^{N} \\alpha_i\\alpha_j y_i y_j (x_i x_j) + \\sum_{i=1}^{N} \\alpha_i \\]

(2) 求 \\(\\min \\limits_{w,b} L(w,b,\\alpha)\\) 对\\(\\alpha\\)的极大，$\\max \\limits_{\\alpha} { {-\\frac{1}{2} \\sum_{i=1}^{{N}\\sum_{j=1}}{N} \\alpha_i\\alpha_j y_i y_j (x_i x_j) + \\sum_{i=1}^{N} \\alpha_i} } $ ,加负号得到：

\\[\\begin{aligned} \\min \\limits_{\\alpha} & {\\frac{1}{2} \\sum_{i=1}^{N}\\sum_{j=1}^{N} \\alpha_i\\alpha_j y_i y_j (x_i x_j) - \\sum_{i=1}^{N} \\alpha_i} \\\\ s.t. \\qquad & \\sum_{i=1}^{N} {\\alpha_i y_i}=0\\\\ &\\alpha_i \\geq 0, i=1,2,\\cdots, N \\end{aligned} \\]

(3) 假设求出了(2)中 $\\alpha $ 的最优解 \\(\\alpha^* =(\\alpha_1^*,\\alpha_2^*,\\cdots,\\alpha_N^*)^T\\)
\\(w\\)的解为\\(w^*=\\sum_{i=1}^{N} \\alpha_i^* y_i x_i\\)
选择\\(\\alpha_i^*\\)的一个正分量\\(\\alpha_i^*>0\\),b的解为 \\(b*=y_j -w^*x_j=y_j - \\sum \\alpha_i^* y_i (x_i x_j)\\)

3 支持向量物理意义

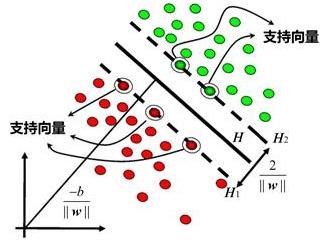
在线性可分情况下，训练集的样本点中与分离超平面距离最近的样本点称为支持向量，即使得等式成立的样本点：\\(y_i(wx_i+b)-1=0\\).对正例点，支持向量在超平面\\(H1:wx_i+b=1\\)；对负例点，支持向量在超平面\\(H2:wx_i+b=-1\\).支持向量就是落在超平面H1和H2上的点。H1和H2称为间隔边界。间隔带的宽度是\\(\\frac{2}{\\|w\\|}\\)。联系目标函数最小化\\(\\|w\\|\\)也就是要间隔最宽。 支持向量决定了模型，移动支持向量以外的样本点不影响结果，所以SVM实际上只用到了少数的样本点。但距离超平面最近的点刚好是噪声点，那么模型就会有问题。

二、线性不可分的支持向量机

1 为什么加入松弛变量

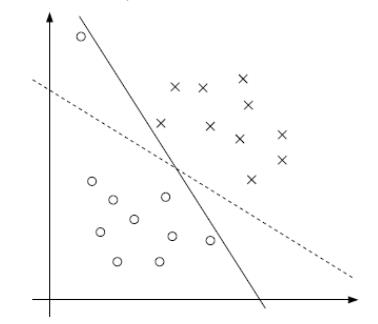
不一定完全分类正确的超平面就是最好的，如下图。用第一部分的硬间隔最大化找出的分界面很可能如实线所示，实线可以将训练数据分为两类，但其泛化能力不如虚线。

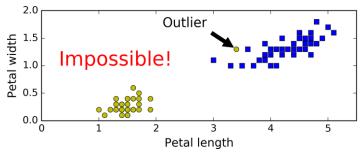
少数特异点outlier造成训练数据不是线性可分的，如下图。用第一部分的硬间隔最大化不能找出一个分界面。如果能忽视outlier，就能较好分类。

上面两张图反映了硬间隔最大化存在一些问题，所以为每个样本点引入一个松弛变量，硬间隔修改为软间隔，这就是线性不可分的支持向量机。

2 目标函数和约束

\\[\\begin{aligned} \\min \\limits_{w,b, \\xi} \\quad \\frac{1}{2}\\|w\\|^2 & +C \\sum_{i=1}^{N} \\xi_i\\\\ s.t. \\qquad {y_i(wx_i+b) + \\xi_i} & \\geq 1, \\quad i=1,2,\\cdots,N\\\\ \\xi_i & \\geq 0, \\quad i=1,2,\\cdots,N\\\\ \\end{aligned} \\]

约束条件：为每个样本点引入一个松弛变量\\(\\xi_i \\geq 0\\)使得函数间隔加上松弛\\(\\xi_i\\)不小于1。如果样本点的函数间隔本身大于1，那么\\(\\xi_i=0\\); 如果样本点的函数间隔<1，那么\\(\\xi_i=1-y_i(wx_i+b)>0\\)。

目标函数：\\(\\sum_{i=1}^{N} \\xi_i\\)代表误差，误差越小越好；\\(\\|w\\|\\)和间隔有关，\\(\\|w\\|\\)越小，间隔越宽。C是超参数，用来调节两者关系；C取得越大，对误分类的惩罚越大，当C趋于无穷大，目标函数就退化为第一部分的硬间隔最大化的目标函数；一般C取得小一些，允许训练集的少数点被分类错，从而可以达到比较好的泛化能力。

3 拉格朗日乘子法求解

3.1 构造拉格朗日函数：

\\[L(w,b,\\xi,\\alpha,\\mu)= \\frac{1}{2}\\|w\\|^2 +C \\sum_{i=1}^{N} \\xi_i-\\sum_{i=1}^{N}\\alpha_i[y_i(wx_i+b)+\\xi_i -1]-\\sum_{i=1}^{N}\\mu_i\\xi_i \\]

其中\\(\\alpha = (\\alpha_1,\\alpha_2,\\cdots,\\alpha_N)^T\\)是拉格朗日乘子，\\(\\alpha_i \\geq 0\\); \\(\\mu = (\\mu_1, \\mu_2, \\cdots, \\mu_N)^T\\)也是拉格朗日乘子，\\(\\mu_i \\geq 0\\)。
3.2 把w,b,\\(\\xi\\)看作常数，构造一个函数 \\(\\theta\\) 定义为\\(L(w,b,\\xi,\\alpha,\\mu)\\)关于\\(\\alpha, \\mu\\)求最大值

\\[\\theta = \\max \\limits_{\\alpha,\\mu} L(w,b,\\xi,\\alpha,\\mu)=\\frac{1}{2}\\|w\\|^2+C \\sum_{i=1}^{N} \\xi_i \\]

3.3 原始问题 $ \\quad \\min \\limits_{w,b} \\frac{1}{2}|w|^2 +C \\sum_{i=1}^{N}\\xi_i \\quad$等价于 $ \\quad \\min \\limits_{w,b,\\xi} \\max \\limits_{\\alpha,\\mu} L(w,b,\\xi,\\alpha,\\mu) \\quad$。
根据拉格朗日对偶性，问题可变为 $ \\quad \\max \\limits_{\\alpha,\\mu} \\min \\limits_{w,b,\\xi} L(w,b,\\xi,\\alpha,\\mu) \\quad$
(1) 求\\(\\min \\limits_{w,b,\\xi} L(w,b,\\xi,\\alpha,\\mu) \\quad\\)
对w,b,\\(\\xi_i\\)分别求偏导数：

\\[\\begin{aligned} \\frac{\\partial L}{\\partial w} &= w - \\sum_{i=1}^{N}\\alpha_i y_i x_i\\\\ \\frac{\\partial L}{\\partial b} &= -\\sum_{i=1}^{N}\\alpha_i y_i\\\\ \\frac{\\partial L}{\\partial \\xi_i} &= C-\\alpha_i - \\mu_i \\end{aligned} \\]

\\(\\qquad\\)令偏导数=0得到：

\\[\\begin{aligned} &w = \\sum_{i=1}^{N}\\alpha_i y_i x_i\\\\ &\\sum_{i=1}^{N}\\alpha_i y_i = 0\\\\ &C-\\alpha_i - \\mu_i = 0\\\\ \\end{aligned} \\]

\\(\\qquad\\)将这三个式子带回拉格朗日函数\\(L(w,b,\\xi,\\alpha,\\mu)\\)得到：

\\[ L(w,b,\\xi,\\alpha,\\mu)= -\\frac{1}{2} \\sum_{i=1}^{N}\\sum_{j=1}^{N} \\alpha_i\\alpha_j y_i y_j (x_i x_j) + \\sum_{i=1}^{N} \\alpha_i \\]

(2) 求 \\(\\min \\limits_{w,b,\\xi} L(w,b,\\xi,\\alpha,\\mu)\\) 对 \\(\\alpha,\\mu\\) 的极大，\\(\\max \\limits_{\\alpha,\\mu} \\{-\\frac{1}{2} \\sum_{i=1}^{N}\\sum_{j=1}^{N} \\alpha_i\\alpha_j y_i y_j (x_i x_j) + \\sum_{i=1}^{N} \\alpha_i\\}\\) ,加负号得到：

\\[\\begin{aligned} \\min \\limits_{\\alpha,\\mu} & {\\frac{1}{2} \\sum_{i=1}^{N}\\sum_{j=1}^{N} \\alpha_i\\alpha_j y_i y_j (x_i x_j) - \\sum_{i=1}^{N} \\alpha_i}\\\\ s.t. \\qquad & \\sum_{i=1}^{N} {\\alpha_i y_i}=0\\\\ &C-\\alpha_i - \\mu_i =0 \\\\ & \\alpha_i \\geq 0,\\\\ & i=1,2,\\cdots,N. \\end{aligned} \\]

消去\\(\\mu_i\\),从而只剩下 \\(\\alpha_i\\)，得到:

\\[\\begin{aligned} \\min \\limits_{\\alpha} &{\\frac{1}{2} \\sum_{i=1}^{N}\\sum_{j=1}^{N} \\alpha_i\\alpha_j y_i y_j (x_i x_j) - \\sum_{i=1}^{N} \\alpha_i}\\\\ s.t. \\qquad &\\sum_{i=1}^{N} {\\alpha_i y_i}=0\\\\ &0 \\leq \\alpha_i \\leq C,\\\\ &i=1,2,\\cdots, N. \\end{aligned} \\]

(3) 假设求出了(2)中 \\(\\alpha\\) 的最优解 \\(\\alpha^* =(\\alpha_1^*,\\alpha_2^*,\\cdots,\\alpha_N^*)^T\\)
\\(w\\) 的解为 \\(w^*=\\sum_{i=1}^{N} \\alpha_i^* y_i x_i\\)
选择 $ \\alpha_i^* $ 的一个正分量 $ 0<\\alpha_i^*<C $ , b的解为 \\(b*=y_j -w^*x_j=y_j - \\sum \\alpha_i^* y_i (x_i x_j)\\)

4 支持向量物理意义

支持向量物理意义:
在线性不可分的情况下，支持向量不仅包括落在间隔边界上的样本点，还包括落在间隔带内的样本点以及误分类的点。落在间隔边界的点，\\(\\xi_i=0,\\alpha_i<C\\) .落在间隔带内的点或者误分类的点，\\(\\xi_i>0,\\alpha_i=C\\).

参数C和\\(\\gamma\\)的影响直观理解：
http://blog.csdn.net/robin_xu_shuai/article/details/77051258
C越大，对错误分类的惩罚越大，容忍越小。

三、非线性的支持向量机

常用核函数：
多项式核函数
高斯核函数