 ?
?
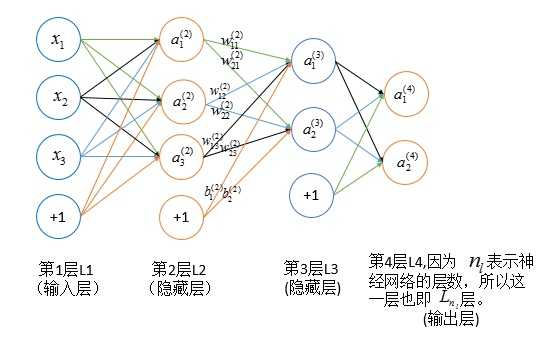
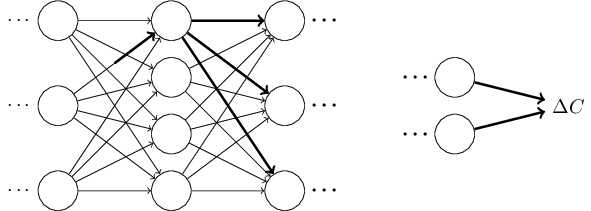
神经网络中权重 \\(w^{(l)}_{ij}\\) 的改变将影响到一个个下一层,到达输出层,最终影响代价函数
 ?
?
\\(\\color{red}{公式推导符号说明}\\)
| 符号 | 说明 |
|---|---|
| \\(n_l\\) | 网络层数 |
| \\(y_j\\) | 输出层第 \\(j\\) 类 label |
| \\(S_l\\) | 第 \\(l\\) 层神经元个数(不包括偏置) |
| \\(g(x)\\) | 激励函数 |
| \\(w^{(l)}_{ij}\\) | 第 \\(l\\) 层第 \\(j\\) 个单元与第 \\(l+1\\) 层第 \\(i\\) 个单元之间的链接参数 |
| \\(b^{(l)}_i\\) | 第 \\(l+1\\) 层第 \\(i\\) 个单元的偏置 |
| \\(z^{(l)}_i\\) | 第 \\(l\\) 层第 \\(i\\) 个单元的输入加权和(包含偏置) |
| \\(a^{(l)}_i\\) | 第 \\(l\\) 层第 \\(i\\) 个单元的激活值(输出值) |
| \\(\\delta^{(l)}_i\\) | 第 \\(l\\) 层第 \\(i\\) 个单元的局部梯度(或称为残差) |
\\(\\color{red}{基本公式}\\)
\\[ \\begin{align*} z^{(l)}_i &= b^{(l-1)}_i + \\sum^{S_l}_{j=1}{w^{(l-1)}_{ij}a^{(l-1)}_i} \\tag{1} \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\quad \\ g(x) &= \\frac{1}{1 + e^{-x}} \\tag{2}\\ a^{(l)}_i &= g(z^{(l)}_i) \\tag{3} \\ J(\\theta) &= \\frac12{{\\sum^{S_l}_{j=1}\\big ({y_j - a^{(l)}_j}}}\\big)^2 \\tag{4}\\ \\delta^{(l)}_i &=\\frac{\\partial{J(\\theta)}}{\\partial{z^{(l)}_i}} \\tag{5} \\ \\ \\delta ^{ (n_{ l }) }_{ i }&=\\frac { \\partial { J(\\theta ) } }{ \\partial { z^{ (n_{ l }) }_{ i } } } \\\\ &=\\frac { 1 }{ 2 } \\frac { \\partial { } }{ \\partial { z^{ (n_{ l }) }_{ i } } } \\sum _{ j=1 }^{ S_{ n_l } } \\left( y_{ j }-a^{ (n_{ l }) }_{ j } \\right) ^{ 2 }\\\\ &=\\frac { 1 }{ 2 } \\frac { \\partial { } }{ \\partial { z^{ (n_{ l }) }_{ i } } } \\sum _{ j=1 }^{ S_{ n_l } } \\left( y_{ j }-g(z^{ (n_{ l }) }_{ j }) \\right) ^{ 2 }\\\\ &=\\frac { 1 }{ 2 } \\frac { \\partial { } }{ \\partial { z^{ (n_{ l }) }_{ i } } } \\left( y_{ i }-g(z^{ (n_{ l }) }_{ i }) \\right) ^{ 2 }\\\\ &=-\\left( y_{ i }-a^{ (n_{ l }) }_{ i } \\right) g\\prime (z^{ (n_{ l }) }_{ i })\\\\ \\\\delta ^{ (l) }_{ i }&=\\frac { \\partial { J(\\theta ) } }{ \\partial { z^{ (l) }_{ i } } } \\\\ &=\\sum _{ j=1 }^{ S_{ l+1 } } \\frac { \\partial { J(\\theta ) } }{ \\partial { z^{ (l+1) }_{ j } } } \\frac { \\partial { z^{ (l+1) }_{ j } } }{ \\partial { z^{ (l) }_{ i } } } \\\\ &=\\sum _{ j=1 }^{ S_{ l+1 } } \\delta ^{ (l) }_{ i }\\frac { \\partial { z^{ (l+1) }_{ j } } }{ \\partial { z^{ (l) }_{ i } } } \\\\ &=\\sum _{ j=1 }^{ S_{ l+1 } } \\delta ^{ (l) }_{ i }\\frac { \\partial { } }{ \\partial { z^{ (l) }_{ i } } } \\left( b^{ (l) }_{ i }+\\sum _{ k=1 }^{ S_{ l } } w^{ (l) }_{ jk }a^{ (l) }_{ k }) \\right) \\\\ &=\\sum _{ j=1 }^{ S_{ l+1 } } \\delta ^{ (l) }_{ i }\\frac { \\partial { } }{ \\partial { z^{ (l) }_{ i } } } \\left( b^{ (l) }_{ i }+\\sum _{ k=1 }^{ S_{ l } } w^{ (l) }_{ jk }g(z^{ (l) }_{ k }) \\right) \\\\ &=\\sum _{ j=1 }^{ S_{ l+1 } } \\delta ^{ (l) }_{ i }\\frac { \\partial { } }{ \\partial { z^{ (l) }_{ i } } } \\left( w^{ (l) }_{ ji } g(z^{ (l) }_{ i }) \\right) \\&=\\sum _{ j=1 }^{ S_{ l+1 } } \\delta ^{ (l) }_{ i }\\left( w^{ (l) }_{ ji }g\\prime (z^{ (l) }_{ i }) \\right) \\\\ &=g\\prime (z^{ (l) }_{ i })\\sum _{ j=1 }^{ S_{ l+1 } } \\delta ^{ (l) }_{ i }w^{ (l) }_{ ji }\\\\\\frac { \\partial { J(\\theta ) } }{ \\partial { w^{ (l) }_{ ij } } } &=\\frac { \\partial { J(\\theta ) } }{ \\partial { z^{ (l+1) }_{ i } } } \\frac { \\partial { z^{ (l+1) }_{ i } } }{ \\partial { w^{ (l) }_{ ij } } } \\\\ &=\\delta ^{ (l+1) }_{ i }\\frac { \\partial { z^{ (l+1) }_{ j } } }{ \\partial { w^{ (l) }_{ ij } } } \\\\ &=\\delta ^{ (l+1) }_{ i }\\frac { \\partial { } }{ \\partial { w^{ (l) }_{ ij } } } \\left( b^{ (l) }_{ i }+\\sum _{ k=1 }^{ S_{ l } } w^{ (l) }_{ ik }a^{ (l) }_{ k }) \\right) \\\\ &=\\delta ^{ (l+1) }_{ i }a^{ (l) }_{ j }\\\\frac { \\partial { J(\\theta ) } }{ \\partial { b^{ (l) }_{ i } } } &=\\delta ^{ (l+1) }_{ i } \\end{align*} \\]