AC自动机（附洛谷P3769模板题）

Posted 2020-10-22 oyjason

首先，介绍一下AC自动机(Aho-Corasick automaton)，是一种在一个文本串中寻找每一个已给出的模式串的高效算法。

在学习AC自动机之前，你需要先学习Trie树和KMP算法，因为AC自动机正式利用并结合了两者的思想。

说到实际的不同，其实AC自动机只是在Trie树上引入了一个类似KMP中next数组的东西叫做Fail指针。

对于每一个节点，Fail指针指向该节点所代表的字符串中，次长的、在Trie树中存在的后缀（因为最长的在Trie树种存在的后缀就是其本身）所代表的节点。

举例：

 

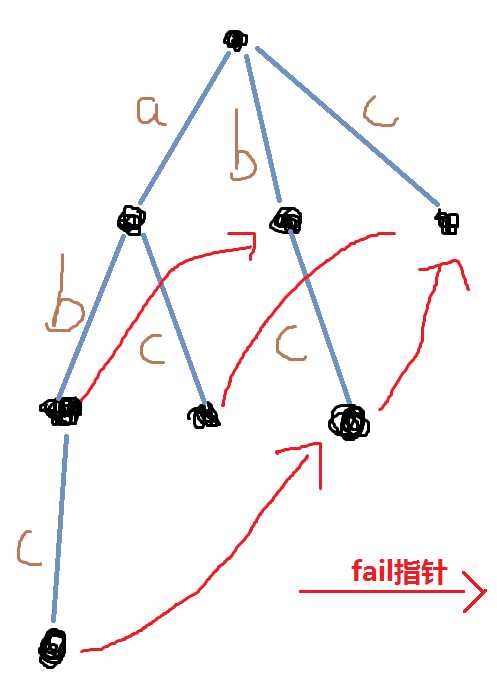
如图，字符串abc在Trie树中次长后缀为bc，bc在Trie树中次长后缀为c等等，是不是跟KMP算法中的next数组十分的相像？

那么，如何求一个节点的fail指针呢？

首先，必须先建完整棵Trie树，然后，对于跟节点，它所代表的字符串是空串，有唯一的后缀（也是空串），所以根本不存在空串，我们将它的fail指针指向-1。

接着，对于深度为1的节点，他们所代表的字符串有且只有一个字符，所以他们也没有次长后缀，但是由于要进行匹配的缘故，为了能让下一次匹配上，我们不得不将他们的fail指针指向根节点。（上图未作标注）

最后，对于深度大于等于2的某一个节点p，我们发现，它最终应当指向的那个节点q的父节点指向的字符串一定是p的父节点所对应的字符串的后缀，所以，我们可以先设p的父节点通过字母x连向p，再找到p的父节点fail指针指向的节点a，看a有没有通过字母x所连接的子节点a‘，若存在a‘,则p的fail指针就指向a‘，若不存在，则再找到a的fail指针所对应的b进行判断，一直找下去，直到找到-1（有可能字母x在tTrie树的其他位置根本没有出现过，所以没有次长后缀）。

以上过程均与KMP字符串匹配过程很相似。

所以现在我们就已经解决了fail指针构建的问题，接下来就是与文本串的匹配。

这也不难理解，还是仿照KMP字符串匹配过程，将文本串按照顺序放入Trie树，若发现当匹配到位置pos要求节点不存在，那么不断通过fail指针找到一个在Trie树种以pos为结尾的最长的后缀，然后继续进行匹配就行了，对于每到达一个节点，我们就可以在这个节点上搞事情，比如统计模式串出现位置，出现次数等等等等。

总结来说，AC自动机分为以下几个步骤：

1、读入所有模式串，在每个代表模式串的节点处记录信息。

2、按一定顺序构建每一个节点的fail指针。

3、匹配文本串，按题意处理信息。

 

下面附上AC自动机模板题，洛谷P3796，及其AC代码：

题目描述

有N个由小写字母组成的模式串以及一个文本串T。每个模式串可能会在文本串中出现多次。你需要找出哪些模式串在文本串T中出现的次数最多。

输入格式：

输入含多组数据。

每组数据的第一行为一个正整数N，表示共有N个模式串，1≤N≤150 。

接下去N行，每行一个长度小于等于70的模式串。下一行是一个长度小于等于10^6的文本串T。

输入结束标志为N=0。

输出格式：

对于每组数据，第一行输出模式串最多出现的次数，接下去若干行每行输出一个出现次数最多的模式串，按输入顺序排列。

 

AC代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<string>
#include<cmath>
#define LL long long
#define M 1000004
using namespace std;
int read(){
    int nm=0,fh=1;char cw=getchar();
    for(;!isdigit(cw);cw=getchar()) if(cw==‘-‘) fh=-fh;
    for(;isdigit(cw);cw=getchar()) nm=nm*10+(cw-‘0‘);
    return nm*fh;
}
int n,m,ans;
char ch[M],st[200][200];
struct stri{
    int tot,ord;
}sum[200];
struct ACA{
    int p[M][26],to[M],num[M],cnt;
    void init(){
        memset(to,0,sizeof(to));
        cnt=0,to[0]=-1;
        memset(p,-1,sizeof(p));
        memset(num,0,sizeof(num));
    }
    void add_letter(int x,int kd){p[x][kd]=++cnt;}
    void find(){
        for(int i=0;i<cnt;i++){
            for(int j=0;j<=25;j++){
                if(p[i][j]==-1) continue;
                if(i==0) to[p[i][j]]=0;
                else{
                    int k=to[i];
                    while(p[k][j]==-1&&k!=-1) k=to[k];
                    if(k==-1) k=0;
                    else k=p[k][j];
                    to[p[i][j]]=k;
                }
            }
        }
    }
    void insert(LL x){
        int tmp=0,m=strlen(st[x]);
        for(int i=0;i<m;i++){
            if(p[tmp][st[x][i]-‘a‘]==-1) add_letter(tmp,st[x][i]-‘a‘);
            tmp=p[tmp][st[x][i]-‘a‘];
        }
        num[tmp]=x;
    }
    void match(){
        m=strlen(ch);
        int now=0;
        for(int i=0;i<m;i++){
            if(p[now][ch[i]-‘a‘]==-1){
                now=to[now];
                while(now!=-1&&p[now][ch[i]-‘a‘]==-1) now=to[now];
                if(now==-1){now=0;continue;}
            }
            now=p[now][ch[i]-‘a‘];
            sum[num[now]].tot++;
            for(int k=to[now];k!=-1;k=to[k]) sum[num[k]].tot++;
        }
    }
}tr;
bool cmp(stri i,stri j){
    if(i.tot!=j.tot) return i.tot>j.tot;
    return i.ord<j.ord;
}
int main(){
    while(true){
        n=read();
        if(n==0) break;
        tr.init();
        for(int i=1;i<=n;i++){
            scanf("%s",st[i]);
            tr.insert(i);
            sum[i].tot=0,sum[i].ord=i;
        }
        tr.find();
        scanf("%s",ch),tr.match();
        
        sort(sum+1,sum+n+1,cmp);
        printf("%d\\n",sum[1].tot);
        for(int i=0;i<strlen(st[sum[1].ord]);i++) printf("%c",st[sum[1].ord][i]);
        puts("");
        for(int i=2;i<=n;i++){
            if(sum[i].tot<sum[i-1].tot) break;
            for(int j=0;j<strlen(st[sum[i].ord]);j++) printf("%c",st[sum[i].ord][j]);
            puts("");
        }
    }
    return 0;
}