[SinGuLaRiTy] NOIP2017 提高组
Posted SinGuLaRiTy2001
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[SinGuLaRiTy] NOIP2017 提高组相关的知识,希望对你有一定的参考价值。
【SinGuLaRiTy-1048】 Copyright (c) SinGuLaRiTy 2018. All Rights Reserved.
NOIP2017过了这么久,现在2018了才找到寒假这么一个空挡来写题解。哎,没办法,谁叫学校抓的紧呢。
序 | Before
这是我的最后一次NOIP。
因为是最后一次的原因吧,考前压力就蛮大的,再加上各种模拟赛,模板练习的轮番轰炸,走进考场时整个人都是“飘飘欲仙”的感觉~
我的NOIP2017就在这种“飘飘欲仙”的氛围下开始了。
游记 | Blogs
写游记是老规矩。
Day 1
T1 略略一瞟题目,我的妈,感觉是一个牛逼哄哄的数论题耶( •̀ ω •́ )y。磨了半天,最开始打表找规律,然后再画画数轴——咦?好像搞出来了些东西:ans=a*b-a-b?
嗯,就是这个样子的。
T2 看起来就很费时间,最后做......(1 hour later)不就是字符串的傻逼模拟题吗?就是模拟太TM复杂。(话说Day 1的字符串题我怎么没练过?)
剩下的时间都喂给T2了,考完了也没把判格式的那段调出来,直接报零。
T3 嗯,考前的模拟赛好像做过类似的(兴奋)。果断拓扑排序判0环,再加上DP。
考完后对答案:
“大佬,T3是不是拓扑排序判零环?”
“是的。”(淡定的回答)
“太好了欧耶!”
......
“你清数组了吗?”
“啥?要menset?”
GG......手动滑稽
Day 2
T1 紧张地看完题目,再瞟一眼数据范围......我的妈,这不就是dfs吗。10分钟码完。(今年做的最顺的一道题)
考完:“我为什么要脑抽加手残用一个sqrt?!”
T2 看起来就蛮复杂的——T3看起来好欺负一点。
被T3打回来:这玩意儿似乎是状压DP?
T3 嗯,这题怎么这么水?!——我的妈,这数据范围怎么这么恶心?O(M*N)都不让过?好吧,还是做做T2吧。
最后30分钟,又想了想,算了,还是打一个40分的暴力吧。
NOIP2017炸的飞起。总分340(为什么重庆作为竞赛弱“市”,一等线那么高?早知就去贵州了......)
题解 | Solution
D1T1 小凯的疑惑
【问题描述】
小凯手中有两种面值的金币,两种面值均为正整数且彼此互素。每种金币小凯都有无数个。在不找零的情况下,仅凭这两种金币,有些物品他是无法准确支付的。现在小凯想知道在无法准确支付的物品中,最贵的价值是多少金币?注意:输入数据保证存在小凯无法准确支付的商品。
【输入格式】
输入文件名为 math.in。
输入数据仅一行,包含两个正整数 a 和 b,它们之间用一个空格隔开,表示小凯手中金币的面值。
【输出格式】
输出文件名为 math.out。
输出文件仅一行,一个正整数 N,表示不找零的情况下,小凯用手中的金币不能准确支付的最贵的物品的价值。
【数据规模与约定】
对于 30%的数据: 1 ≤ a,b ≤ 50。
对于 60%的数据: 1 ≤ a,b ≤ 10,000。
对于 100%的数据:1 ≤ a,b ≤ 1,000,000,000。
【题解】
找规律吧,没什么可以说的。
#include<cstdio> #include<iostream> using namespace std; long long a,b; int main() { cin>>a>>b; cout<<a*b-a-b; return 0; }
D1T2 时间复杂度
【问题描述】
小明正在学习一种新的编程语言 A++,刚学会循环语句的他激动地写了好多程序并给出了他自己算出的时间复杂度,可他的编程老师实在不想一个一个检查小明的程序,于是你的机会来啦!下面请你编写程序来判断小明对他的每个程序给出的时间复杂度是否正确。
A++语言的循环结构如下:

其中“F i x y”表示新建变量 (i 变量 i 不可与未被销毁的变量重名)并初始化为 x,然后判断 i 和 y 的大小关系,若 i 小于等于 y 则进入循环,否则不进入。每次循环结束后i都会被修改成i +1,一旦i 大于 y 终止循环。
x和 y 可以是正整数(x 和 y 的大小关系不定)或变量 n。n 是一个表示数据规模的变量,在时间复杂度计算中需保留该变量而不能将其视为常数,该数远大于 100。
“E”表示循环体结束。循环体结束时,这个循环体新建的变量也被销毁。
注:本题中为了书写方便,在描述复杂度时,使用大写英文字母“O”表示通常意义下“Θ”的概念。
【输入格式】
输入文件名为 complexity.in。
输入文件第一行一个正整数 t,表示有 t(t ≤ 10)个程序需要计算时间复杂度。每个程序我们只需抽取其中 “F i x y”和“E”即可计算时间复杂度。注意:循环结构允许嵌套。
接下来每个程序的第一行包含一个正整数 L 和一个字符串,L 代表程序行数,字符串表示这个程序的复杂度,“O(1)”表示常数复杂度,“O(n^w)”表示复杂度为n^w,其中 w 是一个小于 100 的正整数(输入中不包含引号),输入保证复杂度只有 O(1)和 O(n^w) 两种类型。
接下来 L 行代表程序中循环结构中的“F i x y”或者 “E”。
程序行若以“F”开头,表示进入一个循环,之后有空格分离的三个字符(串)i x y,其中 i 是一个小写字母(保证不为“n”),表示新建的变量名,x 和 y 可能是正整数或 n ,已知若为正整数则一定小于 100。
程序行若以“E”开头,则表示循环体结束。
【输出格式】
输出文件名为 complexity.out。
输出文件共 t 行,对应输入的 t 个程序,每行输出“Yes”或“No”或者“ERR”(输出中不包含引号),若程序实际复杂度与输入给出的复杂度一致则输出“Yes”,不一致则输出“No”,若程序有语法错误(其中语法错误只有: F 和E 不匹配;新建的变量与已经存在但未被销毁的变量重复两种情况),则输出“ERR”。
注意:即使在程序不会执行的循环体中出现了语法错误也会编译错误,要输出 “ERR”。
【数据规模与约定】
对于 30%的数据:不存在语法错误,数据保证小明给出的每个程序的前 L/2 行一定为以 F 开头的语句,第L/2+1 行至第 L 行一定为以 E 开头的语句,L<=10,若 x、y 均为整数,x 一定小于 y,且只有 y 有可能为 n。
对于50%的数据:不存在语法错误,L<=100,且若x、y均为整数,x 一定小于 y,且只有 y 有可能为 n。
对于 70%的数据:不存在语法错误,L<=100。
对于 100%的数据:L<=100。
【题解】
用STL stack进行模拟,话说这代码量在历届NOIP的模拟中居然还算短的?!
#include<cstring> #include<stack> #include<cmath> #include<cstdio> #include<iostream> #include<algorithm> #include<cstdlib> using namespace std; int t,hang,zhishu,wuxiao=0,ans,qzhishu; struct chuan { char bianliang; int zhishu_changshu;//0无效 1指数 2常数 } aaa; stack<chuan>q; bool changshu,shiyong[10000],flag; char fuzadu[100],kaishi[100],jieshu[100]; void xvnhuan() { cin>>aaa.bianliang>>kaishi>>jieshu; if(!shiyong[int(aaa.bianliang)])shiyong[int(aaa.bianliang)]=1;//是否销毁 else { if(!flag)printf("ERR\\n"); flag=1; } if(kaishi[0]==jieshu[0]&&jieshu[0]==\'n\') { q.push((chuan) { aaa.bianliang,2 }); return ; } int lena=strlen(kaishi),shua=0; int lenb=strlen(jieshu),shub=0; for(int i=0; i<lena; i++) //第一个串 { if(kaishi[i]!=\'n\') { shua*=10; shua+=(int(kaishi[i])-48); } else { q.push((chuan) { aaa.bianliang,0 }); wuxiao++;//无效。 return ; } } for(int i=0; i<lenb; i++) //第二个串 { if(jieshu[i]!=\'n\') { shub*=10; shub+=(int(jieshu[i])-48); } else if(jieshu[i]==\'n\') { q.push((chuan) { aaa.bianliang,1 }); if(!wuxiao) { qzhishu++; ans=max(ans,qzhishu); } return; } } if(shua<=shub)q.push((chuan) { aaa.bianliang,2 }); else { q.push((chuan) { aaa.bianliang,0 }); wuxiao++; }//无效 } void mem() { qzhishu=0; ans=0; wuxiao=0; flag=0; changshu=0; zhishu=0; memset(fuzadu,0,sizeof(fuzadu)); memset(shiyong,0,sizeof(shiyong)); while(!q.empty())q.pop(); } void Print() { if(!flag) { if(!q.empty()) { printf("ERR\\n"); return; } if(changshu) { if(!ans)printf("Yes\\n"); else printf("No\\n"); return ; } else if(!changshu) { if(ans==zhishu)printf("Yes\\n"); else printf("No\\n"); return ; } } } int main() { scanf("%d",&t); for(int ll=1; ll<=t; ll++) { mem(); scanf("%d%s",&hang,fuzadu); int changdu=strlen(fuzadu); if(fuzadu[2]==\'1\') { changshu=1; } else { for(int i=4; i<changdu-1; i++) { zhishu*=10; zhishu=zhishu+int(fuzadu[i])-48; } } for(int i=1; i<=hang; i++) { char leixing; scanf("%s",&leixing); if(leixing==\'F\')xvnhuan(); else { if(q.empty()) { if(!flag)printf("ERR\\n"); flag=1; } else { chuan aaaa=q.top(); q.pop(); shiyong[int(aaaa.bianliang)]=0; if(aaaa.zhishu_changshu==0)wuxiao--; if(aaaa.zhishu_changshu==1&&wuxiao==0)qzhishu--; } } } Print(); } return 0; }
D1T3 逛公园
【问题描述】
策策同学特别喜欢逛公园。公园可以看成一张N个点M条边构成的有向图,且没有自环和重边。其中1号点是公园的入口,N号点是公园的出口,每条边有一个非负权值,代表策策经过这条边所要花的时间。
策策每天都会去逛公园,他总是从1号点进去,从N号点出来。
策策喜欢新鲜的事物,他不希望有两天逛公园的路线完全一样,同时策策还是一个特别热爱学习的好孩子,他不希望每天在逛公园这件事上花费太多的时间。如果1号点到N号点的最短路长为d,那么策策只会喜欢长度不超过d+K的路线。
策策同学想知道总共有多少条满足条件的路线,你能帮帮他吗?
为避免输出过大,答案对P取模。
如果有无穷多条合法的路线,请输出−1。
【输入格式】
输入文件名为 park.in。
第一行包含一个整数T, 代表数据组数。
接下来T组数据,对于每组数据:
第一行包含四个整数N, M, K, P,每两个整数之间用一个空格隔开。
接下来M行,每行三个整数ai , bi , ci,代表编号为ai, bi的点之间有一条权值为ci的有向边,每两个整数之间用一个空格隔开。
【输出格式】
输出文件名为 park.out。
输出文件包含T行,每行一个整数代表答案。
【数据规模与约定】
对于不同的测试点,我们约定各种参数的规模不会超过如下:
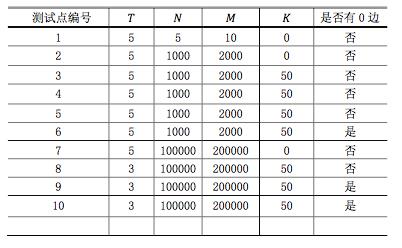
对于100%的数据, 1≤P≤109,1≤ai,bi≤
以上是关于[SinGuLaRiTy] NOIP2017 提高组的主要内容,如果未能解决你的问题,请参考以下文章