一、性质
①节点是红色或者黑色。
②根节点是黑色。
③叶节点(NIL)是黑色。
④红色节点的孩子是黑色。
⑤从任意节点到叶节点的路径包含相同数量的黑色节点。
注:红黑树的叶节点为空节点。
二、操作
①左旋
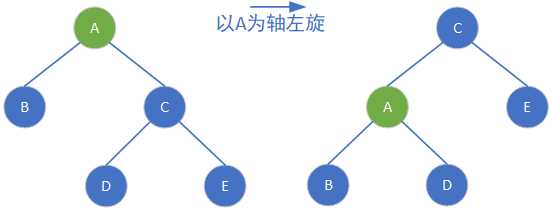
②右旋
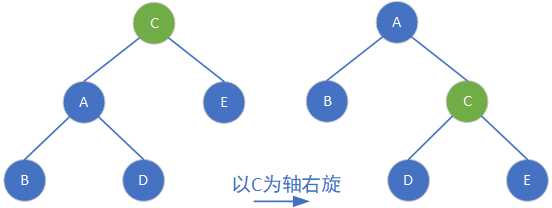
三、插入
将红黑树作为普通的二叉搜索树进行插入,插入节点默认涂为红色。
插入情况如下:
①若当前节点大于插入节点,且没有左子节点,将插入节点作为当前节点的左子节点插入。否则当前节点变成其左子节点。
②若当前节点小于插入节点,且没有右子节点,将插入节点作为当前节点的右子节点插入。否则当前节点变成其右子节点。
③若当前节点等于插入节点,则插入失败。
插入后调整情况如下:(当前节点初始为插入节点)
①若当前节点的父亲节点为黑色,则红黑树性质仍然保持。
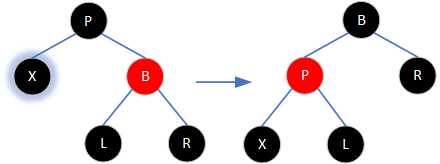
②若当前节点的父亲节点为红色、叔叔节点为黑色,则将父亲节点涂为黑色,祖父节点涂为红色。以祖父节点为轴进行右旋,至此红黑树性质恢复。
③若当前节点的父亲节点和叔叔节点均为红色,则将父亲节点和叔叔节点涂为黑色,祖父节点涂为红色。以祖父节点作为当前节点继续回溯。
四、删除
将红黑树作为普通的二叉搜索树进行删除。
删除情况如下:
①若删除节点没有子节点,则直接删除。
②若删除节点有一个子节点,则直接删除后其子节点代替其位置。
③若删除节点有两个子节点,则将其与子节点交换直到出现①或②。
删除后调整情况如下:
①若删除节点为红色,则红黑树性质仍然保持。
②若删除节点为黑色,且仅有一个子节点,那么该子节点必为红色。删除完成后将该替代删除节点的子节点涂为黑色即可恢复红黑树性质。
③若删除节点为黑色,且子节点均为NIL,那么存在情况如下:(当前节点初始为NIL节点,绿色表示任意颜色)
㈠若当前节点的兄弟节点为黑色,且存在红色侄子节点。
⑴若当前节点为右子节点,左侄子节点为红色。则将兄弟节点涂为父节点的颜色、左侄子节点和父节点涂为黑色,然后以父节点为轴进行一次右旋即可恢复红黑树性质。
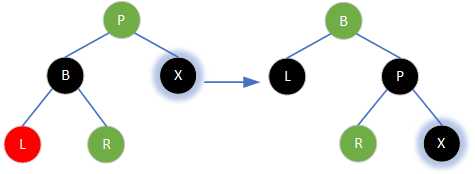
⑵若当前节点为右子节点,左侄子节点为黑色,右侄子节点为红色。则先将右侄子节点涂为父节点的颜色、父节点涂为黑色,然后以兄弟节点为轴进行一次左旋,最后以父节点为轴进行一次右旋即可恢复红黑树性质。
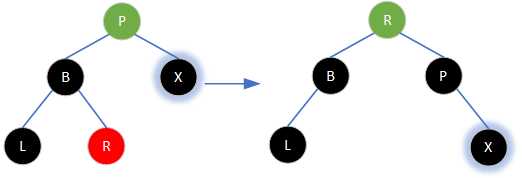
⑶若当前节点为左子节点,右侄子节点为红色。则将兄弟节点涂为父节点的颜色、右侄子节点和父节点涂为黑色,然后以父节点为轴进行一次左旋即可恢复红黑树性质。
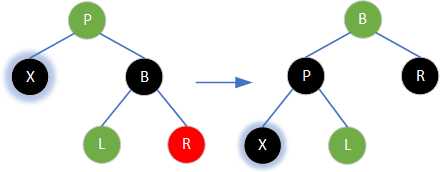
⑷若当前节点为左子节点,右侄子节点为黑色,左侄子节点为红色。则先将左侄子节点涂为父节点的颜色、父节点涂为黑色,然后以兄弟节点为轴进行一次右旋,最后以父节点为轴进行一次左旋即可恢复红黑树性质。

㈡若当前节点的兄弟节点和侄子节点均为黑色,父节点为红色。则将父节点涂为黑色,兄弟节点涂为红色即可恢复红黑树性质。
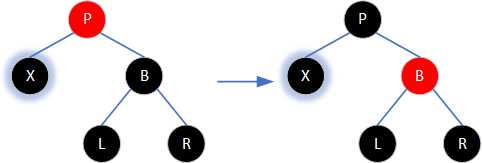
㈢若当前节点的兄弟节点、侄子节点和父节点均为黑色。则将兄弟节点涂为红色,将父节点作为新的当前节点继续回溯。
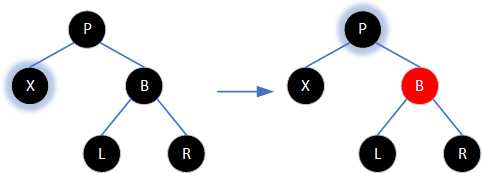
㈣若当前节点的兄弟节点为红色。则将兄弟节点涂为黑色,父节点涂为红色,以父节点为轴进行一次旋转(当前节点为左子节点则左旋,为右子节点则右旋)后继续回溯。