吴恩达“机器学习”——学习笔记五

Posted 2020-10-22 辛侠平

朴素贝叶斯算法(Naive Bayes)(续学习笔记四)

两个朴素贝叶斯的变化版本

x_i可以取多个值，即p(x_i｜y)是符合多项式分布的，不是符合伯努利分布的。其他的与符合伯努利的情况一样。(同时也提供一种思路将连续型变量变成离散型的，比如说房间的面积可以进行离散分类，然后运用这个朴素贝叶斯算法的变形)。

第二个朴素贝叶斯的变化形式专门用来处理文本文档，即对序列进行分类，被称为朴素贝叶斯的事件模型(event model)。这将使用一种不同的方式将邮件转化为特征向量。

之前的特征向量是：向量维度是字典的大小，此向量将会把邮件中出现的单词在字典中标记为1，未出现的单词标记为0。

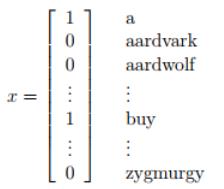
现在将特征向量进行变化：向量维度是邮件的长度，向量中的每一个元素对应用邮件中的对应位置的单词。加入邮件是‘a nips’。假如a在字典中的位置是第一位，nips在字典中的位置是3500位。那么x_0=1,x_1=3500。对应的生成模型就变成了，n代表邮件单词的数量，xi服从多项式分布。对应的参数为φy = p(y)，φi|y=1 = p(x_ j = i|y = 1) (for any j)，φi|y=0 = p(x_ j = i|y = 0)。给出训练集合，可以求得参数的最大似然估计：

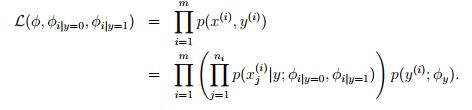
根据laplace平滑，可以得到，

神经网络(neural network)

可以生成非线性分类器。（生成学习算法中的高斯判别和朴素贝叶斯都是和logistics函数相关的线性分类器）

将特征先传递到中间层的sigmoid单元，在将中间层的sigmoid单元传递到输出层的sigmoid单元中。

对应的函数以及成本可以写成：

 

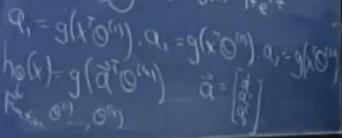
在神经网络中使用梯度下降算法，称为反向传播。

支持向量机(support vector machine)

另外一种可以生成非线性分类器的算法。

先进行线性分类器的说明。

考虑logistics回归，使用的是sigmoid函数，h>0.5时，我们就认为y为1，或者说，theta^T(x)>0时，我们就认为y为1。所以，如果theta^T(x)远大于0，我们就可以坚信y=1，如果theta^T(x)远小于0，我们就可以坚信y=0。这可以从sigmo图像中很容易得到。可以根据theta^T(x)=0，来找出一条边界线，距离这条边界线越远，我们就对它的预测值更有信心，离这条线越近，我们对它的预测值的信心就会减少。

在SVM中，改变了一些约束：y的取值变成了-1和1，不再是0与1了；预测值的参数也变成了w和b了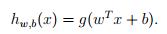g也不再是sigmoid函数了，而是g(z) = 1 if z ≥ 0, and g(z) = −1 otherwise。

w^Tx+b与之前的θ^Tx本质上是一样的，只不过之前假设的是x_0等于1。w=[θ1 . . . θn] ^T,b=θ0。

函数间隔

给定训练样本，我们定义函数间隔为

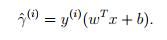如果y^(i)=1,为了让预测更加正确，应该要求w^Tx+b为一个很大的正数，如果y^(i)=-1，我们应该要求w^Tx+b为一个很小的负数。我们认为y^ (i) (w T x + b) > 0，那么我们的预测就是正确的。

如果有多个训练样本，就定义

即离分界线最近的一种情况，即最坏的情况。现在就转化为在最坏的情况下，使得函数间隔最大。但是，如果使得w和b同时加倍，此时的边界线不变，但是函数间隔会随着w和b的加倍而加倍，但是这种大的函数间隔是没什么用的。所以可以进行正规化处理解决这个问题。

几何间隔

A(x^(i),y^(i)),w是分界线的法向量，gamma是A与B之间的距离。那么B点就有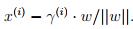同时B点存在所以可以得到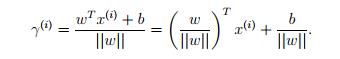更一般的，我们可以写成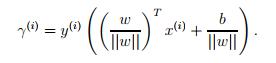所以，几何间距是一个化归处理的函数间距。当有多个样本时，我们也定义

最大间隔分类器

SVM的前身

即选择gamma,w,b使得几何间隔最大（在满足 y (i) (w T x (i) + b) ≥ γ, i = 1, . . . , m ||w|| = 1.的条件下）。