腾讯编程题

Posted 2020-10-22 zhchoutai

这是一个腾讯笔试的编程题：

我们经常会用到一个LCS的问题。本题的唯一的一个巧妙之处在于。最后求解的字符串变为的是原来的字符串与其reverse之后的字符串的最大LCS，这样本题就得到了解决。

最长公共子序列求解：递归与动态规划方法

　　在做OJ题目的时候。常常会用到字符串的处理。比如。比較二个字符串相似度。

这篇文章介绍一下求两个字符串的最长公共子序列。

　　一个字符串的子序列。是指从该字符串中去掉随意多个字符后剩下的字符在不改变顺序的情况下组成的新字符串。

　　最长公共子序列。是指多个字符串可具有的长度最大的公共的子序列。

　　(1)递归方法求最长公共子序列的长度

　　　　1)设有字符串a[0...n]。b[0...m]，以下就是递推公式。

             当数组a和b相应位置字符同样时。则直接求解下一个位置；当不同一时候取两种情况中的较大数值。

　　　　

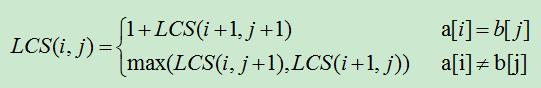
　　　　2)代码例如以下：

#include<stdio.h>
#include<string.h>
char a[30],b[30];
int lena,lenb;
int LCS(int,int);　　///两个參数分别表示数组a的下标和数组b的下标

int main()
{
    strcpy(a,"ABCBDAB");
    strcpy(b,"BDCABA");
    lena=strlen(a);
    lenb=strlen(b);
    printf("%d\\n",LCS(0,0));
    return 0;
}

int LCS(int i,int j)
{
    if(i>=lena || j>=lenb)
        return 0;
    if(a[i]==b[j])
        return 1+LCS(i+1,j+1);
    else
        return LCS(i+1,j)>LCS(i,j+1)? LCS(i+1,j):LCS(i,j+1);
}

 　　　　用递归的方法长处是编程简单，easy理解。缺点是效率不高，有大量的反复运行递归调用，并且仅仅能求出最大公共子序列的长度，求不出详细的最大公共子序列。

　　(2)动态规划求最长公共子序列的长度

　　　　动态规划採用二维数组来标识中间计算结果。避免反复的计算来提高效率。

　　　　1)最长公共子序列的长度的动态规划方程

　　　　设有字符串a[0...n]，b[0...m]，以下就是递推公式。字符串a相应的是二维数组num的行，字符串b相应的是二维数组num的列。

　　　　

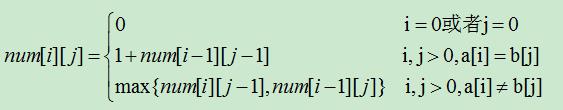
　　　　另外，採用二维数组flag来记录下标i和j的走向。数字"1"表示，斜向下；数字"2"表示。水平向右。数字"3"表示，竖直向下。这样便于以后的求解最长公共子序列。

　　　　(2)求解公共子序列代码

#include<stdio.h>
#include<string.h>

char a[500],b[500];
char num[501][501]; ///记录中间结果的数组
char flag[501][501];    ///标记数组，用于标识下标的走向。构造出公共子序列
void LCS(); ///动态规划求解
void getLCS();    ///採用倒推方式求最长公共子序列

int main()
{
    int i;
    strcpy(a,"ABCBDAB");
    strcpy(b,"BDCABA");
    memset(num,0,sizeof(num));
    memset(flag,0,sizeof(flag));
    LCS();
    printf("%d\\n",num[strlen(a)][strlen(b)]);
    getLCS();
    return 0;
}

void LCS()
{
    int i,j;
    for(i=1;i<=strlen(a);i++)
    {
        for(j=1;j<=strlen(b);j++)
        {
            if(a[i-1]==b[j-1])   ///注意这里的下标是i-1与j-1
            {
                num[i][j]=num[i-1][j-1]+1;
                flag[i][j]=1;  ///斜向下标记
            }
            else if(num[i][j-1]>num[i-1][j])
            {
                num[i][j]=num[i][j-1];
                flag[i][j]=2;  ///向右标记
            }
            else
            {
                num[i][j]=num[i-1][j];
                flag[i][j]=3;  ///向下标记
            }
        }
    }
}

void getLCS()
{

    char res[500];
    int i=strlen(a);
    int j=strlen(b);
    int k=0;    ///用于保存结果的数组标志位
    while(i>0 && j>0)
    {
        if(flag[i][j]==1)   ///假设是斜向下标记
        {
            res[k]=a[i-1];
            k++;
            i--;
            j--;
        }
        else if(flag[i][j]==2)  ///假设是斜向右标记
            j--;
        else if(flag[i][j]==3)  ///假设是斜向下标记
            i--;
    }

    for(i=k-1;i>=0;i--)
        printf("%c",res[i]);
}

　　　　(3)图示

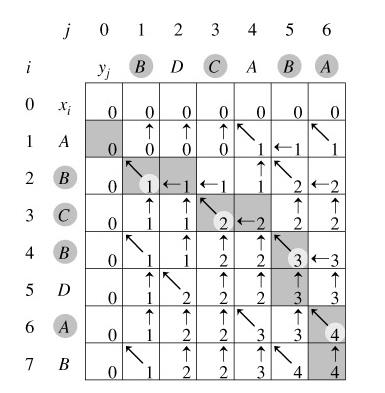
也可採用递归的方式。缺点在于仅仅能得到最长公共子数列的长度，而无法得到详细的子字符串：

#include<stdio.h>
#include<string.h>
char a[30],b[30];
int lena,lenb;
int LCS(int,int);　　///两个參数分别表示数组a的下标和数组b的下标

int main()
{
    strcpy(a,"ABCBDAB");
    strcpy(b,"BDCABA");
    lena=strlen(a);
    lenb=strlen(b);
    printf("%d\\n",LCS(0,0));
    return 0;
}

int LCS(int i,int j)
{
    if(i>=lena || j>=lenb)
        return 0;
    if(a[i]==b[j])
        return 1+LCS(i+1,j+1);
    else
        return LCS(i+1,j)>LCS(i,j+1)?
 LCS(i+1,j):LCS(i,j+1);
}