题目
给出n个数qi,给出Fj的定义如下:
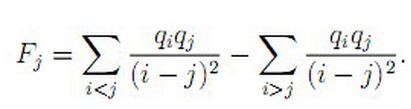
令Ei=Fi/qi,求Ei.
输入格式
第一行一个整数n。
接下来n行每行输入一个数,第i行表示qi。
输出格式
n行,第i行输出Ei。与标准答案误差不超过1e-2即可。
输入样例
5
4006373.885184
15375036.435759
1717456.469144
8514941.004912
1410681.345880
输出样例
-16838672.693
3439.793
7509018.566
4595686.886
10903040.872
题解
卷积什么的感觉好优美~~
卷积
先普及一下离散卷积的定义【瞎编的】:
对于两个序列\\(x(n)\\)和\\(y(n)\\)
其卷积\\((x*y)(n) = \\sum_{-\\infty}^{\\infty}x(k)y(n - k)\\)
即当一个序列所有i位置上的值c(i)等于所有位置之和为i的x(k)*y(i - k)乘积的和时,可以看做c()为x()和y()的卷积
就好比多项式a(n) b(n)相乘,对于次数i的系数\\(c(i)=\\sum a(k)*b(i - k)\\)
而求离散卷积可以使用离散快速傅里叶\\(O(nlogn)\\)高效求出
本题##
观察式子
\\(Ei = \\sum_{j<i}\\frac{qj}{(i-j)^2} - \\sum_{j>i}\\frac{qj}{(i-j)^2}\\)
我们将两个求和分开来求
我们令\\(b(i) = \\frac{1}{i^2}\\),特别的,\\(b(0) = 0\\)
我们令\\(a(i) = qi\\)
我们会发现左边【即为\\(L(i)\\)】\\(L(i) = \\sum a(j)*b(i - j)\\),刚好就是卷积的形式
可以用fft求出
同样的,对于右边
\\(R(i) = \\sum a(j)*b(j - i)\\)
诶?不对啊,\\(j + j - i\\)不是定值啊。
但是ta们的位置关系还是很固定,考虑变形
我们将\\(a(i)\\)翻转,即令\\(c(n-i)=a(i)\\)
奇迹发生了:
\\(R(i) = \\sum c(n - j)*b(j - i)\\)
这样我们算出的卷积,\\(R(i)\\)就与\\(E_{n-i}\\)对应
最后将算出的两个结果相减
呼啦啦,搞完啦~~
#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<complex>
#include<algorithm>
#define LL long long int
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<\' \'; puts("");
using namespace std;
const int maxn = 400005,maxm = 100005,INF = 1000000000;
const double pi = acos(-1);
typedef complex<double> E;
E a[maxn],b[maxn],aa[maxn];
int n,m,L,R[maxn];
void fft(E* a,int f){
for (int i = 0; i < n; i++) if (i < R[i]) swap(a[i],a[R[i]]);
for (int i = 1; i < n; i <<= 1){
E wn(cos(pi / i),f * sin(pi / i));
for (int j = 0; j < n; j += (i << 1)){
E w(1,0);
for (int k = 0; k < i; k++,w *= wn){
E x = a[j + k],y = w * a[j + k + i];
a[j + k] = x + y; a[j + k + i] = x - y;
}
}
}
if (f == -1) for (int i = 0; i < n; i++) a[i] /= n;
}
int main(){
scanf("%d",&n); --n; double q;
for (int i = 0; i <= n; i++){
scanf("%lf",&q);
a[i] = q; aa[n - i] = q;
}
for (int i = 1; i <= n; i++) b[i] = 1.0 / i / i;
m = n << 1; for (n = 1; n <= m; n <<= 1) L++;
for (int i = 0; i < n; i++) R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1));
fft(a,1); fft(aa,1); fft(b,1);
for (int i = 0; i < n; i++) a[i] *= b[i];
for (int i = 0; i < n; i++) aa[i] *= b[i];
fft(a,-1); fft(aa,-1);
for (int i = 0; i <= (m >> 1); i++) printf("%.6lf\\n",a[i].real() - aa[(m >> 1) - i].real());
return 0;
}