POJ - 3111 K Best （二分查找）

Posted 2020-10-22 ecliwalker

 

一、题目概述 K Best Time Limit: 8000MS   Memory Limit: 65536K Total Submissions: 12167   Accepted: 3126 Case Time Limit: 2000MS   Special Judge Description Demy has n jewels. Each of her jewels has some value vi and weight wi. Since her husband John got broke after recent financial crises, Demy has decided to sell some jewels. She has decided that she would keep k best jewels for herself. She decided to keep such jewels that their specific value is as large as possible. That is, denote the specific value of some set of jewels S = {i1, i2, …, ik} as . Demy would like to select such k jewels that their specific value is maximal possible. Help her to do so. Input The first line of the input file contains n — the number of jewels Demy got, and k — the number of jewels she would like to keep (1 ≤ k ≤ n ≤ 100 000). The following n lines contain two integer numbers each — vi and wi (0 ≤ vi ≤ 106, 1 ≤ wi ≤ 106, both the sum of all vi and the sum of all wi do not exceed 107). Output Output k numbers — the numbers of jewels Demy must keep. If there are several solutions, output any one. Sample Input 3 2 1 1 1 2 1 3 Sample Output 1 2 Source Northeastern Europe 2005, Northern Subregion

[Submit]   [Go Back]   [Status]   [Discuss]

二、题目释义

有N颗珠宝，每颗珠宝的价值为vi，重量为wi。 女主不得已要卖掉部分珠宝，她想留下k颗珠宝，并要求(v1+v2+....vk) / (w1+w2+...wk)的值最大，输出女主留下的珠宝的编号。（可不按输入的顺序输出）。

三、思路分析

四、AC代码

 

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 1e5+5;
const double esp = 1e-6;

struct jewel
{
    double v,w,t;
    int id;
}S[N];
int n,k;
bool cmp(jewel a, jewel b)
{
    return a.t > b.t;
}

bool check(double x)
{
    double sum = 0;
    for(int i=0; i<n; i++)
    {
        S[i].t = S[i].v - x*S[i].w;
    }
    sort(S,S+n,cmp);
    for(int i=0; i<k; i++)
    {
        sum += S[i].t;
    }
    return sum >= 0;
}

int main()
{
    double l,r;
    double mid;

    while(scanf("%d%d",&n,&k) != EOF)
    {
        r = 0;
        for(int i=0; i<n; i++)
        {
            scanf("%lf%lf",&S[i].v,&S[i].w);
            S[i].id = i+1;
            r = max(r,S[i].v / S[i].w);
        }
        while(r-l>esp)
        {
            mid = (l+r) / 2;
            if(check(mid)) l = mid;
            else r = mid;
        }
        for(int i=0; i<k-1; i++)
        {
            cout << S[i].id << " ";
        }
        cout << S[k-1].id << endl;
    }
    return 0;
}
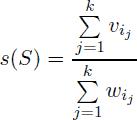