吴恩达“机器学习”——学习笔记二

Posted 2020-10-22 辛侠平

定义一些名词

欠拟合（underfitting）：数据中的某些成分未被捕获到，比如拟合结果是二次函数，结果才只拟合出了一次函数。

过拟合（overfitting）：使用过量的特征集合，使模型过于复杂。

参数学习算法（parametric learning algorithms）：用固定的参数进行数据的拟合。比如线性回归。

非参数学习算法（non-parametric learning algorithms）：使用的参数随着训练样本的增多而增多。

局部加权回归（locally weighted regression）

一种非参数学习算法。

算法思想：寻找到theta，使得

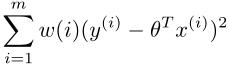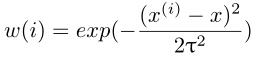, 最小，其中w(i)称为权值，tau称为波长参数。由公式可知，我们在进行局部加权回归时，对离x较近的训练样本赋予了较大的权重，对离x远的样本赋予了较小的权重。可以这样说，我们在对某一个x进行局部加权回归时，只使用x周围的数据。

对线性模型的概率解释

解释为何要在线性回归中选择最小二乘法

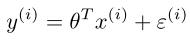，其中varepsilon为误差项（error），假设该误差项服从均值为0，方差为sigma的正态分布，且varepsilon是IID，即独立同分布的。

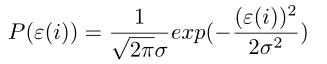，将y用varepsilon换掉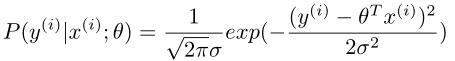，则

 

，则

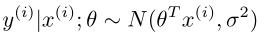
定义似然函数为

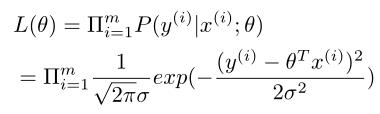
求出最大似然估计即可

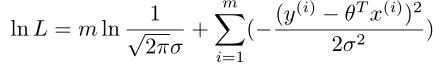
即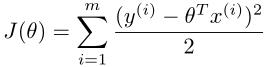最小，此处隐含sigma对我们的运算无影响。

 

所以最小二乘法的目的实际上是假设误差项满足高斯分布且独立同分布的条件下使似然性最大化。

第一个分类算法

可以采用线性回归解决分类问题，但是有时候结果是好的，有时候结果是糟糕的，一般不这样做。

讨论二元分类，即y只能取0和1。那么我们的h，即预测值可以假定在0与1之间。所以可以选择logistic（sigmoid）函数来表示我们的h。即

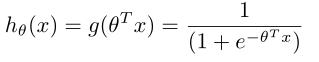
对分类算法模型的概率解释

假设我们估计的是y=1的时候的概率，那么

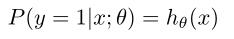
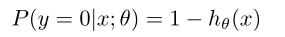我们可以将两个式子写在一块

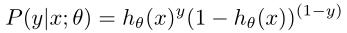
同样进行最大似然估计

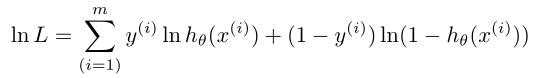
可以用梯度上升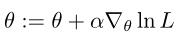

 

算法进行最大似然估计

 

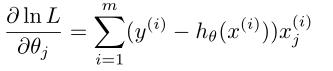
那么学习过程就变成了

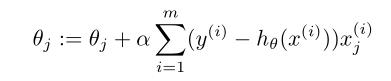
这与在线性回归中使成本函数J最小的学习过程一样！！！

感知器算法（perceptron algorithm）

感知器算法不是使用logistics函数，而是使用以下函数

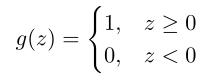
同样可以得到相同的学习过程。