算法导论笔记第6章 堆和堆排序

Posted 2020-10-22 jackson-zhou

堆排序结合了插入排序和归并排序的有点：它空间复杂度是O(1), 时间复杂度是O(nlgn).

要讲堆排序，先讲数据结构“堆”

堆：

　　堆是用数组来存放一个完全二叉树的数据结构。假设数组名是A，树的根节点存放在A[1]。它的左孩子存放在A[2]，右孩子存放在A[3]

　　即：对于某个下标位i的节点，它的左孩子是A[2i],  右孩子是A[2i+1].  父节点是A[i/2]

PARENT(i)
   return ?i/2?

LEFT(i)
   return 2i

RIGHT(i)
   return 2i + 1


这个结论很简单也很好记忆，只是有一个小问题：算法导论的数组下标是从1开始的。而现实中大部分流行语言的数组下标却是从0开始的。这里有一个小技巧是将A[0]元素保留不使用，就可以规避掉这个问题。

不过在C++的标准库STL，或者是Golang的container/heap/heap.go里，并没有使用这个小技巧。
公式调整为

PARENT(i)
   return ?(i-1）/2?

LEFT(i)
   return 2i + 1

RIGHT(i)
   return 2i + 2

不建议记这个公式，会造成混乱。只需要知道有这么一回事就行。

堆有两个应用：

1. 堆排序时使用的是最大堆。
   
2. 优先级队列使用的是最小堆。

  堆的基本函数有：

   max_heapify。它是保持最大堆性质的关键函数。运行时间是o(lgn);

 

   build_max_heap 以线性时间运行，可以在无序的输入数组基础上构建出最大堆

   heapsort 运行时间是O(nlgn), 可以对一个数组进行原地排序。

   max_heap_insert, heap_extract_max, heap_increase_key和heap_maximum运行时间为O(lgn),可以让堆结构作为优先队列使用。

书上递归版本的max_heapify

#define PARENT(i) ((i)/2)
#define LEFT(i) (2*(i))
#define RIGHT(i) (2*(i)+1)
void max_heapify(int* A, int heap_size, int i) {
  int l = LEFT(i);
  int r = RIGHT(i);
  int largest = 0;
  if ((l < heap_size) && (A[l] > A[i])) {
    largest = l;
  }else {
    largest = i;
  }

  if ((r < heap_size) && A[r] > (A[largest])) {
    largest = r;
  }

  if (largest != i) {
    int temp = A[i];
    A[i] = A[largest];
    A[largest] = temp;
    max_heapify(A,heap_size,largest);
  }
}

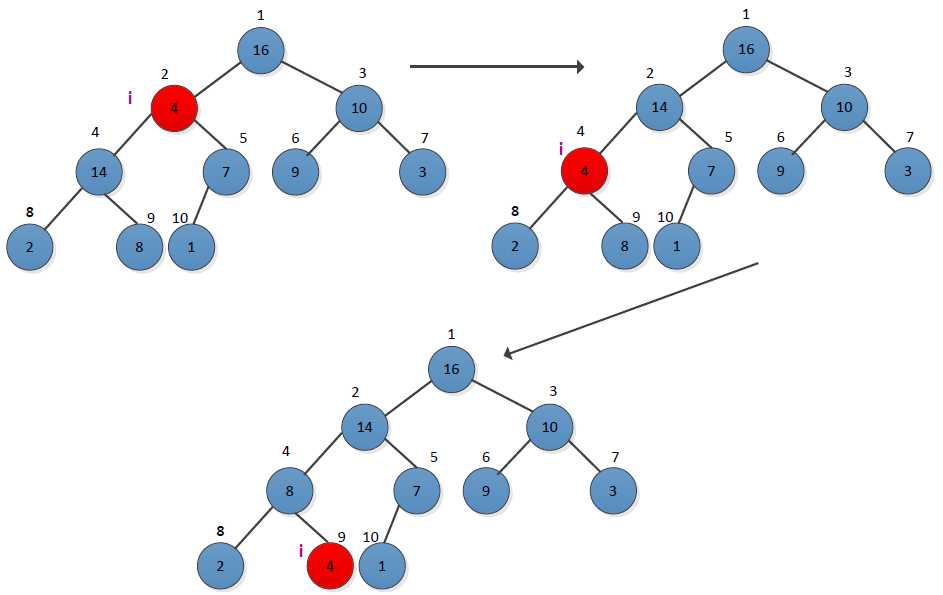
在算法的每一步里，从元素A[i], A[LEFT(i)], A[RIGHT(i)]中找出最大的。并将其下标存放在largest中。如果A[i]是最大的，则以为跟的子树已经是最大堆，程序结束。

否则i的某个子节点中有最大元素，则交换 A[i]和A[largest]，从而使i及其子女满足堆性质。下标largest的节点在交换后的值是A[i],以该节点为根的字数又有可能违反最大堆性质，因此要对子树递归调用max_heapify。递归调用的次数是树的高度。而完全二叉树的高度是lgn, 所以该算法的时间复杂度是O(lgn)

 

 

void build_max_heap(int *A, int heap_size) {
  int i;
  for (i = heap_size / 2; i >0; i ++) {
    max_heapify(A, heap_size, i);
  }
}

 

为了证明算法是正确的，我们用循环不变式来分析一下： 循环中不变的量是每一次迭代开始时，节点i+1, i+2,...,n都是一个最大堆的根。

1. 初始化：在第一轮循环迭代之前，i=(n/2)。 节点(n/2)+1, (n/2) + 2...,n都是叶节点，也是平凡最大堆的根。
2. 保持：节点i的子节点的编号均比i大。于是根据循环不变式这些子节点都是最大堆的根。着也是调用函数max_heapify以是节点i成为最大堆的根的前提条件。此外，max_heapify的调用保持了节点i+1,i+2，。。。。。n成为最大堆的根的性质。在循环中递减，记为下一次迭代重新建立了循环不变式。
3. 终止：过程终止时，i=0根据循环不变式，我们知道节点1,2,...n中，每个都是最大堆的根，节点1就是一个最大堆的根。