经典算法二叉树 & 平衡二叉树 & 红黑树
Posted 人生如逆旅,我亦是行人。
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了经典算法二叉树 & 平衡二叉树 & 红黑树相关的知识,希望对你有一定的参考价值。
参考文档:
avl树:http://lib.csdn.net/article/datastructure/9204
avl树:http://blog.csdn.net/javazejian/article/details/53892797
trie树:https://www.cnblogs.com/huangxincheng/archive/2012/11/25/2788268.html
b,b+,b* 树 :https://www.cnblogs.com/wjoyxt/p/5501706.html
b,b+ 树 & linux磁盘存储 :https://www.cnblogs.com/vincently/p/4526560.html
b,b+树 & mysql索引 & 索引的结构优化:http://blog.codinglabs.org/articles/theory-of-mysql-index.html
树:
树(Tree)是n(n≥0)个结点的有限集T,并且当n>0时满足下列条件:
(1)有且仅有一个特定的称为根(Root)的结点;
(2)当n>1时,其余结点可以划分为m(m>0)个互不相交的有限集T1、T2 、…、Tm,每个集Ti(1≤i≤m)均为树,且称为树T的子树(SubTree)。
特别地,不含任何结点(即n=0)的树,称为空树。
如下就是一棵树的结构:
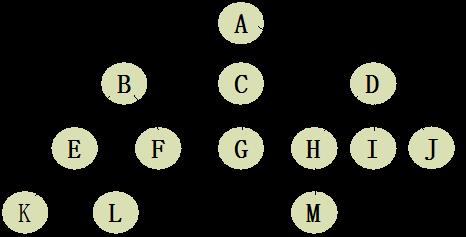
两种树:
- 有序树:若将树中每个结点的各子树看成是从左到右有次序的(即不能互换),则称该树为有序树
- 无序树:若将树中每个结点的各子树看成是从左到右无次序的(即可以互换),则称该树为无序树
多叉树的广度优先遍历与深度优先遍历
举个栗子:
多叉树 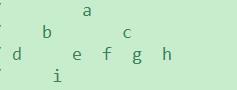
广度优先遍历:a b c d e f g h i
深度优先遍历:a b d e i c f g h (相当于二叉树的先序遍历)
实现:

public class MultiwayTree { private static MultiwayNode root; public MultiwayTree(){ // a // b c // d e f g h // i MultiwayNode h=new MultiwayNode("h"); MultiwayNode i=new MultiwayNode("i"); MultiwayNode g=new MultiwayNode("g"); MultiwayNode f=new MultiwayNode("f"); MultiwayNode d = new MultiwayNode("d"); MultiwayNode e = new MultiwayNode("e",i); MultiwayNode b = new MultiwayNode("b", d, e); MultiwayNode c = new MultiwayNode("c", f, g,h); root = new MultiwayNode("a", b, c); } //深度优先遍历 static void depthFirstSearch(MultiwayNode node){ if(node==null){ return; } List<MultiwayNode> children=node.children; if(children==null){ return; } System.out.print(node.value+" "); for(MultiwayNode no:children){ depthFirstSearch(no); } } //广度优先遍历 static void breadthFirstSearch(){ List<MultiwayNode> list=new ArrayList<MultiwayNode>(); list.add(root); breadthFirstSearch(list); } //广度优先遍历 static void breadthFirstSearch(List<MultiwayNode> nodes){ List<MultiwayNode> level=new ArrayList<MultiwayNode>(); for(MultiwayNode node:nodes){ System.out.print(node.value+" "); List<MultiwayNode> children=node.children; level.addAll(children); children.clear(); } if(level.size()>0){ breadthFirstSearch(level); } } public static void main(String[] args) { MultiwayTree head=new MultiwayTree(); depthFirstSearch(head.root); } } class MultiwayNode{ public String value; public List<MultiwayNode> children=null; public MultiwayNode(String value,MultiwayNode... nodes){ this.value=value; children=new ArrayList<MultiwayNode>(); for(MultiwayNode node:nodes){ children.add(node); } } }
二叉树:
二叉树是每个结点最多有两个孩子,且其子树有左右之分的有序树
二叉树的两个特殊形态
- 满二叉树:
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树
- 完全二叉树(Complete Binary Tree):
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树
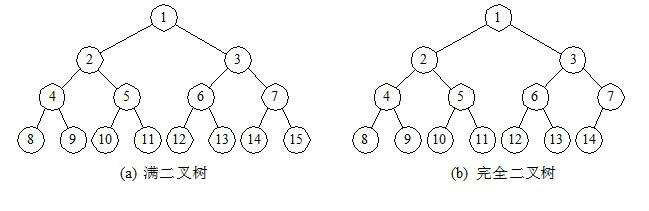
二叉树得到一般算法
求二叉树的最大深度:

int getMaxDeath(Node node) { if (node == null) { return 0; } int left = getMaxDeath(node.leftchild); int right = getMaxDeath(node.leftchild); return Math.max(left, right) + 1; }
求二叉树的最小深度:

int getMinDepth(Node root) { if (root == null) { return 0; } int left=getMinDepth(root.leftchild); int right=getMinDepth(root.rightchild); return Math.min(left, right) + 1; }
求二叉树的总节点数

//求二叉树的节点总数 int getTotalNumNode(Node root) { if (root == null) { return 0; } int left = getTotalNumNode(root.leftchild); int right = getTotalNumNode(root.rightchild); return left + right + 1; }
求二叉树种的叶子节点的个数

// 求二叉树中叶子节点的个数 int getNumForLeafNode(Node root) { if (root == null) { return 0; } if (root.leftchild == null && root.rightchild == null) { return 1; } return getNumForLeafNode(root.leftchild) + getNumForLeafNode(root.rightchild); }
求二叉树中第k层节点的个数

//求二叉树中第k层节点的个数 int getNumOfkLevelNode(Node root, int k) { if (root == null || k < 1) { return 0; } if (k == 1) { return 1; } int numsLeft = getNumOfkLevelNode(root.leftchild, k - 1); int numsRight = getNumOfkLevelNode(root.rightchild, k - 1); return numsLeft + numsRight; }
两个二叉树是否完全相同

boolean isSameTree(Node t1, Node t2) { if (t1 == null && t2 == null) { return true; } else if (t1 == null || t2 == null) { return false; } if(!t1.getValue().equals(t2.getValue())){ return false; } boolean left = isSameTree(t1.leftchild, t2.leftchild); boolean right = isSameTree(t1.rightchild, t2.rightchild); return left && right; }
两个二叉树是否互为镜像

//两个二叉树是否互为镜像 boolean isMirror(Node t1, Node t2) { if (t1 == null && t2 == null) { return true; } if (t1 == null || t2 == null) { return false; } if (!t1.getValue().equals(t2.getValue())) { return false; } return isMirror(t1.leftchild, t2.rightchild) && isMirror(t1.rightchild, t2.leftchild); }
翻转/镜像二叉树

// 翻转二叉树or镜像二叉树 Node mirrorTreeNode(Node root) { if (root == null) { return null; } Node left = mirrorTreeNode(root.leftchild); Node right = mirrorTreeNode(root.rightchild); root.leftchild = right; root.rightchild = left; return root; }
前根序遍历 父节点->左孩子->右孩子

// 前根序遍历 父节点->左孩子->右孩子 public void preOrder(Node no) { if (no != null) { printValue(no); preOrder(no.getLeftchild()); preOrder(no.getRightchild()); } }
中根序遍历 左孩子->父节点->右孩子

//中根序遍历 左孩子->父节点->右孩子 public void inOrder(Node no) { if (no != null) { inOrder(no.getLeftchild()); printValue(no); inOrder(no.getRightchild()); } }
后根序遍历 左孩子->右孩子->父节点

// 后根序遍历 左孩子->右孩子->父节点 public void reOrder(Node no) { if (no == null) { return; } reOrder(no.getLeftchild()); reOrder(no.getRightchild()); printValue(no); }
二叉查找树(Binary Sort Tree)(排序树/搜索树)
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
1) 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2) 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
3) 左、右子树也分别为二叉排序树;
4) 没有键值相等的节点。

二叉查找树的性质:
对二叉查找树进行中序遍历,即可得到有序的数列
二叉查找树的时间复杂度:
它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡。我们追求的是在最坏的情况下仍然有较好的时间复杂度,这就是平衡查找树设计的初衷
平衡二叉查找树(Balanced Binary Tree)(简称平衡二叉树)(avl树):
它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树
平衡因子(bf):
结点的左子树的深度减去右子树的深度,那么显然-1<=bf<=1
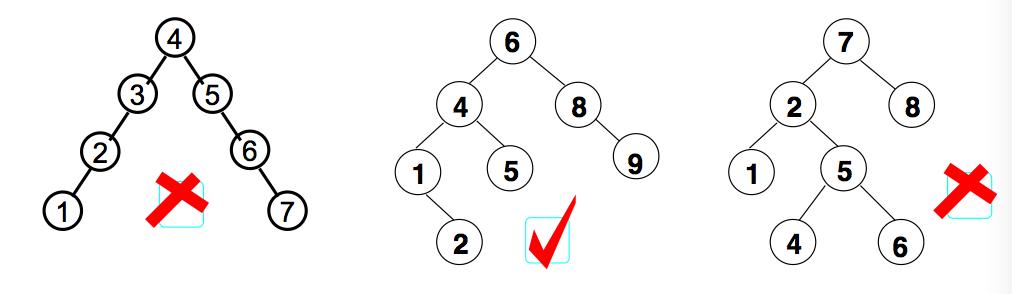
查询 & 插入 & 删除 时间复杂度:O(logn)
应用:
- windows对进程地址空间的管理用到了AVL树

// 判断是否为平衡二叉树 public boolean isBalanced(Node root, int depth) { if (root == null) { depth = 0; return true; } int leftDepth = 0; int rigthDepth = 0; boolean isLeftBalanced = isBalanced(root.getLeftchild(), leftDepth); boolean isRightBalanced = isBalanced(root.getLeftchild(), rigthDepth); if (isLeftBalanced && isRightBalanced) { int diff = leftDepth - rigthDepth; if (diff <= 1 || diff >= -1) { depth = leftDepth > rigthDepth ? leftDepth : rigthDepth + 1; return true; } } return false; }
- 节点是红色或黑色
- 根是黑色
- 所有叶子都是黑色(叶子是NIL节点)
- 从每个叶子到根的所有路径上不能有两个连续的红色节点
- 从任一节点到其每个叶子的所有简单路径 都包含相同数目的黑色节点
查询 & 插入 & 删除 时间复杂度:O(logn)
应用:
- 广泛用在C++的STL中。如map和set都是用红黑树实现的
- 著名的linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块
- epoll在内核中的实现,用红黑树管理事件块
- nginx中,用红黑树管理timer等
- Java的TreeMap实现
红黑树 vs avl树
- 插入:如果插入一个node引起了树的不平衡,AVL和RB-Tree都是最多只需要2次旋转操作,即两者都是O(1);
- 删除:最坏情况下,AVL需要维护从被删node到root这条路径上所有node的平衡性,因此需要旋转的量级O(logN),而RB-Tree最多只需3次旋转,只需要O(1)的复杂度。AVL的结构相较RB-Tree来说更为平衡,在插入和删除node更容易引起Tree的unbalance,因此在大量数据需要插入或者删除时,AVL需要rebalance的频率会更高。因此,RB-Tree在需要大量插入和删除node的场景下,效率更高。
- 查找:由于AVL高度平衡,因此AVL的search效率更高
map的实现只是折衷了两者在search、insert以及delete下的效率。总体来说,RB-tree的统计性能是高于AVL的。
Trie树(字典树)
B-树(平衡多路查找树)
一棵m阶的b树满足下列条件:
- 每个结点至多拥有m棵子树根结点至少拥有两颗子树(存在子树的情况下)
- 除了根结点以外,其余每个分支结点至少拥有 m/2 棵子树
- 所有的叶结点都在同一层上
- 有 k 棵子树的分支结点则存在 k-1 个关键码,关键码按照递增次序进行排列
- 关键字数量需要满足ceil(m/2)-1 <= n <= m-1
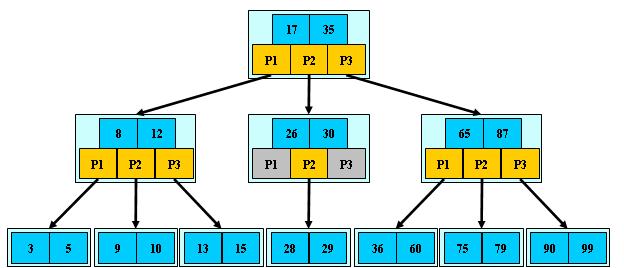
b树的特性:
- 关键字集合分布在整颗树中
- 任何一个关键字出现且只出现在一个结点中
- 搜索有可能在非叶子结点结束
- 其搜索性能等价于在关键字全集内做一次二分查找
查询,插入,删除 时间复杂度:O(logn)
B+树
B+树是B-树的变体,也是一种多路搜索树:
其定义基本与B-树同,除了:
- 非叶子结点的子树指针与关键字个数相同
- 非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间)
- 为所有叶子结点增加一个链指针
- 所有关键字都在叶子结点出现
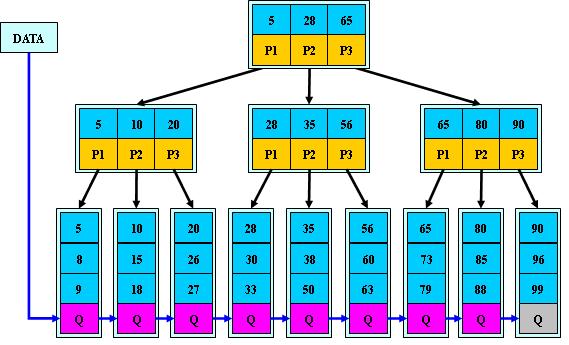 B+的特性:
B+的特性:
- 所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的
- 不可能在非叶子结点命中
- 非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层
- 更适合文件索引系统
查询,插入,删除 时间复杂度:O(logn)
应用:InnoDB索引 MyISAM索引
B*树
是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针
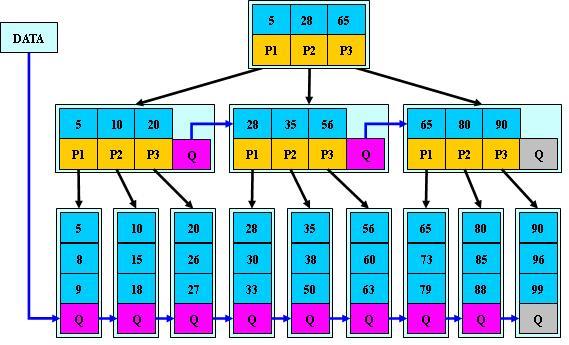
B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3
(代替B+树的1/2);
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据
复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父
结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分
数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字
(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之
间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;
所以,B*树分配新结点的概率比B+树要低,空间使用率更高;
R树
R树是B树在高维空间的扩展,是一棵平衡树。每个R树的叶子结点包含了多个指向不同数据的指针,这些数据可以是存放在硬盘中的,也可以是存在内存中。根据R树的这种数据结构,当我们需要进行一个高维空间查询时,我们只需要遍历少数几个叶子结点所包含的指针,查看这些指针指向的数据是否满足要求即可。这种方式使我们不必遍历所有数据即可获得答案,效率显著提高。下图1是R树的一个简单实例:
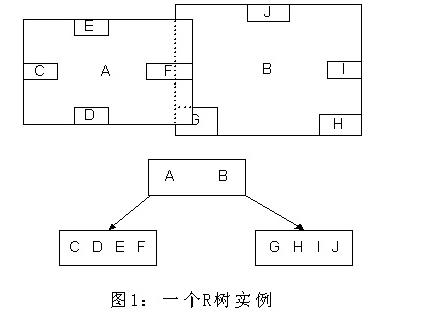
以上是关于经典算法二叉树 & 平衡二叉树 & 红黑树的主要内容,如果未能解决你的问题,请参考以下文章
