一、定义
①堆通常是可被视为完全二叉树的数组。
②堆中任意节点的数值总是大于或等于其左右子节点,为大根堆。
③堆中任意节点的数值总是小于或等于其左右子节点,为小根堆。
二、存储
对于任意节点T[i]
①若其父节点存在,为T[(i - 1) / 2]
②若其左兄弟节点存在,为T[i - 1]
③若其右兄弟节点存在,为T[i + 1]
④若其左子节点存在,为T[i * 2 + 1]
⑤若其右子节点存在,为T[i * 2 + 2]
数组表示

二叉树表示
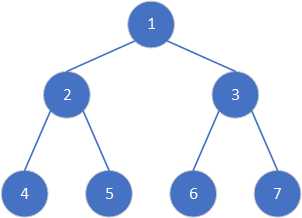
三、调整(大根堆)
①若数值大于选择节点的左右子节点存在,则交换选择节点与左右子节点中数值较大者。
②若数值大于选择节点的左右子节点不存在,则该选择节点的调整结束。
具体过程如下:
假设选择根节点进行调整。
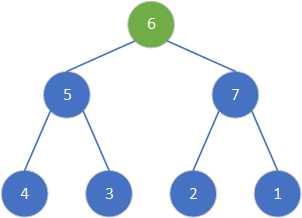
将选择节点与数值较大的右子节点进行交换。至此调整结束,不存在大于选择节点的左右子节点。
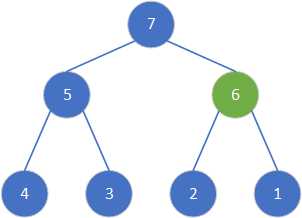
四、排序
①构建大根堆。从最后一个非叶节点开始,从下到上、从右到左选择每个非叶节点进行一次调整。
②调整堆结构。从最后一个节点开始,从下到上、从左到右将每个节点与根节点进行交换后,选择根节点进行一次调整。已经与根节点交换过的位置不参与调整。
具体过程如下:
选择7进行调整。
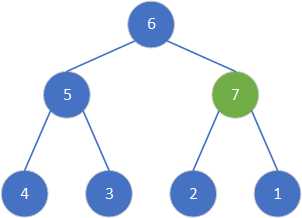
选择5进行调整。
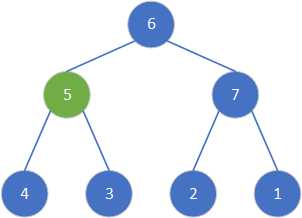
选择6进行调整。

交换1和7,选择根节点1进行调整。
虽然7大于2,但7所处的位置已与根节点进行过交换,所以不参与调整。
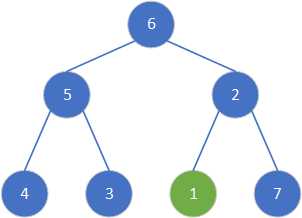
交换1和6,选择根节点1进行调整。
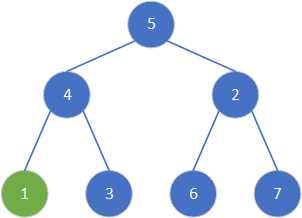
交换3和5,选择根节点3进行调整。
虽然5大于3,但5所处的位置已与根节点进行过交换,所以不参与调整。
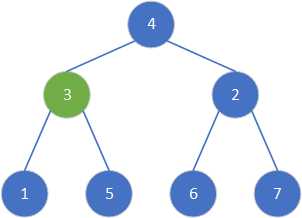
交换1和4,选择根节点1进行调整。
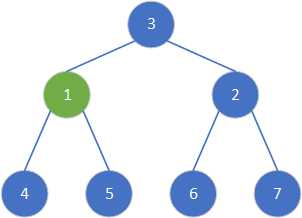
交换2和3,选择根节点2进行调整。
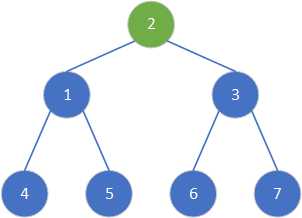
交换1和2,选择根节点1进行调整。
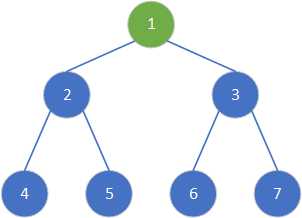
排序结束,二叉树对应的数组有序。
五、实现
public class HeapSort { private static void swap(int[] array, int i, int j) { int temp = array[i]; array[i] = array[j]; array[j] = temp; } private static void adjust(int[] array, int i, int length) { int temp = array[i]; for (int j = i * 2 + 1; j < length; j = j * 2 + 1) { if (j + 1 < length && array[j] < array[j + 1]) j = j + 1; if (array[j] > temp) { array[i] = array[j]; i = j; } else break; } array[i] = temp; } public static void sort(int[] array) { for (int i = (array.length - 1) / 2; i >= 0; i--) adjust(array, i, array.length); for (int j = array.length - 1; j > 0; j--) { swap(array, 0, j); adjust(array, 0, j); } } }