使用matplotlib模拟e^x的麦克劳林展开式
Posted Don*Quixote
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了使用matplotlib模拟e^x的麦克劳林展开式相关的知识,希望对你有一定的参考价值。
使用matplotlib模拟下e^x的麦克劳林展开式,用plt画图一开始觉得还是挺有意思的。
import matplotlib.pyplot as plt import numpy as np import random \'\'\' e^x的麦克劳林展开式: e^x= f(0)+ f′(0)x+ f″(0)x ²/ 2!+...+ fⁿ(0)x^n/n!+Rn(x) =1+x+x^2/2!+x^3/3!+...+x^n/n!+Rn(x) \'\'\' # 阶乘函数 def factorial(n): x = 1 for i in range(1,n+1): x = x * i return x # y值函数 def consY(n,x): y = 1 for i in range(1,n): y += x**i/factorial(i) return y # 生成图像 def moniPlot(n,x): # 定义一个颜色集合 colors = [\'g\',\'b\',\'black\',\'cyan\',\'lightgreen\',\'yellow\',\'deeppink\',\'darkorchid\'] plt.figure() # 原函数 y = np.e**x # 画原函数图像并进行标记 plt.plot(x,y,\'r-\',linewidth=2,label=\'e^x\') # 麦克劳林展开添加到图像上 for i in range(2,n): y = consY(i,x) # 随机选择颜色 color = colors[random.randint(0,len(colors)-1)] linestyle = \'--\' # 画图像,并对最后一个进行标记 if i == n: plt.plot(x,y,color=color,linewidth=1,linestyle=linestyle,label="nearly e^x") else: plt.plot(x,y,color=color,linewidth=1,linestyle=linestyle) plt.plot(x,y,color=color,linewidth=1,linestyle=linestyle) #添加注释 plt.text(1.2, consY(10,3.9),"Maclaurin\'s series of e^x ",size=12) # 将标记绘制图例,位置为于中间左侧 plt.legend([\'e^x\',"nearly e^x"], loc = \'center left\') plt.show() # 定义 x , y x = np.linspace(1,4,80) # 原函数 # y = np.e**x # Maclaurin展开 3项 # y1 = consY(2,x) # 展开 4项 # y2 = consY(3,x) # tylor 5项 # y3 = consY(4,x) # 调用生成图像 moniPlot(10,x) # 关闭图 plt.close()
运行代码,plt展示的结果如下(展开式的项数越多,越接近原函数):
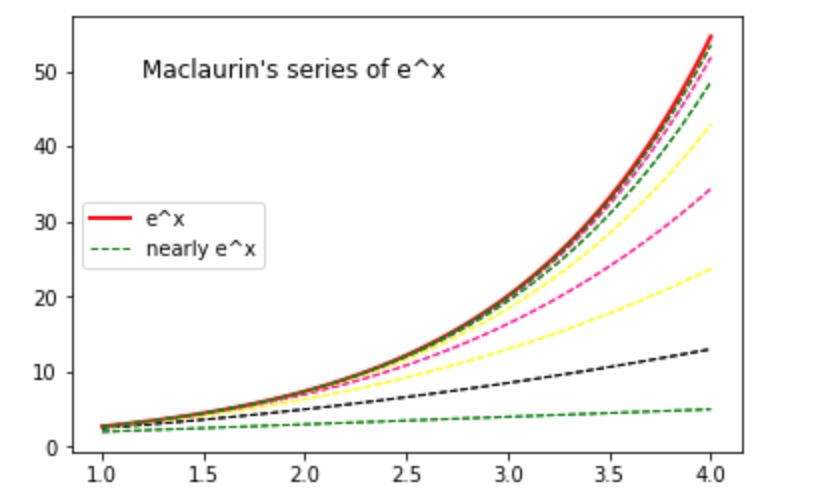
以上是关于使用matplotlib模拟e^x的麦克劳林展开式的主要内容,如果未能解决你的问题,请参考以下文章