7-1 求组合数(15 分)
1.题目
本题要求编写程序,根据公式C?n?m??=?m!(n?m)!??n!??算出从n个不同元素中取出m个元素(m≤n)的组合数。
建议定义和调用函数fact(n)计算n!,其中n的类型是int,函数类型是double。
输入格式:
输入在一行中给出两个正整数m和n(m≤n),以空格分隔。
输出格式:
按照格式“result = 组合数计算结果”输出。题目保证结果在double类型范围内。
2.提交列表
3.设计思路(流程图)
定义变量和子函数,输入m,n,通过子函数求得新的y,m,n,最后由表达式输出结果。
子函数
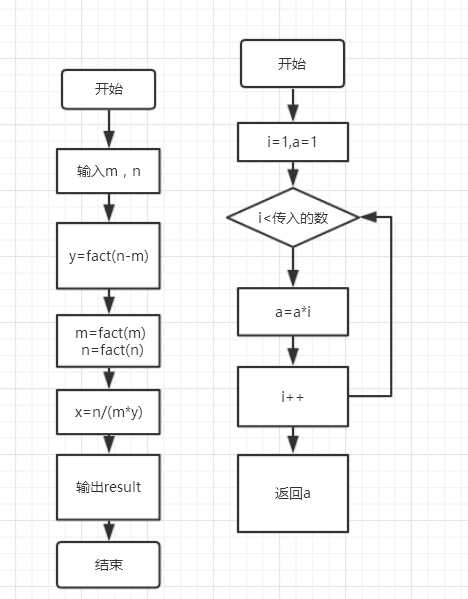
代码如下
#include<stdio.h>
double fact(double z)
{
double i,a=1;
for(i=1;i<=z;i++)
a=a*i;
return a;
}
int main()
{
double x,y,m,n;
scanf("%lf %lf",&m,&n);
y=fact(n-m);
m=fact(m);
n=fact(n);
x=n/(m*y);
printf("result = %.0lf",x);
}
4.答案结果
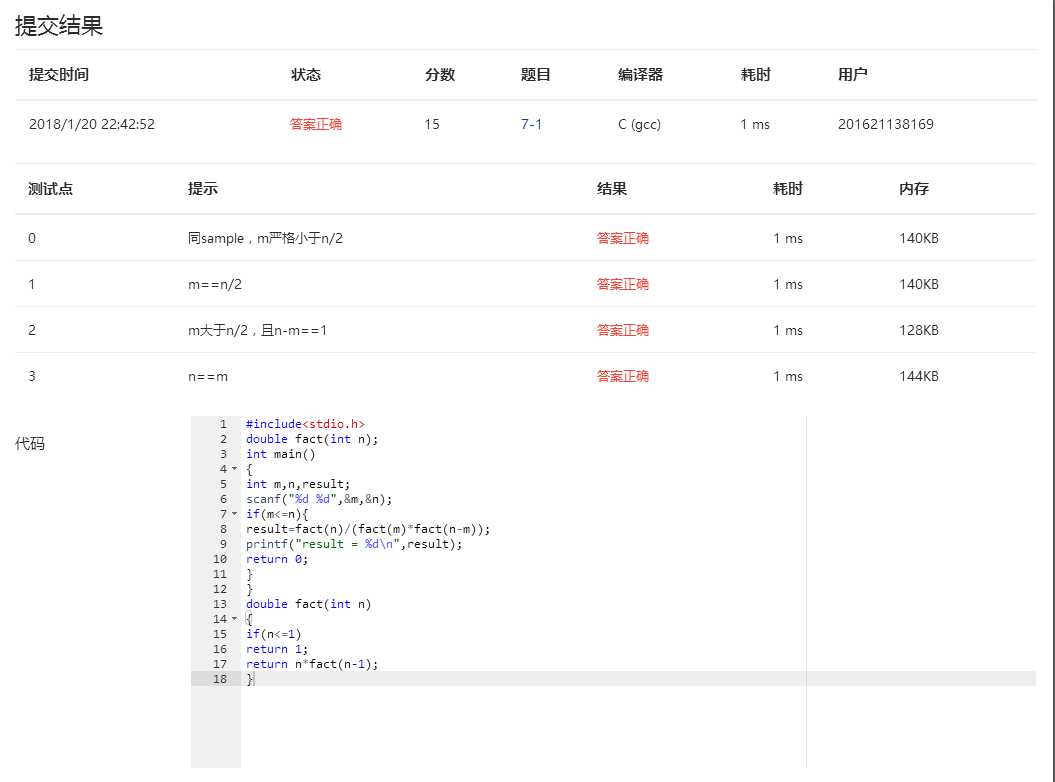
7-3 求幂之和(15 分)
1.题目
本题要求编写程序,计算sum=2?1??+2?2??+2?3??+?+2?n??。可以调用pow函数求幂。
输入格式:
输入在一行中给出正整数n(≤10)。
输出格式:
按照格式“result = 计算结果”输出。
2.提交列表
3.设计思路(流程图)
定义变量和子函数,循环求和,并输出
子函数如下
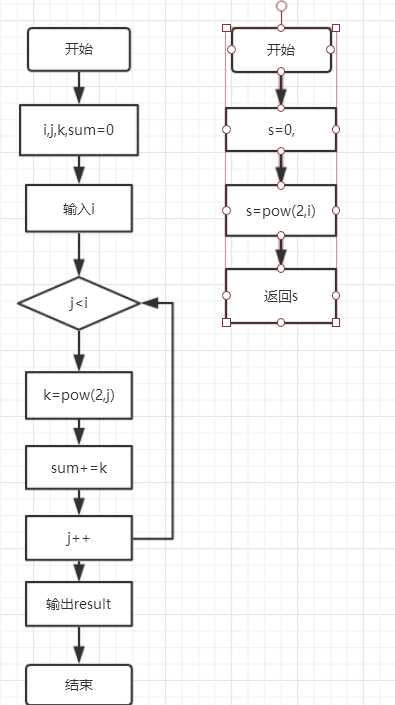
代码如下
#include<stdio.h>
#include<math.h>
int fact(int i);
main()
{
int i,j,k,sum=0;
scanf("%d",&i);
for(j=1;j<=i;j++){
k=pow(2,j);
sum+=k;
}
printf("result = %d",sum);
}
int fact(int i)
{
int s;
s=pow(2,i);
return s;
}
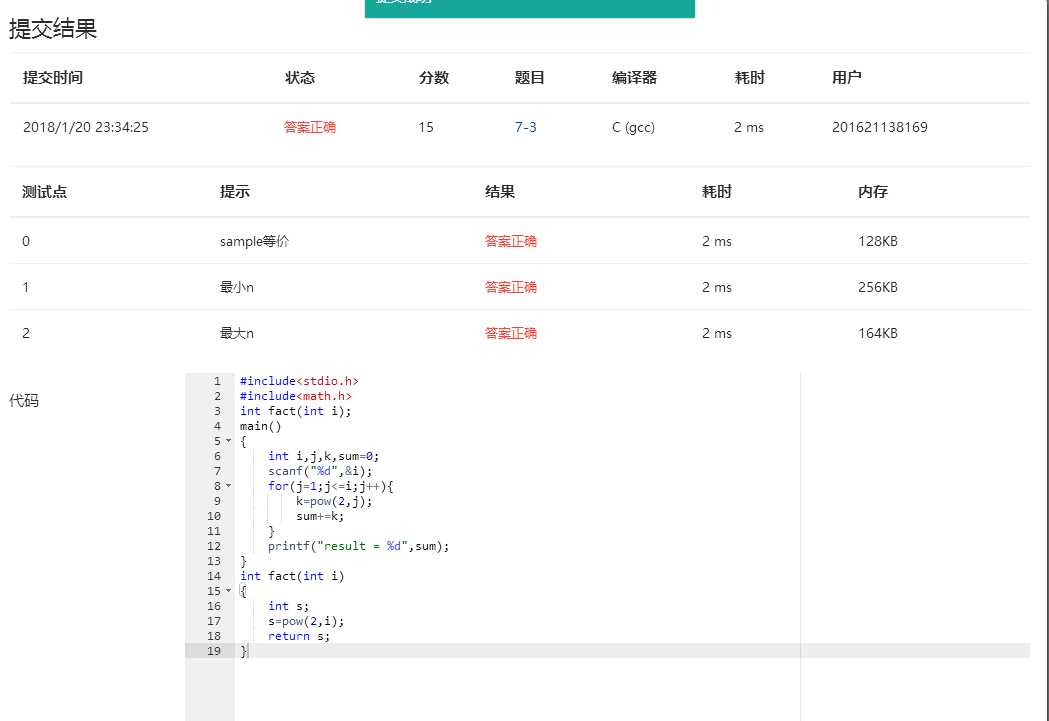
4.答案结果
7-10 判断素数(10 分)
1.题目
本题的目标很简单,就是判断一个给定的正整数是否素数。
输入格式:
输入在第一行给出一个正整数N(≤ 10),随后N行,每行给出一个小于2?31??的需要判断的正整数。
输出格式:
对每个需要判断的正整数,如果它是素数,则在一行中输出Yes,否则输出No。
2.提交结果
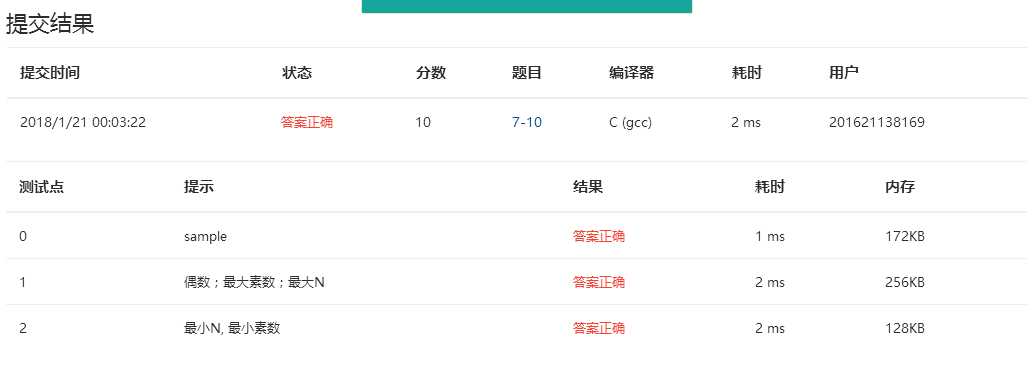
3.设计思路(流程图)
先定义一个主函数,输入a值,循环选择判断是否是素数
子函数
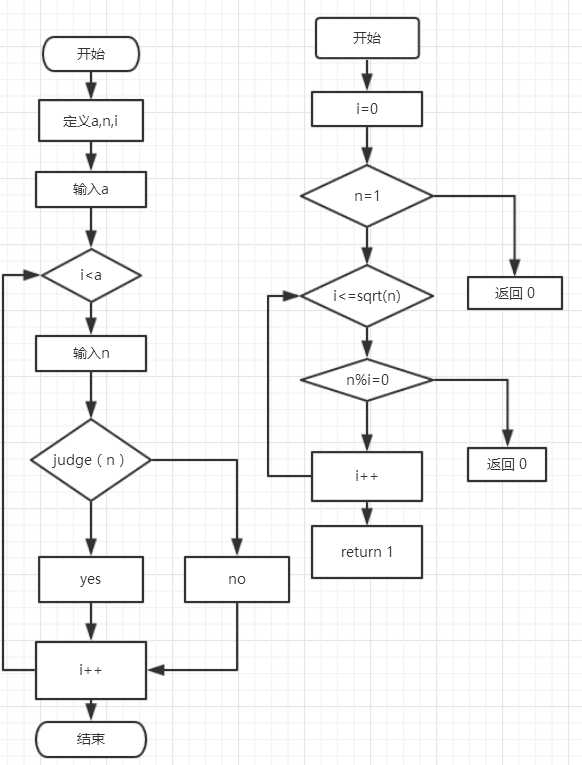
代码如下
#include<stdio.h>
#include<math.h>
int main()
{
int judge(int n);
int a,n,i;
scanf("%d",&a);
for(i=0;i<a;i++){
scanf("%d",&n);
if(judge(n)){
printf("Yes\\n");
}
else
printf("No\\n");
}
}
int judge(int n){
int i;
if(n==1)
return 0;
for(i=2;i<=sqrt(n);i++){
if(n%i==0){
return 0;
}
}
return 1;
}
4.答案结果
二、同学互评
同学代码(7.3)
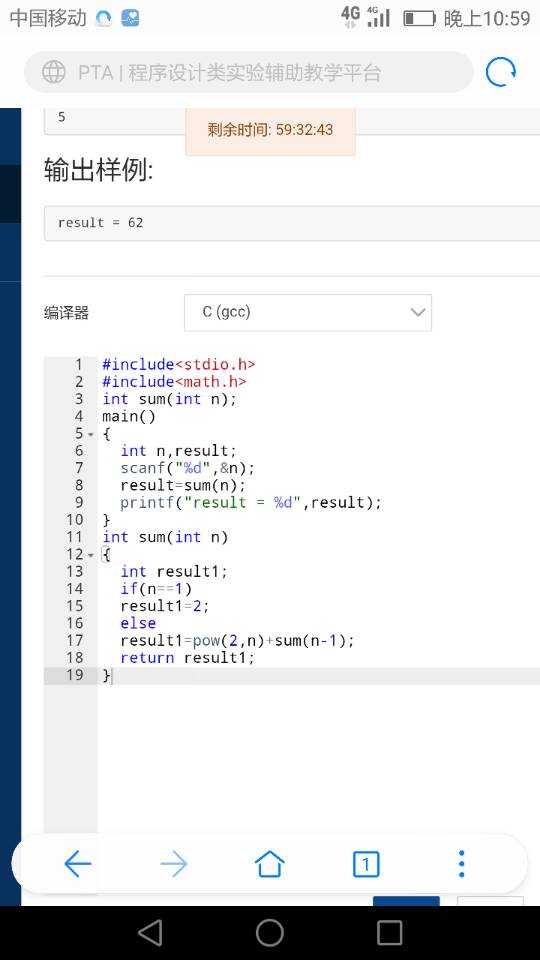
我的代码
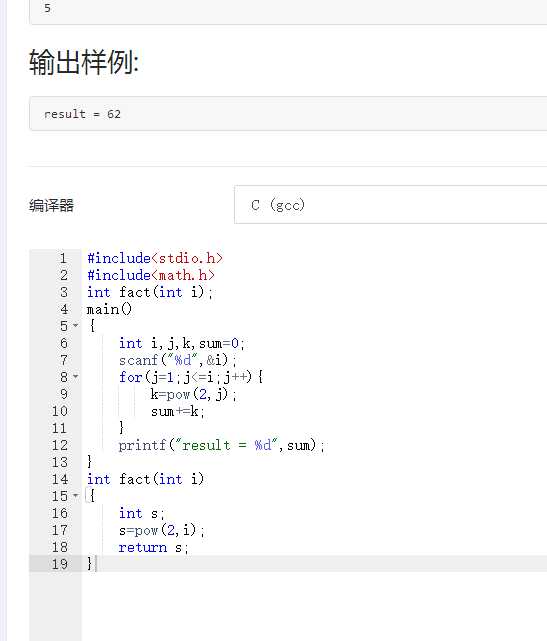
我的代码相比较他的代码更加的简洁,思维简单清晰,两者的子函数表带形式不一样
都有各自的优缺点,我更喜欢自己的代码。
四、本周学习总结
1.本周你学会了什么?
1.本周学会如何简单的声明一个函数并且调用函数;
2.还有return0和return1的用法
3.知道了如何讲复杂的代码化为一个一个子函数代码
2.本周的内容,还有那些内容不会?
1.在一些概念方面还是容易出错,并且不能够自己独立的很好的写出代码,属于模仿别人代码的阶段。