一、红黑树特性
1.节点只能为红色或者黑色。
2.根节点为黑色。
3.叶节点(NIL)为黑色。
4.红色节点的子节点必须时黑色节点。
5.任意节点到达该节点的子孙节点的路径包含相同数目的黑色节点。
二、红黑树基本操作
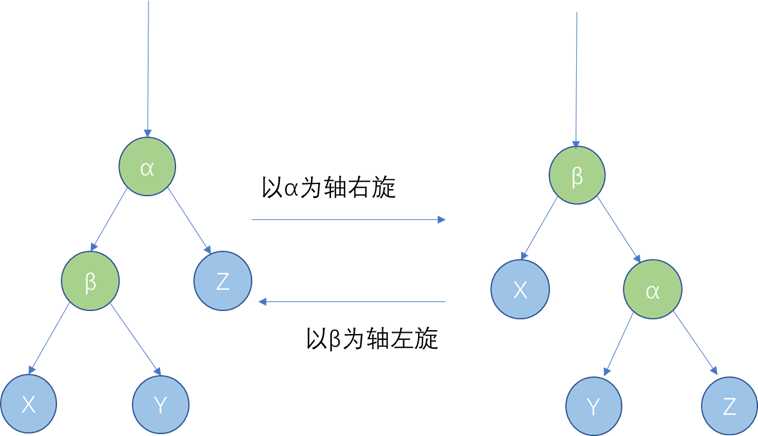
三、插入节点
将红黑树作为一棵普通的搜索树进行插入,将插入节点涂为红色。之后有三种情况:
1.若当前节点为根节点,将插入节点涂为黑色。
2.若当前节点的父节点为黑色,不需要调整,仍然是红黑树。
3.若当前节点的父节点为红色,将红色节点移动到根节点后涂黑即可,依然有三种情况:
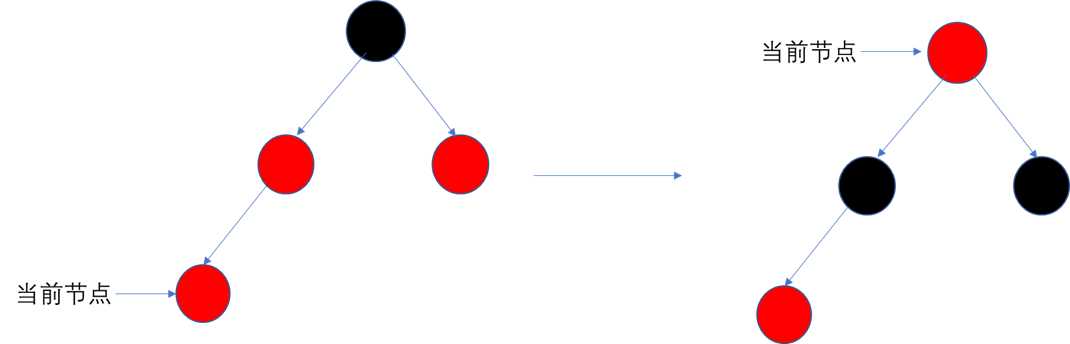
Case 1:若当前节点的叔叔节点(父节点的兄弟节点)为红色
①将父节点涂为黑色
②将叔叔节点涂为黑色
③将祖父节点涂为红色
④将祖父节点设为当前节点继续进行操作
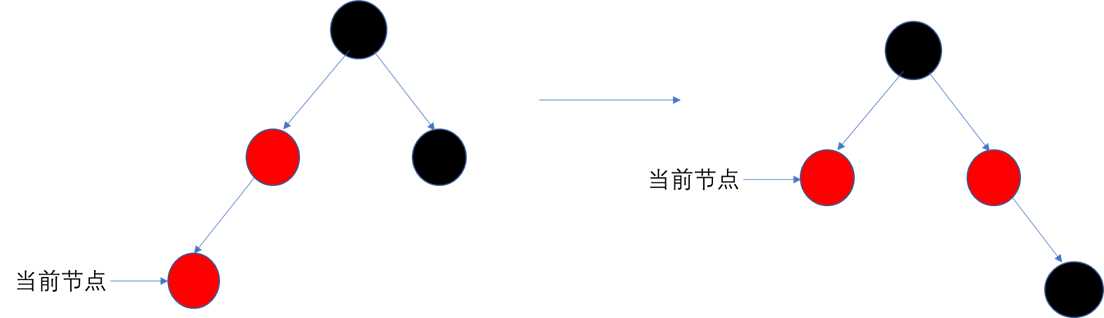
Case 2:若当前节点的叔叔节点为黑色,且当前节点为其父节点的右子节点
①将父节点设为当前节点
②以当前节点为轴进行左旋

Case 3:若当前节点的叔叔节点为黑色,且当前节点为其父节点的左子节点
①将父节点涂为黑色
②将祖父节点涂为红色
③以祖父节点为轴进行右旋
四、删除操作
将红黑树作为一棵普通的搜索树进行删除。
1.若删除节点没有子节点,则直接将其删除。
2.若删除节点只有一个子节点,则删除该节点后其子节点代替其位置。
3.若删除节点有两个子节点,交换删除节点与其后继节点。重复直到删除节点满足①或②,删除之。
删除结束后对红黑树进行调整
1.若删除节点为红色,不需要调整,仍然是红黑树。
2.若删除节点为黑色,那么我们假设代替删除节点初始位置的节点继承了删除节点的黑色,将这个多余的黑色向树根移动即可。存在三种情况:
(1)若多余的黑色所在的节点为红色,则将该节点涂为黑色即可恢复红黑树性质。
(2)若多余的黑色所在的节点为黑色,且该节点为根,则不需要调整,仍然是红黑树。
(3)若多余的黑色所在的节点为黑色,但该节点不为根,则存在四种情况
Case 1:当前节点的兄弟节点为红色
①将当前节点的兄弟节点涂为黑色
②将当前节点的父节点涂为红色
③以当前节点的父节点为轴进行左旋
Case 2:当前节点的兄弟节点为黑色,且兄弟节点的子节点均为黑色
①将当前节点的兄弟节点设为红色
②将当前节点多余的黑色移动到其父节点
Case 3:当前节点的兄弟节点为黑色,且兄弟节点的左子节点为红色,右子节点为黑色
①将当前节点的兄弟节点的左子节点涂为黑色
②将当前节点的兄弟节点涂为红色
③以当前节点的兄弟节点为轴进行右旋
Case 4:当前节点的兄弟节点为黑色,且兄弟节点的右子节点为红色,左子节点为红色或黑色
①将当前节点的兄弟节点涂为其父节点的颜色
②将当前节点的父节点涂为黑色
③将当前节点的兄弟节点的右子节点涂为黑色
④以当前节点的父节点为轴进行左旋
⑤将当前节点设置为根节点