CS3334 Lecture 1

Posted 2020-10-21 Charonnnnn

Lecture 1: Complexity Analysis

How to measure Running time: Use a function to model the running time of a program or procedure.

• Assume an abstract machine and count the number of “steps” executed by an algorithm

 

Function: In mathematics, a function is a relation between a set of inputs and a set of allowed outputs with the property that each input is related to exactly one output

 

How to Model Running Time as a function:

Resultant function: f(n) = 3n + 4 = O(n)   will be explained in the follow

 

---

Compare the functions of Running Time models:

Consider the order of growth of running time, not the actual value

The order of growth rate

• Give a simple characterization of the algorithm’s efficiency 
• Allow us to compare the relative performance of alternative algorithms

In the analysis of algorithms, we need to consider the performance of algorithms when applied to very very big input datasets, e.g., very large n (i.e., asymptotic analysis)

T_A(n) = 100n + 50

T_B(n) = (0.5)n² + 4.5n + 5

 T_A(n) > T_B(n) if n < c,   but T_A(n) < T_B(n) if n > c

 

Asymptotic Notation - notations to express the growth rate of a function (Just for function)

A way to compare \'size\' of functions:

– O-notation (“Big-oh”) ≈≤ (upper bound)

– Ω-notation (“Big-omega”) ≈≥ (lower bound)

– θ-notation (“theta”) ≈= (in between)

 

---

O-notation:

f(n) = O(g(n)) to                f(n) ≤ c*g(n)

• Indicate that f(n) is a member of the set O(g(n))
• Give that g(n) is an upper bound for f(n) to within a constant factor

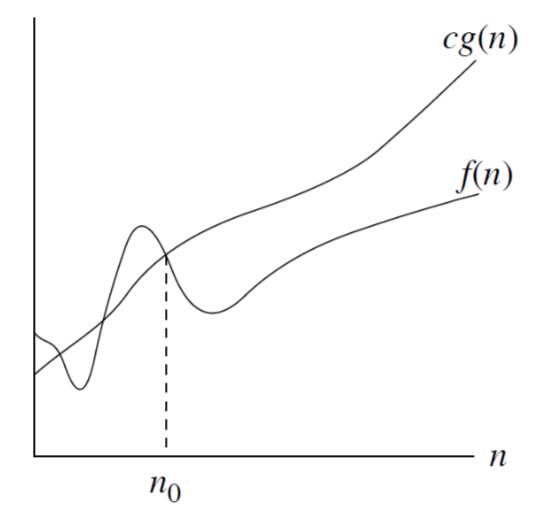f(n) = O(g(n)): there exist positive constants c and n₀ such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n₀

 

Ω-notation:

f(n) = Ω(g(n)) to         f(n) ≥ c*g(n)

• Indicate that f(n) is a member of the set Ω(g(n))
• Give that g(n) is a lower bound for f(n) to within a constant factor

f(n) = Ω(g(n)): there exist positive constants c and n₀ such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n₀

 

θ-notation

f(n) = θ(g(n)) to          c₁g(n) ≤ f(n) ≤ c₂g(n)

• Indicate that f(n) is a member of the set O(g(n)), give that g(n) is an upper bound for f(n) to within a constant factor
• Indicate that f(n) is a member of the set Ω(g(n)), give that g(n) is a lower bound for f(n) to within a constant factor 

f(n) = θ(g(n)) if and only if (1) f(n) = O(g(n)) and (2) f(n) = Ω(g(n))

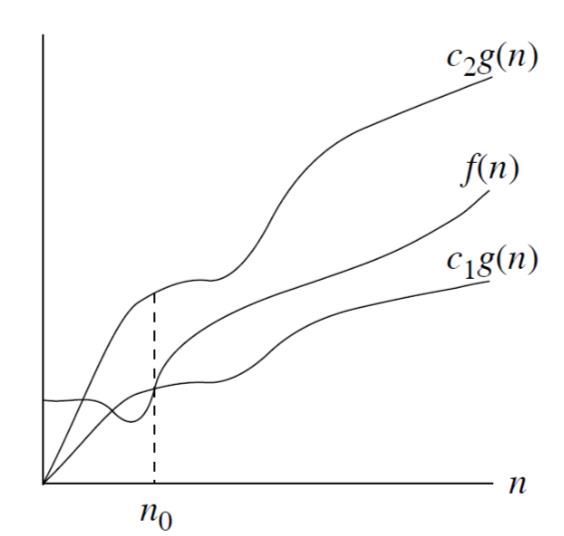f(n) = θ(g(n)): there exist positive constants c₁, c₂ and n₀ such that 0 ≤ c₁g(n) ≤ f(n) ≤ c₂g(n) for all n ≥ n₀

 

 

---

Find the O-notation of a function

The function must with a constant number of terms

and fulfill three rules:

Rule 1: sort the terms of the function in decreasing order of their growth rates

constant < logn < n < nlogn ≤ nlogn^c < n² < n³ < 2ⁿ

Rule 2: Ignore the lower order terms (only keep the leading term)

Rule 3: Ignore the coefficient of the leading term 

 

Example 1:

1. By Rule #1: f(n) = 4n³ + 5n + 1000logn

2. By Rule #2: f(n) = O(4n³)

3. By Rule #3: f(n) = O(n³)

n³ will dominate the growth rate so ignore the other terms and constant

Example 2:

An arithmetic progression:

1+2+...+(n-1)+n is not O(n) but O(n²)

1+2+...+(n-1)+n = [(1+n)n]/2 = n²/2 + n/2 = O(n²/2) = O(n²)

 

The same rules can be used to find the Ω-notation of a function

Transpose symmetry property

– f(n) = O(g(n)) if and only if g(n) = Ω(f(n))

– In other words, if g(n) is the asymptotic upper bound of f(n), then f(n) is the asymptotic lower bound of g(n), and vice versa.

 

---

Time Complexity               

(Space complexity = space in memory)

Time complexity related to input size n and running time. For a fixed input size n, running time may still depend on the input data (e.g., data distribution and input order)

NOTE: A function to describe the (best/worst/average) case.  For each case, you can find three notations

-Best case time complexity T_b(n):                  

• The smallest time over all inputs of size n

-Worst case time complexity T_w(n): 

• The largest time over all inputs of size n 
• Give us a performance guarantee that is independent of input data

-Average case time complexity T (n):

• The average time over all inputs of size n
• Need an assumption on an input distribution (e.g., in uniform distribution, each possible input is equally likely to happen)
• Allow us to predict the performance in practice if our assumption on input distribution is realistic