Hihocoder 二分图一·二分图判定

Posted 2020-07-06 奇迹不是因果的积累，而是宿命的选择

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

大家好，我是小Hi和小Ho的小伙伴Nettle，从这个星期开始由我来完成我们的Weekly。

新年回家，又到了一年一度大龄剩男剩女的相亲时间。Nettle去姑姑家玩的时候看到了一张姑姑写的相亲情况表，上面都是姑姑介绍相亲的剩男剩女们。每行有2个名字，表示这两个人有一场相亲。由于姑姑年龄比较大了记性不是太好，加上相亲的人很多，所以姑姑一时也想不起来其中有些人的性别。因此她拜托我检查一下相亲表里面有没有错误的记录，即是否把两个同性安排了相亲。

OK，让我们愉快的暴力搜索吧！

才怪咧。

对于拿到的相亲情况表，我们不妨将其转化成一个图。将每一个人作为一个点(编号1..N)，若两个人之间有一场相亲，则在对应的点之间连接一条无向边。(如下图)

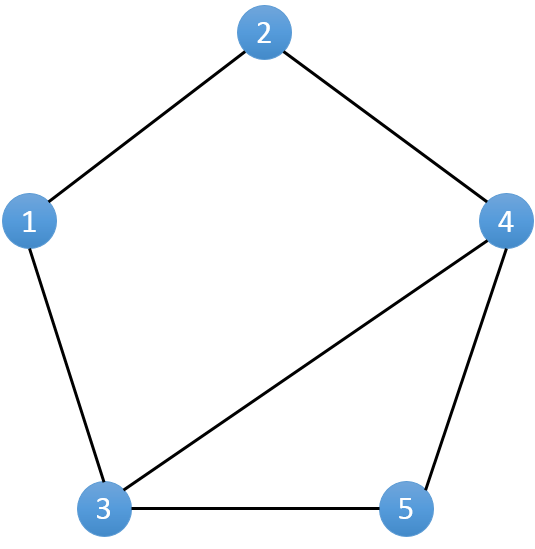
因为相亲总是在男女之间进行的，所以每一条边的两边对应的人总是不同性别。假设表示男性的节点染成白色，女性的节点染色黑色。对于得到的无向图来说，即每一条边的两端一定是一白一黑。如果存在一条边两端同为白色或者黑色，则表示这一条边所表示的记录有误。

由于我们并不知道每个人的性别，我们的问题就转化为判定是否存在一个合理的染色方案，使得我们所建立的无向图满足每一条边两端的顶点颜色都不相同。

那么，我们不妨将所有的点初始为未染色的状态。随机选择一个点，将其染成白色。再以它为起点，将所有相邻的点染成黑色。再以这些黑色的点为起点，将所有与其相邻未染色的点染成白色。不断重复直到整个图都染色完成。(如下图)

在染色的过程中，我们应该怎样发现错误的记录呢？相信你一定发现了吧。对于一个已经染色的点，如果存在一个与它相邻的已染色点和它的颜色相同，那么就一定存在一条错误的记录。(如上图的4，5节点)

到此我们就得到了整个图的算法：

 

1. 选取一个未染色的点u进行染色
2. 遍历u的相邻节点v：若v未染色，则染色成与u不同的颜色，并对v重复第2步；若v已经染色，如果 u和v颜色相同，判定不可行退出遍历。
3. 若所有节点均已染色，则判定可行。

接下来就动手写写吧！

输入

第1行：1个正整数T(1≤T≤10)

接下来T组数据，每组数据按照以下格式给出：

 

第1行：2个正整数N,M(1≤N≤10,000，1≤M≤40,000)

第2..M+1行：每行两个整数u,v表示u和v之间有一条边

输出

第1..T行：第i行表示第i组数据是否有误。如果是正确的数据输出”Correct”，否则输出”Wrong”

样例输入

2
5 5
1 2
1 3
3 4
5 2
1 5
5 5
1 2
1 3
3 4
5 2
3 5

样例输出

 

Wrong
Correct

 1 #include <iostream>
 2 #include <cstring>
 3 #include <cstdio>
 4 #include <cmath>
 5 #include <set>
 6 #include <map>
 7 #include <queue>
 8 #include <vector>
 9 #include <cstdlib>
10 #include <algorithm>
11 
12 #define ls u << 1
13 #define rs u << 1 | 1
14 #define lson l, mid, u << 1
15 #define rson mid + 1, r, u << 1 | 1
16 #define INF 0x3f3f3f3f
17 
18 using namespace std;
19 typedef long long ll;
20 const int M = 1e4 + 100;
21 const int mod = 2147483647;
22 int c[M];
23 vector<int>G[M];
24 
25 bool dfs(int u) {
26     for(int i = 0; i < G[u].size(); i++) {
27         int co = G[u][i];
28         if(c[co] == -1) {
29             c[co] = c[u] ^ 1;
30             if(!dfs(co)) return false;
31         } else {
32             if(c[co] == c[u]) return false;
33         }
34     }
35     return true;
36 }
37 
38 int main() {
39     int T,n,m;
40     cin>>T;
41     while(T--) {
42         scanf("%d %d",&n,&m);
43         memset(c,-1,sizeof(c));
44         while(m--) {
45             int a,b;
46             scanf("%d %d",&a,&b);
47             G[a].push_back(b);
48             G[b].push_back(a);
49         }
50         bool isGO = true;
51         for(int i = 1; i <= n && isGO; i++) {
52             if(c[i] == -1) {
53                 c[i] = 0;
54                 if(!dfs(i)) isGO = false;
55             }
56         }
57         if(isGO) puts("Correct");
58         else puts("Wrong");
59         for(int i = 1; i <= n; i++) G[i].clear();
60     }
61     return 0;
62 }