LCT[TPLY]
资料推荐
题目
https://www.luogu.org/problemnew/show/2147
https://www.luogu.org/problemnew/show/3690
https://www.luogu.org/problemnew/show/2387
https://www.luogu.org/problemnew/show/3203
资料
http://www.cnblogs.com/zhoushuyu/p/8137553.html
https://www.cnblogs.com/BLADEVIL/p/3510997.html
http://blog.csdn.net/qq_33330876/article/details/53580270
http://blog.csdn.net/tgop_knight/article/details/44539555
正文
讲到LCT,我们不得不提到一个人
没错,就是tarjan
在之前的学习中,我们学习了
Tarjan求LCA
Tarjan求强连通分量
Tarjan求桥,求割点
Tarjan的Splay
现在又要来一种
\\[LCT\\]
说到树链剖分,必须要提到它的好基友
\\[树链剖分\\]
和他的兄弟(一个Tarjan生的)
\\[Splay\\]
树链剖分:
LCT多变灵活,树链剖分成熟稳重
各有各的优势(不要以为学了LCT就不用学树剖了,有些代码树剖更方便)
树剖很好学,我个人是对着树剖的代码板子看一遍就理解了
https://www.luogu.org/problemnew/show/3384
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#define rg register int
#define ll long long
#define RG register
#define il inline
#define INF 2147483647
using namespace std;
il int gi()
{
rg x=0,o=0;RG char ch=getchar();
while(ch!=‘-‘ && (ch<‘0‘||ch>‘9‘)) ch=getchar();
if(ch==‘-‘) o=1,ch=getchar();
while(‘0‘<=ch&&ch<=‘9‘) x=(x<<1)+(x<<3)+ch-‘0‘,ch=getchar();
return o?-x:x;
}
#define SZ 200010
int n,m,root,cnt,opt;ll mo;
struct Edge{int to,nxt;}e[SZ];
int Ehead[SZ],Ecnt=2;
il void Eadd(rg u,rg v)
{
e[Ecnt]=(Edge){v,Ehead[u]};
Ehead[u]=Ecnt++;
e[Ecnt]=(Edge){u,Ehead[v]};
Ehead[v]=Ecnt++;
}
int w[SZ],fa[SZ],id[SZ],rid[SZ],dep[SZ],son[SZ],siz[SZ],top[SZ];
il void pou_debug()
{
for(rg i=1;i<=n;++i)
printf("%d %d %d %d %d %d\\n",fa[i],id[i],dep[i],son[i],siz[i],top[i]);
}
void dfs1(rg u,rg ff)
{
fa[u]=ff,dep[u]=dep[ff]+1,siz[u]=1;
for(rg v,i=Ehead[u];i;i=e[i].nxt)
{
v=e[i].to;
if(v==ff) continue;
dfs1(v,u);
siz[u]+=siz[v];
if(!son[u]||siz[v]>siz[son[u]])
son[u]=v;
}
}
void dfs2(rg u,rg tp)
{
top[u]=tp;id[u]=++cnt;rid[cnt]=u;
if(!son[u]) return;
dfs2(son[u],tp);
for(rg v,i=Ehead[u];i;i=e[i].nxt)
{
v=e[i].to;
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
#define lson (rt<<1)
#define rson (rt<<1|1)
struct Segtree{int l,r;ll len,sum,mark;}tr[400040];
il void Seg_debug()
{
for(rg i=1;i<=n*3;++i)
cout<<tr[i].l<<‘ ‘<<tr[i].r<<‘ ‘<<tr[i].len<<‘ ‘<<tr[i].sum<<‘ ‘<<tr[i].mark<<endl;
}
il void pushup(rg rt)
{
tr[rt].sum=(tr[lson].sum+tr[rson].sum)%mo;
}
void build(rg rt,rg l,rg r)
{
tr[rt].l=l,tr[rt].r=r,tr[rt].len=r-l+1;
if(l==r) {tr[rt].sum=w[rid[l]]%mo;return;}
rg mid=l+r>>1;
build(lson,l,mid);
build(rson,mid+1,r);
pushup(rt);
}
il void pushdown(rg rt)
{
if(tr[rt].mark)
{
ll mark=tr[rt].mark;
tr[lson].mark+=mark;
tr[rson].mark+=mark;
tr[lson].sum=(tr[lson].sum+mark*tr[lson].len)%mo;
tr[rson].sum=(tr[rson].sum+mark*tr[rson].len)%mo;
tr[rt].mark=0;
}
}
void modify(rg rt,rg L,rg R,ll x)
{
rg l=tr[rt].l,r=tr[rt].r;
if(L<=l&&r<=R)
{
tr[rt].sum=(tr[rt].sum+tr[rt].len*x)%mo;
tr[rt].mark+=x;
return;
}
pushdown(rt);
rg mid=l+r>>1;
if(L<=mid) modify(lson,L,R,x);
if(R>mid) modify(rson,L,R,x);
pushup(rt);
}
ll query(rg rt,rg L,rg R)
{
rg l=tr[rt].l,r=tr[rt].r;
if(L<=l&&r<=R) return tr[rt].sum;
pushdown(rt);
rg mid=l+r>>1;RG ll ret=0;
if(L<=mid) ret=(ret+query(lson,L,R))%mo;
if(R>mid) ret=(ret+query(rson,L,R))%mo;
return ret;
}
il ll asksum(rg u,rg v)
{
RG ll Ans=0;
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]]) swap(u,v);
Ans=(Ans+query(1,id[top[u]],id[u]))%mo;
u=fa[top[u]];
}
if(id[u]>id[v]) swap(u,v);
Ans=(Ans+query(1,id[u],id[v]))%mo;
return Ans;
}
il void addsum(rg u,rg v,ll x)
{
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]]) swap(u,v);
modify(1,id[top[u]],id[u],x);
u=fa[top[u]];
}
if(id[u]>id[v]) swap(u,v);
modify(1,id[u],id[v],x);
}
int main()
{
n=gi(),m=gi(),root=gi(),mo=gi();
for(rg i=1;i<=n;++i) w[i]=gi();
for(rg i=1,a,b;i<n;++i)
a=gi(),b=gi(),Eadd(a,b);
dfs1(root,0);
dfs2(root,root);
// pou_debug();
build(1,1,n);
// Seg_debug();
for(rg x,y,z,i=1;i<=m;++i)
{
opt=gi();
if(opt==1)
{
x=gi(),y=gi(),z=gi();
addsum(x,y,z);
}
if(opt==2)
{
x=gi(),y=gi();
printf("%lld\\n",asksum(x,y));
}
if(opt==3)
{
x=gi(),y=gi();
modify(1,id[x],id[x]+siz[x]-1,y);
}
if(opt==4)
{
x=gi();
printf("%lld\\n",query(1,id[x],id[x]+siz[x]-1));
}
}
return 0;
}Splay:
http://k-xzy.cf/archives/3251 (ztO 大佬XZY Orz)
就是一棵二叉搜索树为了平衡转来转去(平衡是为了保证查询修改操作复杂度优秀)
旋转的步骤理解了,代码就很容易理解
推荐一些资料
http://blog.csdn.net/qq_30974369/article/details/77587168
http://blog.csdn.net/u014634338/article/details/49586689
Splay的学习很耗草稿纸,但是画图真的很好理解
理解完旋转操作之后,代码就很好理解啦
https://www.luogu.org/problemnew/show/3391
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
#define ul unsigned long long
#define rg register int
#define ll long long
#define il inline
#define INF 2147483647
#define SZ 10000000
using namespace std;
struct SplayTree{
int ch[2],ff,son,cnt,val,mark;
}t[SZ];
int tot,root;
il void pushup(int u){ t[u].son=t[t[u].ch[0]].son+t[t[u].ch[1]].son+t[u].cnt; }
il void pushdown(int x){
if(t[x].mark){
t[ t[x].ch[0] ].mark ^= 1;
t[ t[x].ch[1] ].mark ^= 1;
t[x].mark = 0;
swap(t[x].ch[0] , t[x].ch[1]);
}
}
il void rotate(int x){
rg y = t[x].ff;
rg z = t[y].ff;
rg k = (x == t[y].ch[1]);
t[z].ch[ t[z].ch[1]==y ] = x; t[x].ff = z;
t[y].ch[k] = t[x].ch[k^1]; t[ t[x].ch[k^1] ].ff = y;
t[x].ch[k^1] = y; t[y].ff = x;
pushup(y) , pushup(x);
}
il void Splay(int x,int goal){
while( t[x].ff != goal ){
rg y = t[x].ff;
rg z = t[y].ff;
if(z != goal)
(t[y].ch[1] == x)^(t[z].ch[1] == y) ? rotate(x) : rotate(y);
rotate(x);
}
if(!goal) root = x;
}
il void insert(int x){
rg u = root,ff = 0;
while( (u) && (t[u].val!=x) ){
ff = u;
u = t[u].ch[ x>t[u].val ];
}
if( u ) ++t[u].cnt;
else{
u = ++tot;
if(ff) t[ff].ch[x>t[ff].val] = u;
t[u].son=t[u].ch[1]=t[u].ch[0]=0;
t[u].ff=ff,t[u].val=x,t[u].cnt=1;
}
Splay(u,0);
}
il int K_th(int x){
rg u = root;
if(t[u].son < x) return 0;
while(666){
pushdown(u);
rg y=t[u].ch[0];
if(x > t[y].son+t[u].cnt){
x -= t[y].son+t[u].cnt;
u = t[u].ch[1];
}
else if(x <= t[y].son) u=y;
else return t[u].val;
}
}
il void work(int l,int r){
l=K_th(l),r=K_th(r+2);
Splay(l,0);Splay(r,l);
t[ t[ t[root].ch[1] ].ch[0] ].mark ^= 1;
}
int n,m,l,r;
void ou(int u){
pushdown(u);
if(t[u].ch[0]) ou(t[u].ch[0]);
if((t[u].val>1) && (t[u].val<n+2)) printf("%d ",t[u].val-1);
if(t[u].ch[1]) ou(t[u].ch[1]);
}
int main(){
scanf("%d%d",&n,&m);
for(rg i = 1;i <= n+2;++i) insert(i);
while( m-- ){
scanf("%d%d",&l,&r);
work(l,r);
}
ou(root);
return 0;
}(怎么还没开始讲就已经写了这么多了)
真正的正文
LCT能干什么?
[下文摘自百度百科]
维护一个数据结构, 支持以下操作:
查询一个点的父亲
查询一个点所在的树的根
修改某个节点的权
向从某个节点到它所在的树的根的路径上的所有的节点的权增加一个数
查询从某个节点到它所在的树的根的路径上的所有的节点的权的最小值
把一棵树从某个节点和它的父亲处断开,使其成为两棵树
让一棵树的根成为另一棵树的某个节点的儿子,从而合并这两棵树
把某棵树的根修改为它的某个节点
查询在同一棵树上的两个节点的LCA
修改以某个节点为根的子树的所有节点的权
查询以某个节点为根的子树的所有节点的权的最小值
也就是,树链剖分能干的事情他基本能干,而且能够一边 修改连边情况 或 修改点权 一边干(不代表更容易实现)
那么我们继续学习操作
在学习操作之前有两条你是\\(必须必须必须\\)记住并且深刻理解
不要死在树链剖分的惯性思维里
\\[Splay维护的是一棵树上的深度\\]
\\[树、树根是可以变化的\\]
起初,上帝创造世界,造出了三个世界:现实世界、虚幻世界、Splay极乐世界
下面是初始情况
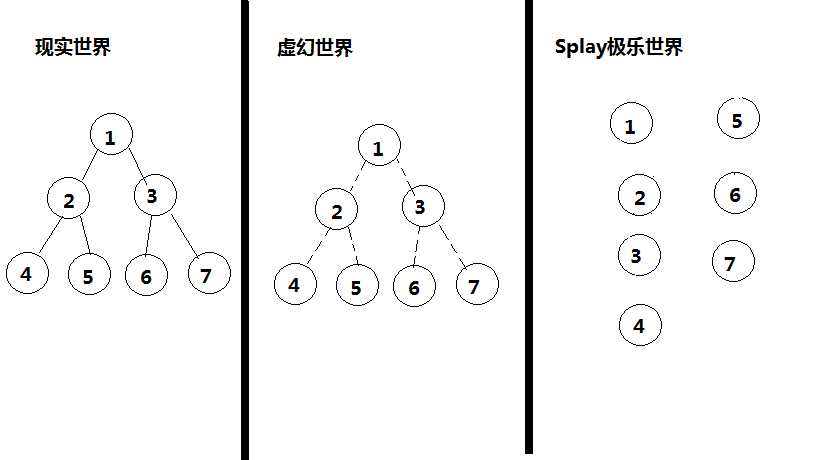
讲一下含义:
现实世界指我们所认识的树
虚幻世界指在Splay的连边情况(虚线代表现实中有连边但是Splay中无连边)
Splay极乐世界是为了方便理解,更加直观,把虚幻世界中的Splay抠出来形成一棵我们所熟悉的Splay(一定记住Splay维护的是一棵树上的深度)
可以由图看到一切的初始情况:现实世界有连边,Splay都是一个个孤立的点
特别的,对于现实世界的连边,我们不需要存一条条的边,而是利用我们已有的Splay构造边。
对于一条存在于现实世界,但是不存在于极乐世界的边1-2,其中1在\\(当前现实世界\\)的树的深度小于2,我们规定2记录有1这个父亲,而1却不记有这个儿子。
既存在于现实世界又存在于极乐世界的边里孩子认父亲,父亲也认孩子(美好的团圆)(也就是正常的Splay)
绝对不存在不存在于现实世界又存在于极乐世界的边(绕口)
这样连边有很大的好处:
①在极乐世界一个点pushup时由于父亲不认儿子所以不会被不在同一极乐世界树上的点影响
②保证了极乐世界树转换变形的便捷性,因为认不认儿子就可以使得转换
但是可以注意到有一个弊端
我们似乎不能通过一直向上找父亲的方法
区分一个点所在 现实世界树 和 极乐世界树 的树根。
因为两个找到的结果肯定都是一样的
所以根据子认父,父不认子的情况,我们构造一个函数isroot来判断当前点是不是极乐世界的splay的根
il bool isroot(rg x)
{
return tr[tr[x].fa].ch[0]!=x && tr[tr[x].fa].ch[1]!=x;
}很显然就不解释了
还有一个定义:\\(虚幻世界\\)中一段实链的深度必须是单调的,即不能出现4->2->5的情况(见下access操作的图)这保证了二叉搜索树的建成
access操作: (访问一个儿子)
5号点想要和1号点成为一棵Splay上的点(也就是在虚拟世界中以实边相连)
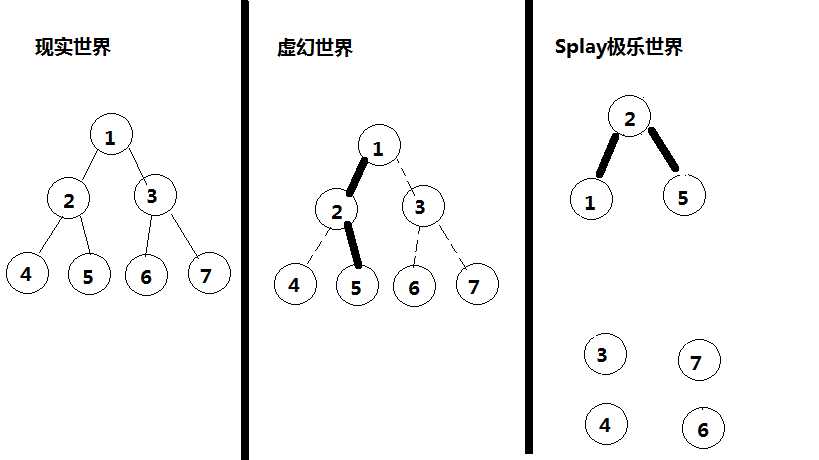
注意Splay维护的是深度
怎么办呢?
很简单,从5开始一直向上找父亲,然后让父亲转过头回来认儿子
注意
il void access(rg x)
{
for(rg y=0;x;y=x,x=tr[x].fa)
splay(x),tr[x].ch[1]=y,pushup(x);
}